Vienības aplis ir aplis, kura rādiuss ir 1. Vienības apļa centrs atrodas uz ass sākuma (0,0). The apkārtmērs Vienības apļa laukums ir 2π vienības, savukārt vienības apļa laukums ir π vienības2. Tam ir visas Circle īpašības. Vienības aplim ir vienādojums x2+ un2= 1. Šis vienību aplis palīdz definēt dažādus trigonometriskos jēdzienus.
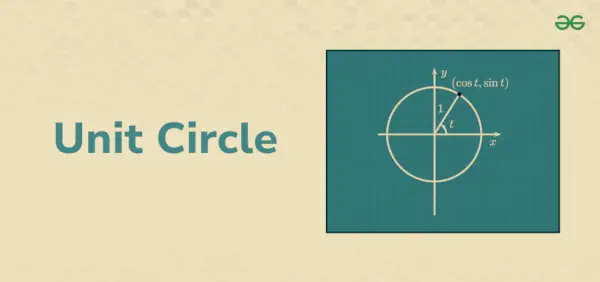
Vienības aplis
Vienības aplis bieži tiek apzīmēts kā S1vispārināšana uz augstākām dimensijām ir vienības sfēra. Tālāk sīkāk sapratīsim vairāk par vienību apli, formulu un atrisinātajiem piemēriem.
Kas ir vienības aplis?
Vienība Aplis ir aplis, kura rādiuss ir viena (1) vienība. Mēs izmantojam Dekarta plakni, lai uzzīmētu vienības apli, un vienības aplis ir 2 grādu polinoms ar diviem mainīgajiem. Vienības aplim ir dažādi pielietojumi trigonometrijā un algebrā, un to galvenokārt izmanto, lai atrastu dažādu trigonometrisko attiecību vērtības, piemēram, sin x, cos x, tan x un citas.
Vienības apļa definīcija
Matemātikā vienības apli mēs definējam kā fiksēta punkta lokusu, kas atrodas vienas vienības attālumā no apļa centra. Vienības apļa rādiuss ir vienas vienības rādiuss, un līdz ar to nosaukums vienības aplis.
Vienības apļa vienādojums
Mēs zinām, ka jebkura apļa vienādojums ar centru (h, k) un rādiusu “r” ir,
(x–h) 2 + (y–k) 2 = r 2
Vienības apļa gadījumā mēs zinām, ka r ir 1 vienība, un tāpēc vienības apļa vienādojums ir,
(x–h) 2 + (y–k) 2 = 1
Vienības apļa formula
Ja vienības apļa centrs ir izcelsme, t.i., (h, k) = (0, 0), tad vienības apļa vienādojums ir,
x 2 + un 2 = 1
Vienības aplis ir attēlots tālāk pievienotajā attēlā ar centra koordinātām h, k un, kad aplis atrodas sākuma punktā, h un k vērtība ir nulle un rādiuss AP ir vienāds ar 1 vienību.
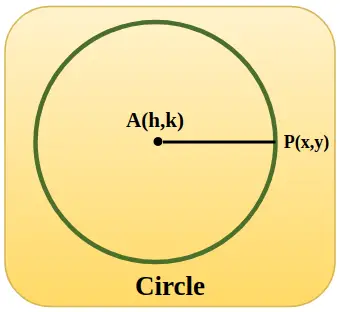
Trigonometriskās funkcijas, izmantojot vienību apli
Pitagora teorēmas pielietojumu vienības aplī var labāk izmantot, lai izprastu trigonometriskās funkcijas. Šim nolūkam mēs uzskatām, ka taisnleņķa trīsstūris ir novietots vienības aplī Dekarta koordinātu plaknē. Ja pamanām, šī apļa rādiuss apzīmē taisnleņķa trīsstūra hipotenūzu.
Apļa rādiuss veido vektoru. Tas noved pie leņķa veidošanās, piemēram, θ ar pozitīvo x asi. Pieņemsim, ka x ir attiecīgi taisnleņķa trijstūra bāzes garums un y ir augstuma garums. Arī rādiusa vektora galapunktu koordinātas ir attiecīgi (x, y).
Taisnleņķa trīsstūrī ir attiecīgi malas 1, x un y. Trigonometrisko attiecību tagad var aprēķināt šādi:
sin θ = augstums/hipotenūza = y/1
cos θ = Bāze/Hipotenūza = x/1
Tagad
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Aizstājot θ vērtības, mēs varam iegūt visu trigonometrisko funkciju galvenās vērtības. Līdzīgi tiek atrastas trigonometrisko funkciju vērtības dažādās vērtībās.
Vienības aplis ar Sin Cos un Tan
Jebkurš punkts uz vienības apļa ar koordinātām (x, y) tiek attēlots, izmantojot trigonometriskās identitātes kā, (cosθ, sinθ). Rādiusa stūru koordinātas attēlo θ vērtību kosinusu un sinusu konkrētai θ vērtībai un rādiusa līnijai. Mums ir cos θ = x un sin θ = y. Katrai apļa daļai ir četras daļas, kas atrodas vienā kvadrantā, veidojot 90°, 180°, 270° un 360° leņķi. Rādiusa vērtības ir attiecīgi no -1 līdz 1. Arī sin θ un cos θ vērtības ir attiecīgi no 1 līdz -1.
Vienības aplis un trigonometriskās identitātes
Vienības apļa trigonometriskās identitātes kotangensam, sekantam un kosekantam var aprēķināt, izmantojot sin, cos un tan identitātes. Noslēgumā mēs iegūstam taisnleņķa trīsstūri ar malām attiecīgi 1, x un y. Vienību apļa identitātes aprēķināšanu var izteikt kā,
- sin θ = y/1
- cos θ = x/1
- iedegums θ = y/x
- sek θ = 1/x
- cosec θ = 1/g
- bērnu gultiņa θ = x/y
Vienības apļa diagramma
Vienības apļa diagramma ir diagramma, kas satur trigonometriskās funkcijas sinusa un kosinusa vērtību dažādiem leņķiem. Vienības apļa diagramma tam pašam ir pievienota zemāk,
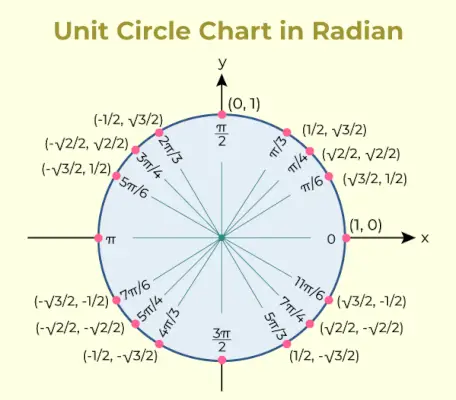
Vienības apļa tabula
Vienības apļa tabulā izmantotās trigonometriskās attiecības tiek izmantotas, lai uzskaitītu to punktu koordinātas uz vienības apļa, kas atbilst kopējiem leņķiem.
| Leņķi | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| bez | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| tātad | 0 | 1/√(3) | 1 | √(3) | Nav definēts |
| csc | Nav definēts | 2 | √(2) | 23) | 1 |
| sek | 1 | 23) | √(2) | 2 | Nav definēts |
| bērnu gultiņa | Nav definēts | √(3) | 1 | 1/√(3) | 0 |
Vienības apļa Pitagora identitātes
Ir trīs Pitagora identitātes, un tās visas ir viegli pierādīt, izmantojot vienības apļa koncepciju, kas ir trīs Pitagora identitātes,
- bez2θ + cos2θ = 1
- 1 + tā2θ = sek2i
- 1 + bērnu gultiņa2θ = cosec2i
Vienības apļa kompleksā plakne
Kompleksie skaitļi un kompleksā plakne ir viegli izskaidrojami, izmantojot vienības apļa jēdzienu. Vienības apļa vienādojums kompleksā formā ir:
|z| = 1
mia khalifa vecumsVAI
x 2 + un 2 = 1
Eilera formā kompleksais skaitlis tiek attēlots kā
z = e to = cos t + i (sin t)
Lasīt vairāk
Atrisināti piemēri par vienību apli
Q1: Pierādiet, ka punkts Q atrodas uz vienību apļa, Q = [1/√(6), √4/√6]
Risinājums:
Ņemot vērā,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Vienības apļa vienādojums ir,
x2+ un2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Tādējādi punkts Q[1/√(6), √4/√6] neatrodas uz vienības apļa.
Q2: Aprēķiniet līdz 30 O izmantojot vienības apļa sin un cos vērtības.
Risinājums:
iedegums 30°, izmantojot sin un cos vērtības,
iedegums 30° = (sin 30°)/ (cos 30°)
- bez 30° = 1/2
- cos 30° = √(3)/2
iedegums 30° = 1/2/√(3)/2
iedegums 30° = 1/√(3)
Q3: pārbaudiet, vai punkts P [1/2, √(3)/2] atrodas uz vienības apļa.
Risinājums:
Ņemot vērā,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Vienības apļa vienādojums ir,
- x2+ un2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Prakses jautājumi par vienību apli
Q1. Pārbaudiet, vai punkti A (1/2, 3/2) atrodas uz vienības apļa.
Q2. Pārbaudiet, vai punkti A (2, 1/2) atrodas uz vienības apļa.
Q3. Atrodiet cos 240° vērtību
Q4. Atrodiet iedeguma vērtību 320°
Q5. Atrodiet grēka vērtību 160°
Vienības aplis – FAQ
Kas ir vienības aplis?
Vienības aplis ir definēts kā punkta atrašanās vieta, kas atrodas vienas vienības attālumā no fiksēta punkta. Tā centrs atrodas (0,0), un tā rādiusa vērtība ir 1.
Kā pārbaudīt, vai punkts atrodas uz vienības apļa?
Jebkurš punkts, kas atrodas 2D plaknē un ir formā (x, y), tiek ievietots vienības apļa vienādojumā x2+ un2= 1, lai pārbaudītu, vai tas atrodas uz apļa vai nē.
Kāda ir vienības apļa formula?
Vienības apļa formula ir formula, ko izmanto, lai algebriski attēlotu vienības apli. Vienības apļa formula ir dota kā
x 2 + un 2 = 1
Kāpēc to sauc par vienības apli?
Vienības apli sauc par vienības apli, jo tā rādiuss ir viena (1) vienība.
