Trigonometrijas tabula ir standarta tabula, kas palīdz mums atrast trigonometrisko attiecību vērtības standarta leņķiem, piemēram, 0°, 30°, 45°, 60° un 90°. Tas sastāv no visām sešām trigonometriskajām attiecībām: sinusa, kosinusa, pieskares, kosekantu, sekantu un kotangensu.
Sīkāk uzzināsim par trigonometrijas tabulu.
Satura rādītājs
- Trigonometrijas tabula
- Trigonometrisko funkciju tabula
- Trigonometrisko attiecību apguve
- Kā iegaumēt trigonometrisko tabulu
- Kā izveidot trigu tabulu
- Trigonometriskās formulas
- Trigonometrisko identitāšu tabula
- Trigonometrisko tabulu piemēri
Trigonometrijas tabula
Trigonometriskā tabula ir visu sešu trigonometrisko funkciju vērtību izkārtojums to kopējiem leņķiem tabulas veidā.
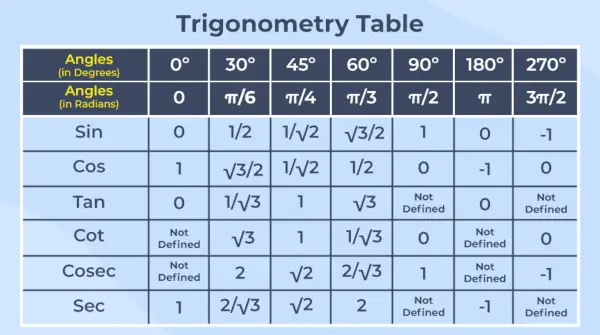
Piezīme – Trigonometrija ir matemātikas nozare, kas nodarbojas ar taisnleņķa trijstūra leņķu un malu attiecībām.
Trigonometrisko funkciju tabula
Trigonometrijai ir 6 trigonometriskās pamatfunkcijas, tās ir sinusa, kosinuss, tangenss, kosekants, sekants un kotangenss. Tagad apskatīsim trigonometriskās funkcijas.
Jebkuram taisnleņķa trīsstūrim ar perpendikulu (P), bāzi (B) un hipotenūzu (H), sešas trigonometriskās funkcijas ir šādas:
| Trigonometrisko funkciju tabula | |||
| Funkcija | Definīcija | Pārstāvība | Attiecības ar taisnleņķa trijstūra malām |
| Viņa | Perpendikula un hipotenūzas attiecība | bez i | Pretējā puse / hipotenūza |
| Kosinuss | Bāzes un hipotenūzas attiecība | cos i | Blakus puse / hipotenūza |
| Pieskares | Leņķa sinusa un kosinusa attiecība | tātad i | Pretējā puse / blakus puse |
| Kosekants | Grēka θ apgrieztā vērtība | csc i vai cosec i | Hipotenūza / pretējā puse |
| Sekants | Cos θ apgrieztā vērtība | sek i | Hipotenūza / blakus esošā puse |
| Kotangenss | Iedeguma θ reciproks | bērnu gultiņa i | Blakus puse / pretējā puse |
Piezīme - Trigonometrija ir matemātikas nozare, kas nodarbojas ar attiecībām starp trijstūra leņķiem un malām, īpaši taisnleņķa trijstūriem. Tas ietver sinusa, kosinusa, tangensu un citu trigonometrisko funkciju izpēti un pielietošanu, lai atrisinātu problēmas dažādās jomās.
Pārbaudiet : Trigonometrija: formulas, tabula, identitātes un attiecības
Trigonometrisko attiecību apguve
Izpētiet tālāk apskatīto tabulu, lai viegli iegaumējamā veidā uzzinātu trigonometriskās attiecības.
| Dažiem cilvēkiem ir cirtaini melni mati, lai radītu skaistumu |
| sin θ (daži) = perpendikulāri (cilvēki) / hipotenūza (ir) |
| cos θ (cirtaini) = pamatne (melna) / hipotenūza (mati) |
| iedegums θ (līdz) = perpendikulārs (ražot) / bāze (skaistums) |
Kā iegaumēt trigonometrisko tabulu
Trigonometrijas tabulu ir diezgan viegli atcerēties, ja zināt visas trigonometrijas formulas. Ir arī triks, ko sauc par vienas rokas triks lai iegaumētu trigonometrijas tabulu.

1. darbība: Iepriekš redzamajā attēlā sinusa tabulai saskaitiet pirkstus kreisajā pusē standarta leņķim.
2. darbība: Sadaliet pirkstu skaitu kreisajā pusē (aprēķiniet 1. solī) ar 4
3. darbība: Atrodiet 2. darbībā aprēķinātās vērtības kvadrātsakni.
Pārbaudiet: Trigonometrijas formulas — visu trigonometrisko identitāšu un formulu saraksts
Kā izveidot trigu tabulu
Izpētiet tālāk norādītās darbības, lai izveidotu trigonometrisko tabulu standarta leņķiem.
1. darbība: izveidojiet tabulu
Izveidojiet tabulu un uzskaitiet visus leņķus, piemēram 0°, 30°, 45°, 60° un 90°, augšējā rindā. Pirmajā kolonnā ievadiet visas trigonometriskās funkcijas sin, cos, tan, cosec, sec un cot.
2. darbība. Novērtējiet vērtību visiem grēka funkcijas leņķiem.
Lai atrastu grēka funkcijas vērtības, sadaliet 0, 1, 2, 3 un 4 ar 4 un ņemiet katras vērtības saknē attiecīgi kā:
Par vērtību sin 0° = √(0/4) = 0
Līdzīgi,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1
| bez 0° | bez 30° | bez 45° | bez 60° | bez 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
3. darbība: Novērtējiet vērtību visiem cos funkcijas leņķiem
Funkcijas cos vērtība ir pretēja sin funkcijas vērtībai, t.i., cos 0° = sin 90°, cos 30° = sin 60° un cos 45° = sin 45°, tātad
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
4. darbība. Novērtējiet vērtību visiem iedeguma funkcijas leņķiem
Tan funkcijas vērtība ir vienāda ar sin funkciju, kas dalīta ar cos funkciju, t.i., tan x = sin x / cos x. Visu leņķu vērtību iedeguma funkcijā aprēķina šādi:
iedegums 0°= sin 0° / cos 0° = 0/1 = 0, līdzīgi
| tātad 0° | tātad 30° | tātad 45° | tātad 60° | tātad 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Nav definēts |
5. darbība. Novērtējiet visu cosec funkcijas leņķu vērtību
Cosec funkcijas vērtība ir vienāda ar grēka funkcijas apgriezto vērtību. Cosec 0° vērtību iegūst, ņemot sin 0° apgriezto vērtību
cosec 0° = 1 / sin 0° = 1 / 0 = nav definēts. Līdzīgi,
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| Nav definēts | 2 | √2 | 23 | 1 |
6. darbība. Novērtējiet visu sec funkcijas leņķu vērtību
java noklusējuma parametri
Funkcijas sec vērtība ir vienāda ar funkcijas cos apgriezto vērtību. Sec 0° vērtību iegūst, ņemot cos 0° apgriezto vērtību
sec 0° = 1 / cos 0° = 1 / 1 = 1. Līdzīgi,
| sek 0° | sec 30° | sec 45° | sec 60° | sec 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Nav definēts |
7. darbība. Novērtējiet vērtību visiem gultiņas funkcijas leņķiem
Bērnu gultiņas funkcijas vērtība ir vienāda ar iedeguma funkcijas apgriezto vērtību. Bērnu gultiņa 0° vērtību iegūst, ņemot tan 0° apgriezto vērtību
bērnu gultiņa 0° = 1 /iedegums 0° = 1 / 0 = Nav definēts. Līdzīgi,
| gultiņa 0° | gultiņa 30° | gultiņa 45° | gultiņa 60° | gultiņa 90° |
|---|---|---|---|---|
| Nav definēts | √3 | 1 | 1/√3 | 0 |
Tādā veidā mēs varam izveidot šādu trigonometrisko attiecību tabulu:
| Grādi un radiāni trigonometriskā tabula | |||||||
|---|---|---|---|---|---|---|---|
| Leņķis (grādos) | Leņķis (radiānos) | Bez | Cos | Tātad | Cosec | Sec | Bērnu gultiņa |
| 0° | 0 | 0 | 1 | 0 | nenoteikts | 1 | nenoteikts |
| 30° | p/6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | nenoteikts | 1 | nenoteikts | 0 |
Trigonometriskās formulas
Uzzināsim par dažām trigonometrijas formulām, kas saistītas ar papildu un papildu leņķiem.
- Papildu leņķi: Leņķu pāris, kuru summa ir vienāda ar 90°
- Papildu leņķi: Leņķu pāris, kuru summa ir vienāda ar 180°
Pārbaudiet: Trigonometriskās attiecības
Papildu leņķu trigu identitātes
Papildu leņķu identitātes ir balstītas uz attiecību starp divu leņķu trigonometriskajām funkcijām, kuru summa ir 90 grādi (vai π/2 radiāni). Tie ir pazīstami kā kopfunkciju identitātes .
| Trigonometriskā funkcija | Identitāte |
|---|---|
| Viņa | sin(90°− i )=cos i |
| Kosinuss | cos(90°− i )=bez i |
| Pieskares | iedegums(90°− i )=gultiņa i |
| Kotangenss | gultiņa (90°− i )=tātad i |
| Sekants | sec(90°− i )=csc i |
| Kosekants | cosec(90°− i )=sek i |
Papildu leņķu trigu identitātes
Papildu leņķu identitātes attiecas uz divu leņķu trigonometriskajām funkcijām, kuru summa ir 180 grādi (vai π radiāni).
| Trigonometriskā funkcija | Identitāte |
|---|---|
| Viņa | sin(180°− i )=bez i |
| Kosinuss | cos(180°− i )=-cos i |
| Pieskares | iedegums(180°− i )=−iedegums i |
| Kotangenss | gultiņa (180°− i )=− gultiņa i |
| Sekants | sek(180°− i )=−sek i |
| Kosekants | cosec(180°− i )=cosec i |
Trigonometrisko identitāšu tabula
Trigonometriskās identitātes ir identitātes, kuras plaši izmanto trigonometrisko problēmu risināšanā. Ir dažādas trigonometriskās identitātes, bet trīs galvenās trigonometriskās identitātes ir:
| Trigonometrisko identitāšu tabula | |
| Trigonometriskā identitāte | Formula |
| Pitagora identitāte | bez2θ + cos2θ = 1 |
| Sekanta-Tangenta identitāte | sek2θ – tātad2θ = 1 |
| Kosekanta-kotangentes identitāte | cosec2θ – bērnu gultiņa2θ = 1 |
Pārbaudiet arī:
- Trigonometriskās attiecības
- Apgrieztās trigonometriskās identitātes
- Augstumi un attālumi
Trigonometrisko tabulu piemēri
Atrisināsim dažus jautājumus trigonometriskajā tabulā.
1. piemērs: ja sin θ = 4/5, tad atrodiet visas trigonometriskās vērtības.
Risinājums:
Šeit mums ir,
sin θ = 4/5
kā, sin θ = perpendikulārs / hipotenūza
tātad mums ir perpendikuls (P) = 4 un hipotenūza (H) = 5
Tātad saskaņā ar Pitagora teorēmu H 2 = P 2 +B 2
Noskaidrosim bāzes (B) vērtību
52= B2+ 42
25 = B2+ 16
25–16 = B2
B2= 9
B = 3Tagad mums ir,
Sin θ = perpendikulārs/hipotenūza
= AB/AC = 4/5Kosinuss θ = bāze/hipotenūza
= BC/AC = 3/5Pieskares θ = perpendikulārs/bāze
= AB/BC = 4/3Kosekants θ = hipotenūza/perpendikulārs
= AC/AB = 5/4Sekants θ = hipotenūza/bāze
= AC/BC = 5/3Kotangente θ = bāze/perpendikula
= BC/AB = 3/4
2. piemērs. Atrodiet vērtību cos 45° + 2 sin 60° – tan 60°.
Risinājums:
No trigonometrijas tabulas
cos 45° = 1/√2, sin 60° = √3/2 un iedegums 60° = √3
Tādējādi
cos 45° + 2 sin 60° – iedegums 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
3. piemērs. Atrodiet cos 75° vērtību.
Risinājums:
Mēs to zinām,
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Secinājums – trigonometrijas tabula
Trigonometrijas tabula sniedz visaptverošu atsauci par trigonometriskajām funkcijām sinusu, kosinusu, tangensu, kosekantu, sekantu un kotangensu, kā arī to attiecīgās vērtības dažādiem leņķiem. es t kalpo kā vērtīgs līdzeklis risināšanai trigonometriskie vienādojumi, ģeometrisko attiecību analīze un periodisku parādību uzvedības izpratne. Vai iekšā matemātikā, fizikā, inženierzinātnēs vai citās jomās, trigonometrijas tabula palīdz aprēķinos, problēmu risināšanā un vizualizācijā, palīdzot dziļāk izprast trigonometriskos jēdzienus un to pielietojumus reālās pasaules scenārijos.
Trigonometrijas tabula — FAQ
Kas ir trigonometrija?
Trigonometrija ir matemātikas nozare, kas nodarbojas ar jebkura trijstūra leņķi un malām.
Kas ir trigonometriskā tabula?
Trigonometrijas tabula ir tabula, kurā ir visu sešu kopējo leņķu trigonometrisko funkciju vērtības.
Kurš izgudroja trigonometrijas tabulu?
Grieķu astronoms Hiparhs (127. g. pmē.) izgudroja trigonometrijas tabulu.
Kas ir standarta leņķi trigonometriskajā tabulā?
Standarta leņķi trigonometriskajā tabulā ir 0°, 30°, 45°, 60° un 90°
Kāda ir iedeguma vērtība 45 grādi?
Iedeguma 45 grādu vērtība ir 1.
Kā iemācīties trigonometrijas tabulu?
Trigonometriskās tabulas apguves triks ir:
- Jums ir jāapgūst visas grēka funkcijas leņķu vērtības.
- Visu cos funkcijas leņķu vērtība ir sin funkcijas spoguļattēls.
- Tan funkcijas vērtības var aprēķināt, dalot sin funkciju ar cos funkciju.
- Cosec funkcijas vērtība ir grēka abpusēja.
- Līdzīgi sec un cot ir savstarpēji saistīti ar cos un cot funkciju.
Kādas ir sešas pamatfunkcijas trigonometriskajā tabulā?
Sešas trigonometriskās pamatfunkcijas trigonometriskajā tabulā ir sinuss, kosinuss, tangenss, sekants, kotangenss un kosekants.
Vai ir kalkulatori, kas var aizstāt trigonometrijas tabulas?
Zinātniskie kalkulatori var aprēķināt trigonometriskās attiecības jebkuram leņķim8.
Kāda ir trigonometrijas tabulas izmantošana?
Trigonometrijas tabulu pamatā izmanto, lai atrastu visu trigonometrisko attiecību vērtības visiem leņķiem. Šīm vērtībām ir vairākas reālās dzīves pielietošanas iespējas.
