Kompleksie skaitļi ir dabisks reālu skaitļu turpinājums. Mūsdienu laikmetā kompleksos skaitļus izmanto daudzās jomās, piemēram, ciparu signālu apstrādē, kriptogrāfijā un daudzās ar datoru saistītās jomās.

Šajā rakstā mēs uzzināsim par iedomātiem skaitļiem, kompleksajiem skaitļiem un to veidiem, dažādām operācijām ar kompleksajiem skaitļiem, komplekso skaitļu īpašībām, komplekso skaitļu pielietojumu utt.

Komplekso skaitļu definīcija

Kompleksie skaitļi ir cipariem no formas (a + i b) kur a & b ir reālie skaitļi un i ir iedomāta vienība, ko sauc par iota, kas apzīmē √-1. Piemēram, 2 + 3i ir komplekss skaitlis, kurā 2 ir reāls skaitlis un 3i ir iedomāts skaitlis. Kompleksos skaitļus var uzrakstīt kā a + ib, kur a un b ir racionāli skaitļi, kurus var attēlot uz skaitļu līnijas, kas stiepjas līdz bezgalība .

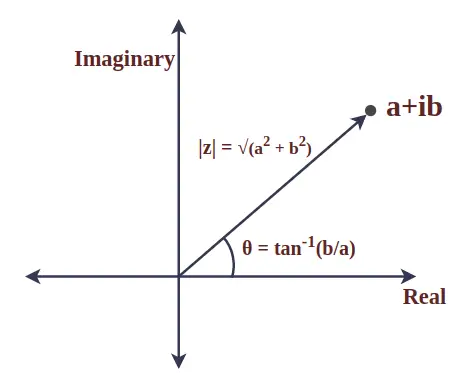
Kompleksā skaitļa modulis

Kompleksā skaitļa modulis ir absolūtā vērtība un atspoguļo attālumu starp sākumpunktu un doto punktu. To sauc arī par kompleksā skaitļa lielumu. Apskatīsim komplekso skaitli z = a + ib, tad z modulis tiek definēts šādi:

|z| = √(a ² + b ² )

kur,

• a ir kompleksā skaitļa z reālā daļa, un
• b ir kompleksā skaitļa z iedomātā daļa.

Kompleksā skaitļa arguments

Leņķi starp kompleksā skaitļa rādiusa vektoru un pozitīvo x asi sauc par kompleksā skaitļa argumentu. Kompleksam skaitlim z = a + ib to matemātiski nosaka:

θ = iedegums ^-1 (ba)

kur,

• a ir kompleksā skaitļa z reālā daļa, un
• b ir kompleksā skaitļa z iedomātā daļa.

i (iota) spēks

I (iota) ir definēta kā kvadrātsakne no -1. Tādējādi jebkuru i jaudu var izteikt kā atkārtotu i reizinājumu ar sevi, t.i.,

• i = √(-1)
• i²= -1
• i³= – i
• i⁴= 1
• i⁵= i
• i⁶= – 1
• un tā tālāk..

Nepieciešamība pēc sarežģītiem skaitļiem

Senatnē cilvēki zināja tikai par naturāliem skaitļiem cipariem ir visintuitīvākie, jo cilvēka smadzenes jau tos saprot, izmantojot vizuālos attēlus, piemēram, aitas un pārtiku. Tādējādi mums ir tikai naturālo skaitļu kopa ( N ), bet naturālajos skaitļos nav atrisinājuma vienādojumam x + a = b (a> b) un a, b ∈ N. Tādējādi radās naturālu skaitļu paplašinājums, t.i., veseli skaitļi( es ).

Tagad atkal šajā skaitļu kopā nav atrisinājuma vienādojumam ax = b (a ≠ 0) un a, b ∈ I, kur a un b abi ir veseli skaitļi. Tādējādi veselu skaitļu kopa (I) tiek paplašināta līdz racionālu skaitļu kopai ( J ).

Atkal šajā racionālo skaitļu kopā nav vienādojuma x atrisinājuma²= a (a> 0) un a ∈ Q. Tādējādi, J tiek paplašināts, iekļaujot tādus skaitļus, ka x²= a(ja> 0), t.i., iracionāli skaitļi. Šīs kopas nosaukums ir Reālie skaitļi, un to attēlo R .

Tagad ilgu laiku tika uzskatīts, ka mums nav jāpaplašina šī reālo skaitļu kopa, lai izveidotu vēl vienu lielāku kopu, jo šī skaitļu kolekcija šķiet pabeigta. Bet atkal šajā skaitļu kopā radās jauna problēma, t.i., nav tāda reāla skaitļa, ka x²= a (a <0) un a ∈ R. Tādējādi reālo skaitļu kopa tiek paplašināta, lai iekļautu visus šādus skaitļus un nosauktus par kompleksajiem skaitļiem, un to attēlo ar C .

Komplekso skaitļu klasifikācija

Kā mēs zinām, kompleksā skaitļa standarta forma ir z = (a + i b) kur a, b ∈ R un i ir iota (iedomāta vienība). Tātad atkarībā no a (ko sauc par reālo daļu) un b (ko sauc par iedomāto daļu) vērtībām kompleksos skaitļus iedala četros veidos:

• Nulles kompleksais skaitlis
• Tīri reāli skaitļi
• Tīri iedomāti skaitļi
• Iedomātie skaitļi

Sīkāk uzzināsim par šiem veidiem.

Nulles kompleksais skaitlis

Jebkuram kompleksajam skaitlim z = a + ib, ja a = 0 & b = 0, tad komplekso skaitli sauc par nulles komplekso skaitli. Piemēram, vienīgais piemērs ir 0.

Tīri reāli skaitļi

Jebkuram kompleksajam skaitlim z = a + ib, ja a ≠ 0 & b = 0, tad komplekso skaitli sauc par tīri reālu skaitli, t.i., skaitli bez iedomātas daļas. Visi reālie skaitļi ir piemēri, piemēram, 2, 3, 5, 7 utt.

Tīri iedomāti skaitļi

Jebkuram kompleksajam skaitlim z = a + ib, ja a = 0 & b ≠ 0, tad komplekso skaitli sauc par tīri iedomātu skaitli, t.i., skaitli bez reālās daļas. Visi skaitļi bez reālām daļām ir šāda veida skaitļu piemēri, t.i., -7i, -5i, -i, i, 5i, 7i utt.

Iedomātie skaitļi

Jebkuram kompleksajam skaitlim z = a + ib, ja a ≠ 0 & b ≠ 0, tad komplekso skaitli sauc par iedomāts skaitlis . Piemēram, (-1 – i), (1 + i), (1 – i), (2 + 3i) utt.

Dažādas komplekso skaitļu formas

Ir dažādas komplekso skaitļu formas, kas ir,

• Taisnstūra forma
• Polārā forma
• Eksponenciālā forma

Tagad uzzināsim par tiem sīkāk.

Taisnstūra forma

Taisnstūra forma ir ko sauc arī par Standarta forma un to pārstāv (a + ib), kur a un b ir reālie skaitļi.

Piemēram: (5 + 5i), (-7i), (-3 – 4i) utt.

Polārā forma

Polārā forma ir kompleksa skaitļa attēlojums, kur polārās koordinātas [kur koordinātas ir attēlotas kā (r, θ), kur r ir attālums no sākuma un θ ir leņķis starp līniju, kas savieno punktu un sākumu, un pozitīvo x asi) tiek izmantoti, lai attēlotu kompleksu skaitu. Jebkurš kompleksais skaitlis tiek attēlots kā r [cos θ + i sin θ].

Piemēriem: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] utt.

Eksponenciālā forma

Komplekso skaitļu eksponenciālās formas ir komplekso skaitļu attēlojums, izmantojot Eilera formulu, un šajā formā kompleksais skaitlis tiek attēlots ar reⁱ, kur r ir punkta attālums no sākuma un θ ir leņķis starp pozitīvo x asi un rādiusa vektoru.

Piemēriem: eⁱ⁽⁰⁾, Tas ir^i(π/2), 5.e^i(π/6)utt.

Piezīme: Visas trīs iepriekš apskatītās komplekso skaitļu formas ir savstarpēji konvertējamas, t.i., tās var ļoti viegli pārvērst no vienas formas citā.

Operācijas ar kompleksajiem skaitļiem

Ar kompleksajiem skaitļiem var veikt šādas darbības:

• Papildinājums
• Atņemšana
• Reizināšana
• Divīzija
• Konjugācija

Komplekso skaitļu pievienošana

Mēs varam pievienot divus kompleksos skaitļus, vienkārši pievienojot to reālo un iedomāto daļu atsevišķi.

Piemēram, (3 + 2i) + (1 + 4i) = 4 + 6i.

Komplekso skaitļu atņemšana

Mēs varam atņemt divus kompleksos skaitļus, vienkārši atsevišķi atņemot to reālās un iedomātās daļas.

Piemēram, (3 + 2i) – (1 + 4i) = 2 – 2i.

Komplekso skaitļu reizināšana

Mēs varam reizināt divus kompleksos skaitļus, izmantojot sadalījuma īpašību un to, ka i²= -1.

Piemēram, (3 + 2i) (1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Komplekso skaitļu dalījums

Mēs varam dalīt vienu komplekso skaitli ar citu, vienkārši reizinot gan skaitītāju, gan saucēju ar saucēja komplekso konjugātu un vēl vairāk vienkāršojot izteiksmi.

Piemēram, (3 + 2i)/(1 + 4i) = (3 + 2i) (1–4i)/(1 + 4i) (1–4i) = (11–10i)/17.

Komplekso skaitļu konjugācija

Mēs varam viegli atrast kompleksa skaitļa konjugāts, vienkārši mainot tās iedomātās daļas zīmi. Kompleksā skaitļa konjugāts bieži tiek apzīmēts ar joslu virs skaitļa, piemēram, z̄.

Piemēram, 3 + 2i konjugāts ir 3 – 2i.

Sarežģītu skaitļu identitātes

Jebkuriem diviem kompleksajiem skaitļiem z₁un z₂var norādīt šādas algebriskās identitātes:

• (Ar ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (Ar ₁ - Ar ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (Ar ₁ ) ² - (ar ₂ ) ² = (z ₁ + z ₂ )(Ar ₁ - Ar ₂ )
• (Ar ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² Ar ₂ +3(z ₂ ) ² Ar ₁ + (z ₂ ) ³
• (Ar ₁ - Ar ₂ ) ³ = (z ₁ ) ³ – 3 (z ₁ ) ² Ar ₂ +3(z ₂ ) ² Ar ₁ - (ar ₂ ) ³

Formulas, kas saistītas ar kompleksajiem skaitļiem

Ir dažas formulas, kas saistītas ar kompleksajiem skaitļiem, no kurām dažas ir šādas:

Eilera formula

Eilera formula parāda attiecību starp eksponenta iedomāto jaudu un trigonometrisko attiecību sin un cos, un to nosaka:

Tas ir ^ix = cos x + i sin x

De Moivre formula

De Moivre formula izsaka n^thkompleksā skaitļa jauda polārā formā, un to nosaka:

java ja vēl

(cos x + i sin x) ⁿ = cos(nx) + i sin(nx)

Sarežģīta plakne

Plakni, kurā kompleksie skaitļi ir unikāli attēloti, sauc par komplekso plakni vai Arganda plakni vai Gausa plakni.

Kompleksajai plaknei ir divas asis:

• X ass vai reālā ass
• Y ass vai iedomātā ass

X ass vai reālā ass

• Visi tīri reālie kompleksie skaitļi ir unikāli attēloti ar punktu uz tā.
• Visu komplekso skaitļu reālā daļa Re(z) tiek uzzīmēta attiecībā pret to.
• Tāpēc tiek saukta arī X-ass Reālā ass .

Y ass vai iedomātā ass

• Visi tīri iedomātie kompleksie skaitļi ir unikāli attēloti ar punktu uz tā.
• Visu komplekso skaitļu iedomātā daļa Im(z) tiek uzzīmēta attiecībā pret to.
• Tāpēc arī Y-asi sauc Iedomātā ass .

Komplekso skaitļu ģeometriskā attēlošana

Kā zināms, katrs kompleksais skaitlis (z = a + i b) tiek attēlots ar unikālu punktu p(a, b) kompleksajā plaknē un katrs kompleksās plaknes punkts ir unikāls kompleksais skaitlis.

Lai attēlotu jebkuru komplekso skaitli z = (a + i b) kompleksajā plaknē, ievērojiet šīs vienošanās:

• Z reālā daļa (Re(z) = a) kļūst par punkta p X koordinātu

• z iedomātā daļa (Im(z) = b) kļūst par punkta p Y koordinātu

Un visbeidzot z (a + i b) ⇒ p (a, b), kas ir punkts kompleksajā plaknē.

Komplekso skaitļu īpašības

Ir dažādas komplekso skaitļu īpašības, no kurām dažas ir šādas:

• Jebkuram kompleksam skaitlim z = a + ib, ja z = 0, tad a = 0, kā arī b = 0.
• 4 reāliem skaitļiem a, b, c un d, lai z₁= a + ib un z₂= c + id. Ja z₁= z₂tad a = c un b = d.
• Saskaitot kompleksu skaitu ar tā konjugātu, tiek iegūts tīri reāls skaitlis, t.i., z + z̄ = reālais skaitlis.

Lai z = a + ib,

z + z̄ = a + viens + a – viens

⇒ z + z̄ = 2a (kas ir tīri reāls)

• Kompleksā skaitļa reizinājums ar tā konjugācijas rezultātiem ir arī tīri reāls skaitlis, t.i., z × z̄ = reālais skaitlis

Lai z = a + ib, tad

z × z̄ = (a + viens) × (a – viens)

⇒ z × z̄= a²– i²b²

⇒ z × z̄ = a²+ b²(kas ir tīri reāls)

• Kompleksie skaitļi ir komutatīvais saskaitīšanas un reizināšanas operācijā. Apskatīsim divus kompleksos skaitļus z₁un z₂, un tad

Ar ₁ +z ₂ = z ₂ +z ₁

Ar ₁ × z ₂ = z ₂ × z ₁

• Kompleksie skaitļi ir asociatīvs ar saskaitīšanas un reizināšanas operāciju. Apskatīsim trīs kompleksos skaitļus z₁, Ar₂, un z₃tad

(Ar ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Ar ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Sarežģītie skaitļi satur sadales īpašums reizināšanas ar saskaitīšanu, kā arī. Apskatīsim trīs kompleksos skaitļus z₁, Ar₂, un z₃tad

Ar ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Lasīt vairāk,

• Sarežģītu skaitļu dalīšana
• Z josla kompleksajos skaitļos

Komplekso skaitļu piemēri

1. piemērs. Uzzīmējiet šos kompleksos skaitļus z = 3 + 2i kompleksajā plaknē.

Risinājums:

Ņemot vērā:

Ar = 3 + 2 i

Tātad punkts ir z(3, 2). Tagad mēs attēlojam šo punktu zemāk esošajā grafikā, šajā grafikā x ass apzīmē reālo daļu un y ass apzīmē iedomāto daļu.

2. piemērs. Uzzīmējiet šos kompleksos skaitļus z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) kompleksajā plaknē.

Risinājums:

Ņemot vērā:

Ar₁= (2 + 2 i)

Ar₂= (-2 + 3 i)

Ar₃= (-1–3 i)

Ar₄= (1–i)

Tātad punkti ir z₁(2, 2), z₂(-2, 3), z₃(-1, -3) un z₄(1, -1). Tagad mēs attēlojam šos punktus zemāk esošajā grafikā, šajā grafikā x ass apzīmē reālo daļu un y ass apzīmē iedomāto daļu.

Bieži uzdotie jautājumi par kompleksajiem skaitļiem

Definējiet kompleksos skaitļus.

Skaitļus formā a+ib sauc par kompleksajiem skaitļiem, kur a un b ir reālais skaitlis un i ir iedomātā vienība, kas apzīmē kvadrātsakni no -1.

Kāda ir atšķirība starp reālo skaitli un komplekso skaitli?

Atšķirība starp reāliem un kompleksajiem skaitļiem ir tāda, ka mums ir nepieciešams tikai viens skaitlis, lai attēlotu jebkuru reālu skaitli, bet ir nepieciešami divi reāli skaitļi, lai attēlotu jebkuru komplekso skaitli.

Kāda ir kompleksā skaitļa reālā un iedomātā daļa?

Kompleksā skaitļā a + ib a ir kompleksā skaitļa reālā daļa, un b tiek saukta par kompleksā skaitļa iedomāto daļu.

Kas ir kompleksā skaitļa kompleksais konjugāts?

Kompleksam skaitlim a + ib a – ib sauc par tā komplekso konjugātu. Sarežģītus konjugātus var atrast, vienkārši mainot iedomātās daļas zīmi.

Kāds ir kompleksā skaitļa modulis?

Attālumu starp sākumpunktu un punktu, ko attēlo komplekss skaitlis arganda plaknē, sauc par šī pilnā skaitļa moduli, un z = a + ib to matemātiski nosaka:

|z| = √(a ² + b ² )

Kāds ir kompleksā skaitļa arguments?

Leņķi starp kompleksā skaitļa rādiusa vektoru un pozitīvo x asi sauc par kompleksā skaitļa argumentu, un, ja z = a + ib, to matemātiski nosaka:

θ = iedegums ^-1 (ba)

string to itn

Kāda ir kompleksā skaitļa polārā forma?

Jebkuram kompleksam skaitlim, z = a + ib, tā polāro formu nosaka:

r [cos θ + i sin θ]

Kas ir Eilera formula?

Eilera formula parāda attiecību starp eksponenta iedomāto jaudu un trigonometrisko attiecību sin un cos, un to nosaka:

Tas ir ^ix = cos x + i sin x