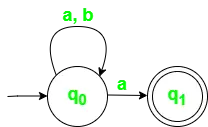
Finite Automata(FA) ir vienkāršākā iekārta modeļu atpazīšanai. To izmanto, lai raksturotu parasto valodu, piemēram: /baa+!/.
To izmanto arī, lai analizētu un atpazītu dabiskās valodas izteiksmes. Ierobežotais automāts jeb ierobežotā stāvokļa mašīna ir abstrakta mašīna, kurai ir pieci elementi jeb koreži. Tam ir stāvokļu un noteikumu kopums, lai pārietu no viena stāvokļa uz otru, taču tas ir atkarīgs no lietotā ievades simbola. Pamatojoties uz stāvokļiem un noteikumu kopu, ievades virkni var pieņemt vai noraidīt. Būtībā tas ir abstrakts digitālā datora modelis, kas nolasa ievades virkni un maina tā iekšējo stāvokli atkarībā no pašreizējā ievades simbola. Katrs automāts definē valodu, t.i., virkņu kopu, ko tas pieņem. Nākamajā attēlā parādītas dažas vispārējās automatizācijas galvenās iezīmes.
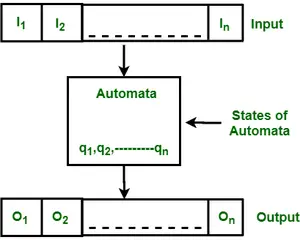
Attēls: Finite Automata iezīmes
Iepriekš redzamajā attēlā parādītas šādas automātu funkcijas:
- Ievade
- Izvade
- Automātu stāvokļi
- Valsts attiecības
- Izejas attiecība
Ierobežotais automāts sastāv no šādiem elementiem:
Q : Finite set of states. ? : set of Input Symbols. q : Initial state. F : set of Final States. ? : Transition Function.>
Mašīnas formālā specifikācija ir
{ Q, ?, q, F, ? }> FA iedala divos veidos:
1) Deterministiskie galīgie automāti (DFA):
DFA consists of 5 tuples {Q, ?, q, F, ?}. Q : set of all states. ? : set of input symbols. ( Symbols which machine takes as input ) q : Initial state. ( Starting state of a machine ) F : set of final state. ? : Transition Function, defined as ? : Q X ? -->J.> DFA konkrētai ievades rakstzīmei iekārta pāriet tikai uz vienu stāvokli. Pārejas funkcija ir definēta katrā stāvoklī katram ievades simbolam. Arī DFA nulles (vai ?) pārvietošana nav atļauta, t.i., DFA nevar mainīt stāvokli bez ievades rakstzīmes.
Piemēram, izveidojiet DFA, kas pieņem valodu, kurā ir visas virknes, kas beidzas ar “a”.
Ņemot vērā: ? = {a,b}, q = {q0}, F={q1}, Q = {q0, q1}
Vispirms apsveriet visu iespējamo pieņemamo virkņu valodu kopu, lai izveidotu precīzu stāvokļa pārejas diagrammu.
L = {a, aa, aaa, aaaa, aaaaa, ba, bba, bbba, tēvs, tēvs, tēvs, tēvs}
Iepriekš ir vienkārša iespējamo pieņemamo virkņu apakškopa, var būt arī daudzas citas virknes, kas beidzas ar “a” un satur simbolus {a,b}.
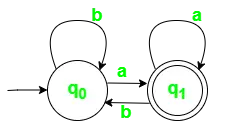
1. attēls. DFA stāvokļa pārejas diagramma ar ? = {a, b}
Nepieņemtās virknes ir,
ab, bb, aab, abbb utt.
java ja vēl
Stāvokļa pārejas tabula iepriekšējam automātam,
| ?ValstsSimbols? | a | b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q0 |
Viena svarīga lieta, kas jāņem vērā, ir, modelim var būt daudz iespējamo DFA . Parasti priekšroka tiek dota DFA ar minimālu stāvokļu skaitu.
2) Nedeterminēti ierobežotie automāti (NFA): NFA ir līdzīga DFA, izņemot šādas papildu funkcijas:
- Ir atļauta nulles (vai ?) kustība, t.i., tā var virzīties uz priekšu, nelasot simbolus.
- Spēja pārsūtīt uz jebkuru skaitu stāvokļu konkrētai ievadei.
Tomēr šīs iepriekš minētās funkcijas nepievieno NFA jaudu. Ja salīdzinām abus pēc jaudas, abi ir līdzvērtīgi.
Iepriekš minēto papildu funkciju dēļ NFA ir cita pārejas funkcija, pārējais ir tāds pats kā DFA.
?: Transition Function ?: Q X (? U ? ) -->2 ^ Q.>>Kā redzat, pārejas funkcija ir paredzēta jebkurai ievadei, ieskaitot nulli (vai?), NFA var pāriet uz jebkuru stāvokļu skaitu. Piemēram, zemāk ir NFA iepriekšminētajai problēmai.
2. attēls. NFA stāvokļa pārejas diagramma ar ? = {a, b}
Stāvokļa pārejas tabula augstāk esošajam automātam,
| ?ValstsSimbols? | a | b |
|---|---|---|
| q0 | {q0,q1} | q0 |
| q1 | ? | ? |
Viena svarīga lieta, kas jāņem vērā, ir, NFA, ja kāds ievades virknes ceļš ved uz galīgo stāvokli, tad ievades virkne ir pieņemts . Piemēram, iepriekš minētajā NFA ievades virknei 00 ir vairāki ceļi. Tā kā viens no ceļiem ved uz galīgo stāvokli, iepriekš minētā NFA pieņem 00.
Daži svarīgi punkti:
virknes formātā java
- Pamatojums: