Horizontālās līnijas tiek definētas kā līnijas, kas ir paralēlas horizontam vai zemei, tādēļ nosaukums horizontālā līnija . Horizontālajai līnijai ir nulles slīpums, t.i., šo līniju slīpuma leņķis ir nulle grādi. Ja horizontālās līnijas ir novilktas uz Dekarta plaknēm, tās veido pārtveršanu tikai gar y asi, jo tās vienmēr ir paralēlas x asij un nekad to negriež.
Šajā rakstā mēs detalizēti uzzināsim par horizontālo līniju, tās īpašībām, horizontālās līnijas slīpumu, horizontālās līnijas vienādojumu, piemēriem un BUJ saistībā ar horizontālajām līnijām un citiem.
Satura rādītājs
- Horizontālās līnijas definīcija
- Horizontālās līnijas slīpums
- Horizontālās līnijas zīmēšana
- Horizontālās līnijas vienādojums
- Horizontālās līnijas pārbaude
- Horizontālās un vertikālās līnijas
- Atšķirības starp vertikālajām un horizontālajām līnijām
- Īsa piezīme par horizontālo līniju
- Horizontālo līniju piemēri
Horizontālās līnijas definīcija
Mēs zinām, ka līnija ir taisns ceļš, kas savieno divus vai vairākus divus punktus un stiepjas līdz bezgalībai. Tādējādi mēs definējam horizontālās līnijas kā līnijas, kas ir paralēlas zemei vai horizontam un atrodas nemainīgā augstumā no zemes.
Ja mēs šīs līnijas uzzīmējam Dekarta sistēmā, tad šīs līnijas ir līnijas, kurām nav krustpunkta uz x ass, bet ir krustpunkts uz y ass. Horizontālajām līnijām ir nulles slīpums, t.i., tām ir nulles leņķis ar x asi vai zemi.
Horizontālās līnijas veido pamatu dažādiem objektiem, formām un figūrām, ko mēs pētām ģeometrijā. Pieņemsim, ka mums ir jāzīmē taisnstūris, kvadrāts, trīsstūris, trapece uc, tad šo skaitļu pamatā galvenokārt ir horizontālas līnijas. Horizontālos melus mēs novērojam arī dzīvē, jo līnijas uz telpu grīdas un jumta, kāpņu pamatnes utt. veido arī horizontālās līnijas.
Šīs līnijas sauc arī par gulēšanas līnijām, jo tām nav vertikālas kustības un tās vienmēr atrodas nemainīgā augstumā no zemes. Tālāk pievienotajā attēlā redzama horizontālā līnija.
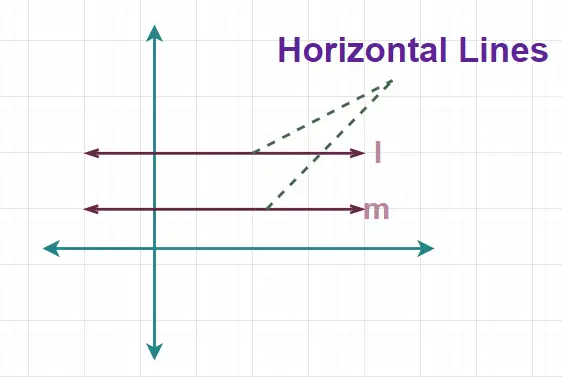
Šeit iepriekš pievienotajā attēlā līnijas l un m ir horizontālas līnijas.
Horizontālās līnijas slīpums
Mēs jau minējām, ka horizontālās līnijas slīpums ir nulle . Tagad uzzināsim, kā horizontālās līnijas slīpums ir nulle. Mēs aprēķinām horizontālās līnijas slīpumu, izmantojot formulu,
Slīpums = Rise/Run
VAI
Līnijas slīpums = izmaiņas y-koordinātā/izmaiņas x-koordinātā
Kur Rise ir augstums, ko līnija iegūst, skrienot no kreisās uz labo pusi, jo mēs jau zinām, ka horizontālā līnija ir paralēla x asij un vienmēr atrodas nemainīgā augstumā, tāpēc mēs sakām, ka šīm līnijām ir nulle pieaugums, tāpēc šo līniju slīpums ir,
Tādējādi Slīpums = 0/Run = 0
Tādējādi tiek secināts, ka horizontālās līnijas slīpums ir nulle.
Horizontālās līnijas zīmēšana
Horizontālās līnijas ir viegli novilkt, izmantojot tālāk aprakstītās darbības,
1. darbība: Paņemiet punktu Dekarta plaknē, kuram jāatrod horizontālā līnija. Pieņemsim, ka punkts ir (1, 2)
java Būla2. darbība: Atzīmē punkta y-koordinātu. Šajā gadījumā y-koordināta ir 2.
3. darbība: Atzīmējiet citus punktus, kur y koordināta ir tāda pati kā 1. darbības punkts. Lai pārējie punkti ir (-2, 2), (0, 2) un (7, 2)
4. darbība: Savienojiet visus punktus, lai iegūtu līnijas segmentu, un pagariniet tos abās pusēs, lai iegūtu horizontālu līniju.
Šī ir vajadzīgā horizontālā līnija, kas iet caur punktu (1, 2), un tās slīpums ir nulle.

Horizontālās līnijas vienādojums
Mēs zinām, ka taisnes vienādojums 2-D koordinātu sistēmā ir,
y = mx + c
kur,
- m ir līnijas slīpums
- c ir krustpunkts uz y ass
Mēs zinām, ka horizontālajai līnijai slīpums ir nulle. Aizstājot šo vērtību iepriekš minētajā vienādojumā, mēs iegūstam horizontālās līnijas vienādojumu,
y = 0x + c
y = c
Kur c ir konstante.
Tādējādi iepriekš minētais vienādojums y = c ir horizontālās līnijas vienādojums.
Šis vienādojums nozīmē, ka horizontālā līnija ir līnija, kas iet cauri visiem Dekarta līnijas punktiem, kur y koordināta ir vienāda ar “c”. Šai līnijas griezumam nav x koordinātu, tāpēc šī līnija nekad negriež x asi, bet y asi punktā (0, c).
Tādējādi mēs varam teikt, ka horizontālās līnijas vienādojums ir, y = c(konstante) un tas iet caur punktu (a, c), kur a var iegūt jebkuru vērtību un c vienmēr ir nemainīgs.
Horizontālās līnijas pārbaude
Tests, ko izmanto, lai noteiktu, vai funkcija ir viena pret vienu funkcija, ir horizontālās līnijas tests. Horizontālās līnijas testā mēs novelkam horizontālu līniju, kas iet caur jebkuru funkcijas punktu, un, ja līnijas nogriež funkciju jebkurā citā punktā, funkcija NAV viena pret vienu funkcija. Tādējādi, lai funkcija būtu viena pret vienu, tai ir jāiztur horizontālās līnijas tests, t.i., jebkurai horizontālajai līnijai funkcija ir jāizgriež tikai vienu reizi.
Mēs zinām, ka funkcijas viens pret vienu ir funkcijas, kurās katrai x vērtībai mums ir tikai viena y vērtība. Tātad, ja horizontālā līnija iet caur funkciju un nogriež to tikai vienu reizi, mēs varam teikt, ka y unikālajai vērtībai mums ir unikāla vērtība x. Bet, ja horizontālā līnija nogriež funkciju vairāk nekā vienu reizi, mēs iegūstam divas vērtības unikālajai y vērtībai, kas nav funkcija viens pret vienu.
Horizontālās līnijas pārbaude palīdz mums noteikt, vai funkcija ir viena funkcija. To var saprast, izmantojot tālāk pievienoto attēlu.

Pirmajā attēlā funkcija ir viens pret vienu, jo horizontālā līnija iet cauri tikai vienam funkcijas punktam.
Otrajā attēlā funkcija NAV viens pret vienu, jo horizontālā līnija iet cauri vairāk nekā vienam funkcijas punktam.
Horizontālās un vertikālās līnijas
Horizontālās līnijas ir līnijas, kas ir paralēlas zemei vai horizontam. Šīs līnijas sauc arī par gulēšanas līnijām. Dekarta sistēmā šīs līnijas ir paralēlas x asij, savukārt vertikālajām līnijām tās ir līnijas, kas ir perpendikulāras horizontālajām līnijām, tās sauc par stāvlīnijām. un ir paralēli y asij Dekarta sistēmā.
Horizontālās līnijas ir līnijas, kas iet no kreisās uz labo pusi Dekarta sistēmā, turpretim vertikālās līnijas ir līnijas, kas iet uz augšu un uz leju Dekarta sistēmā.
Vertikālās un horizontālās līnijas ir perpendikulāras viena otrai. Tālāk pievienotajā attēlā redzama vertikāla un horizontāla līnija.

Atšķirības starp vertikālajām un horizontālajām līnijām
Atšķirības starp vertikālajām un horizontālajām līnijām var viegli saprast, izpētot tālāk pievienoto tabulu.
| Horizontālā līnija | Vertikālā līnija |
|---|---|
| Šīs līnijas ir paralēlas zemei vai horizontam. | Šīs līnijas ir perpendikulāri uz zemi vai horizontu. |
| Horizontālās līnijas slīpums ir nulle. | Vertikālās līnijas slīpums nav noteikts. |
| Horizontālā līnija izveidoja nulles grādu leņķi ar horizontu. | Vertikālā līnija izveidoja 90 grādu leņķi ar horizontu. |
| Vienādojums horizontālajai līnijai, kas iet caur punktu (h, k), ir: y = k | Vertikālās līnijas vienādojums, kas iet caur punktu (h, k), ir: x = h |
| Horizontālās līnijas ir paralēlas x asij Dekarta sistēmā. | Vertikālās līnijas ir paralēlas y asij Dekarta sistēmā. |
| Piemēri, kas attēlo horizontālās līnijas, ir:
| Vertikālo līniju piemēri ir:
|
Īsa piezīme par horizontālo līniju
Horizontāla līnija matemātikā ir pilnīgi līdzena, paralēla horizontam. Tas iet no kreisās puses uz labo, un tā slīpums ir 0. Ģeometrijā tā tiek attēlota kā taisna līnija, kas savieno jebkurus divus punktus vienā augstumā plaknē. Horizontālās līnijas vienādojums ir formā (y = k), kur (k) ir nemainīga vērtība, kas apzīmē līnijas augstumu uz y ass.
Lasīt vairāk:
- Līniju veidi
- Paralēlas līnijas
- Kā pievienot horizontālu līniju HTML?
- Kā HTML izmantot pilnīgu horizontālo līniju atstarpi?
- Kā zīmēt horizontālas un vertikālas līnijas Android lietotnē, izmantojot XML
Horizontālo līniju piemēri
1. piemērs: atrodiet vienādojumu horizontālajai līnijai, kas iet caur punktu (1, -1).
Risinājums:
Mēs zinām, ka horizontālās līnijas slīpums ir m = 0.
Dotais punkts (1, -1)
Taisnes vienādojums, kas iet caur punktu (x1, un1) un slīpums (m) ir,
un – un1= m(x – x1)
Aizstājot vērtības iepriekš minētajā vienādojumā, mēs iegūstam,
y — (-1) = 0 (x – 1)
un + 1 = 0
y = -1
Tādējādi horizontālās līnijas vienādojums, kas iet caur punktu (1, -1), ir, y = -1
2. piemērs: atrodiet vienādojumu horizontālajai līnijai, kas iet caur punktu (5, 9).
Risinājums:
Mēs zinām, ka horizontālās līnijas slīpums ir m = 0.
Dotais punkts (5., 9.)
Taisnes vienādojums, kas iet caur punktu (x1, un1) un slīpums (m) ir,
un – un1= m(x – x1)
Aizstājot vērtības iepriekš minētajā vienādojumā, mēs iegūstam,
y — (9) = 0 (x – 5)
un – 9 = 0
y = 9
Tādējādi horizontālās līnijas vienādojums, kas iet caur punktu (5, 9), ir: y = 9
3. piemērs. Atrodiet horizontālās līnijas vienādojumu, ja līnijas y krustpunkts ir 5.
Risinājums:
Horizontālās līnijas vienādojums ir,
y = k
kur k ir y-pārtvērums
Ņemot vērā
- k = 5
Horizontālās līnijas vienādojums,
y = 5
Tādējādi vienādojuma horizontālā līnija ar y krustpunktu ir 5, y = 5
4. piemērs. Atrodiet horizontālās līnijas vienādojumu, kad līnijas y krustpunkts ir -11/3.
Risinājums:
Horizontālās līnijas vienādojums ir,
y = k
kur k ir y-pārtvērums
Ņemot vērā
- k = -11/3
Horizontālās līnijas vienādojums,
y = -11/3
3 g = -11
3 g + 11 = 0
Tādējādi vienādojums horizontālā līnija ar y krustpunktu kā -11/3 ir 3y + 11 = 0
Horizontālās līnijas — FAQ
Kas ir horizontālās līnijas?
Horizontālās līnijas ir līnijas, kas ir paralēlas horizontam vai zemei. Dekarta sistēmā horizontālās līnijas ir paralēlas x asij.
Kas ir horizontālās līnijas vienādojums?
Horizontālās līnijas vienādojums ir,
y = k
kur k ir krustpunkts uz y ass.
Kāds ir horizontālās līnijas slīpums?
Horizontālās līnijas slīpums vienmēr ir vienāds ar nulli, jo tās veido nulles grādu leņķi ar x asi.
Kādi ir horizontālo līniju piemēri?
Piemēri, kas attēlo horizontālās līnijas, ir:
manuāla pārbaude
- Taisns ceļš
- Kāpņu apakšdaļa
- Jebkuras figūras pamatne utt.
Kā sauc horizontālās līnijas uz zemeslodes?
Horizontālās līnijas, kas iet uz zemeslodes, sauc par platuma grādiem, un tās iet paralēli ekvatoram.
Kādas ir horizontālo līniju īpašības?
Horizontālo līniju dažādas īpašības ir,
- Tie ir paralēli zemei, horizontam un x asij.
- Tie ir perpendikulāri y asij.
- Horizontālās līnijas slīpums ir nulle utt.
Kura līnija ir vertikāla un horizontāla?
Vertikāla līnija ir paralēla y asij un virzās taisni uz augšu un uz leju koordinātu plaknē, savukārt horizontāla līnija ir paralēla x asij un iet taisni pa kreisi un pa labi.
Kāds ir horizontālās un vertikālās līnijas slīpums?
Līnijas slīpums norāda tās stāvumu un virzienu. To aprēķina kā vertikālo izmaiņu attiecību pret horizontālajām izmaiņām starp diviem līnijas punktiem.
Kādas ir horizontālās un vertikālās punktu līnijas?
Horizontālās līnijas stiepjas no kreisās puses uz labo vai no labās uz kreiso un iet paralēli x asij, savukārt vertikālās līnijas stiepjas uz augšu un uz leju un iet paralēli y asij. Šie divu veidu līnijas ir perpendikulāras viena otrai.
