uz Kosinusa funkcija vai cos Īsāk sakot, funkcija ir viena no sešām Trigonometriskās funkcijas trigonometrijas pamats. Trigonometrijā kosinuss ir dots kā taisnleņķa trīsstūra pamatnes attiecība pret hipotenūzu. Kosinusa funkcija tiek attēlota kā Cos x, kur x ir leņķis, kuram tiek aprēķināta kosinusa attiecība. Runājot par funkciju, mēs varam teikt, ka x ir kosinusa funkcijas ievade vai domēns.

To plaši izmanto daudzos mācību priekšmetos, piemēram, fizikā, ģeometrijā un inženierzinātnēs, cita starpā, galvenokārt izmantojot tā periodisko raksturu. Piemēram, to izmanto, lai definētu skaņas viļņu viļņu raksturu, elektriskās plūsmas aprēķinus caur plakanu virsmu utt. Šajā rakstā mēs detalizēti uzzinām, kas ir kosinusa funkcija, domēns un diapazons kosinusa funkcijas, perioda un kosinusa funkcijas grafika.

Satura rādītājs

• Kas ir kosinusa funkcija?
• Cos vienības aplī
• Kosinusa funkciju grafiks
• Apgrieztā kosinusa funkcija
• Kosinusa funkcija aprēķinos
• Cos funkciju identitātes

Kas ir kosinusa funkcija?

Kosinusa funkcija ir trigonometriska funkcija, kas būtībā ir periodiska. Kosinusa funkciju izsaka kā cos x, kur x ir viens no taisnleņķa trīsstūra asajiem leņķiem. Kosinusa funkcija atrod bāzes un hipotenūzas attiecību noteiktai x vērtībai. Kosinusa funkcija ir saīsināta kā cos(x) vai cos(θ), kur x ir leņķis radiānos un teta θ ir leņķis grādiem vispār. Kosinusa funkciju var definēt, izmantojot vienības apli, t.i., apli ar vienības rādiusu, kā mēs redzēsim vēlāk šajā rakstā. Tas ir periodisks un atkārto savas vērtības pēc katras pilnīgas leņķu pagriešanas. Dekarta plaknē to var saukt par hipotenūzas vektora komponentu paralēli x asij.

Kosinusa funkcijas definīcija

Kosinusa funkcija ir definēta taisnleņķa trīsstūrī kā attiecīgā leņķa blakus esošās malas garuma attiecība pret hipotenūzas garumu. Matemātiski kosinusa funkcija ir dota kā

Cos x = Cos θ = pamatnes garums/hipotenūzas garums = b/h = OB/OA

kur x ir leņķis radiānos un θ ir ekvivalentais leņķis grādos.

Cos funkciju domēns un diapazons

Mēs zinām, ka funkcijai domēns ir pieļaujamās ievades vērtības un diapazons ir izvades vērtība konkrētajai ievades vai domēna vērtībai. Tādējādi mēs varam pieņemt, ka funkcija darbojas kā procesors, kas ņem ievadi, apstrādā to un dod noteiktu izvadi. Cos funkcijas domēns un diapazons ir apskatīts tālāk:

• Kosinusa funkcijas domēns: R i., visu reālo skaitļu kopa.
• Kosinusa funkcijas diapazons: [-1, 1], t.i., izvade mainās starp visiem reālajiem skaitļiem no -1 līdz 1.

Kosinusa funkcijas periods

The funkciju pēc būtības ir periodisks, t.i., atkārtojas pēc 2π vai 360°. Citiem vārdiem sakot, tas atkārtojas pēc katras pilnīgas rotācijas. Tādējādi kosinusa funkcijas periods ir pilnīga rotācija vai 360° leņķis (vai 2π).

Kosinusa funkcijas apgrieztā vērtība

Kosinusa funkcijas apgrieztā vērtība ir pazīstama kā sekants funkcija vai sek īsumā. Matemātiski kosinusa funkcijas apgrieztā vērtība ir dota kā

java Būla

sek(θ) = 1/cos(θ)

Saskaņā ar noteikumiem Savstarpēji , ja mēs reizinām Cos x ar Sec x, reizinājums vienmēr būs 1.

Kosinusa funkciju grafiks

Kosinusa funkcijas grafiks atgādina sinusa funkcijas grafiku ar būtisku atšķirību, ka pie x = 0 sin funkcijas grafiks iet no sākuma, bet pie x = 0, kosinusa funkcijas grafiks iet no (0, 1) pie y-aix. Tālāk ir parādīts kosinusa funkcijas vērtības grafiks, t.i., y = cos x

Iepriekš apskatītās īpašības var redzēt grafikā, piemēram, funkcijas periodiskumu.

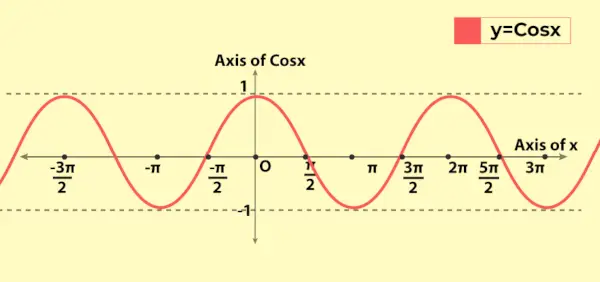
Kosinusa funkcijas variācijas grafikā

Tā kā kosinusa funkcijas diapazons ir [-1, 1], tāpēc tas grafikā mainās no -1 līdz 1. Tam ir periodisks raksturs, jo grafiks atkārtojas pēc katra garuma 2π uz x ass. Tas atspoguļo, ka kosinusa funkcijas periods ir 2π (vai 360°).

Cos vienības aplī

Kosinusa funkciju var definēt, izmantojot vienības apli. Sapratīsim, kā mēs varam definēt kosinusa funkciju vienības apļa izteiksmē.

Apsveriet līnijas segmentu OA, kas rotē ap punktu O, kur O ir taisnleņķa plaknes sākums. Tādējādi OA rotācija apraksta vienības apli (vienības rādiusa apli), kura centrs ir sākuma punktā O un punkts A vienmēr atrodas uz šī apļa. Ja nometam perpendikulu no A uz x ass un krustpunktu saucam par B, un θ ir leņķis, ko OA veido ar pozitīvo x ass virzienu, tad cos(θ) = hipotenūzas projekcija uz x -ass = OB/|OA| = OB (jo |OA| = 1 vienība).

Ņemiet vērā, ka virziens OB ir svarīgs, kā redzams turpmākajos attēlos. Zaļais segments apzīmē cos(θ) garumu/lielumu, un bultiņa apzīmē virzienu (+ve vai -ve)

Ņemiet vērā, ka cos (θ) vērtība ir pozitīva θ, kas pieder pirmajam un ceturtajam kvadrantam, bet negatīva θ, kas pieder otrajam un trešajam kvadrantam.

Apgrieztā kosinusa funkcija

Apgrieztā kosinusa funkcija, kas pazīstama kā loka-kosinuss funkcija un saīsināti kā arccos(x) vai cos ^-1 (x) ir definēts šādi

cos(x) = y

⇒ cos ^-1 (y) = x

Apgrieztās kosinusa funkcijas domēns un diapazons

Apgrieztās kosinusa funkcijas domēns un diapazons ir minēti zemāk:

• Apgrieztās kosinusa funkcijas domēns: Visi reālie skaitļi diapazonā [-1, 1]
• Apgrieztās kosinusa funkcijas diapazons: Visi reālie skaitļi diapazonā [0, π]

Hiperboliskā kosinusa funkcija

Hiperboliskās funkcijas ir analogas trigonometriskās funkcijas ekvivalents, kuru algebriskā izteiksme ir eksponenciālās funkcijas izteiksmē. Hiperboliskā kosinusa funkcija, kas saīsināta kā cosh (x) kur x ir hiperboliskais leņķis ir hiperboliskās ģeometrijas jēdziens. Tāpat kā (cos(x), sin(x)) apzīmē punktu uz vienības apļa, (cosh(x), sinh(x)) apzīmē punktu uz vienības hiperbolas, t.i., xy = 1, kur sinh(x) ir hiperbolisks sinusa funkcija. Hiperboliskās cos funkcijas algebriskais izvērsums ir dots kā

cosh(x) = (e ^x + un ^-x )/2

Sīkāka informācija par hiperboliskajām funkcijām ir ārpus šī raksta darbības jomas, taču varat to atsaukties Šis raksts .

Kosinusa funkcija aprēķinos

Aprēķinu nozare matemātikā nodarbojas ar diferenciācija un integrācija noteiktas funkcijas. Funkcijas diferencēšana ir funkcijas izmaiņu ātrums attiecībā pret neatkarīgo mainīgo, savukārt integrācija ir apgriezts diferenciācijas process, kas nodarbojas ar funkcijas integrāļa atrašanu, kuras atvasinājums pastāv.

Kosinusa funkcijas atvasinājums

The atvasinājums kosinusa funkcija ir vienāda ar sinusa funkcijas negatīvo. Matemātiski

d(cos(x))/dx = -sin(x)

Kosinusa funkcijas integrācija

The nenoteikts integrālis kosinusa funkcija ir vienāda ar sinusa funkciju. matemātiski -

∫cos(x)dx = sin(x) + C, kur C ir integrācijas konstante.

Sinusa un kosinusa funkcijas

Šajā grafikā ir parādīta galvenā atšķirība starp sinusa un kosinusa funkciju:

Atšķirība starp sinusa un kosinusa funkcijām

Nākamajā tabulā ir norādītas atšķirības starp sinusa un kosinusa funkciju -

Cos vērtību tabula

Nākamajā tabulā ir sniegtas kosinusa funkcijas vērtības dažiem kopīgiem leņķiem Dekarta plaknes pirmajā kvadrantā -

Mēs varam viegli aprēķināt citu izplatītu leņķu, piemēram, 15°, 75°, 195°, -15° utt. vērtības, izmantojot šīs vērtības, izmantojot formulas cos (x + y) un cos (x - y), kas aprakstītas vēlāk šajā sadaļā. rakstu.

Pārbaudiet, Trigonometriskā tabula

Cos funkciju identitātes

Galvenās trigonometriskās identitātes, kas saistītas ar kosinusa funkciju, ir minētas zemāk:

• bez²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/s(x)
• cos 2x = cos²x – grēks²x = 1 – 2sin²x = 2cos²x – 1 = (1 – iedegums²x/1 + iedegums²x)
• cos 3x = 4cos³x – 3cos x

Saistītie raksti

• Trigonometrisko funkciju diferenciācija
• Apgrieztās trigonometriskās funkcijas
• Apgrieztie trigu atvasinājumi

Atrisināti kosinusa funkcijas piemēri

Šeit ir daži atrisināti piemēri, kas palīdzēs labāk izprast kosinusa funkcijas jēdzienu.

1. piemērs. Kādas ir kosinusa funkcijas maksimālās un minimālās vērtības?

Risinājums:

Maksimālā kosinusa funkcijas vērtība ir 1 pie 0° un 180°, savukārt funkcijas minimālā vērtība ir -1 pie 180°.

2. piemērs. Kādā leņķī(-os) diapazonā [0, 360] ir kosinusa funkcijas vērtība 0?

Risinājums:

Kosinusa funkcijas vērtība ir 0 leņķos 90° un 270°.

3. piemērs. Kādiem kvadrantiem kosinusa funkcijas vērtība ir negatīva?

Risinājums:

Kosinusa funkcija ir negatīva II^ndun III^rdkvadranti.

4. piemērs: aprēķiniet cos vērtību (45°).

Risinājums:

kas ir skaļrunis

Saskaņā ar iepriekš sniegto 4. identitāti cos(-x) = cos(x).

Tāpēc cos(-45°) = cos(45°) = 1/√2

5. piemērs. Aprēķiniet cos(15°) vērtību.

Risinājums:

Izmantojot iepriekš norādīto 3. identitāti –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

6. piemērs. Kas ir cos ^-1 (1/2) diapazonā [0,π]?

Risinājums:

Ļaujiet cos^-1(1/2) = y.

Tāpēc cos(y) = 1/2 ⇒ y = π/3 iepriekš dotajā diapazonā.

Tādējādi atbilde ir π/3.

7. piemērs. Kāda ir cos(-15°) vērtība?

Risinājums:

Izmantojot iepriekš norādīto 3 identitāti –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Alternatīvi, mēs varam arī izmantot identitāti cos(-x) = cos(x) un izmantot cos(15°) vērtību, kas aprēķināta 5. piemērā.

8. piemērs. Aprēķiniet laukumu zem kosinusa funkcijas grafika no x = 0 līdz x = π/2.

Risinājums:

Doto laukumu var aprēķināt, atrisinot šādu noteiktu integrāli –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Tāpēc atbilde ir 1 kvadrāta vienība.

9. piemērs. Ja cos(x) = π/3, atrodiet cos(3x) vērtību (decimāldaļā ar divu ciparu precizitāti aiz komata).

Risinājums:

Izmantojot identitāti – cos(3x) = 4cos³(x) – 3cos (x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

10. piemērs. Atrodiet cos(120°) vērtību.

Risinājums:

Cos (2x) identitātes izmantošana

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1-2⨉ (√3/2)²= 1 – 3/2 = -1/2

Prakses jautājumi: Cos funkcijas

Q1. Kāda ir formula, lai aprēķinātu leņķa cos taisnleņķa trijstūrī?

Q2. Kāda ir cos ģeometriskā interpretācija Dekarta plaknē?

Q3. Aprēķiniet cos(120°) vērtību.

Q4. Atrodiet cos vērtību ^-1 (√3/2) diapazonā [π, 2π].

Q5. Ja stabs met uz zemes tāda paša garuma ēnu, atrodiet saules leņķi attiecībā pret zemi, ja saule ir austrumu virzienā.

Kopsavilkums – kosinusa funkcija

Kosinusa funkcija, kas apzīmēta kā cos(x), ir pamata trigonometriskā funkcija, kas definēta kā pamatnes attiecība pret hipotenūzu taisnleņķa trijstūrī, un tās periodiskuma dēļ tā ir būtiska dažādās jomās, piemēram, fizikā, inženierzinātnēs un ģeometrijā. , kas ir noderīga viļņu uzvedības modelēšanā. Tam ir visu reālo skaitļu domēns un diapazons no -1 līdz 1, atkārtojot savu ciklu ik pēc 2 Pi radiānos vai 360 grādos, kas redzams no tā viļņveidīgā grafika, kas sākas ar (0,1). Aprēķinu ziņā cos(x) atvasinājums ir − sin( x ), un tā integrālis rada sin( x )+ C , ar C kā integrācijas konstanti. Šī funkcija attiecas arī uz hiperboliskām formām, piemēram, cosh (x), uzlabojot tās pielietojumu dažādos matemātiskajos kontekstos un risinājumos, tostarp viļņu aprēķinos un svārstības fiziskajās sistēmās.

Kosinusa funkcija: FAQ

1. Kas ir kosinusa funkcija?

Kosinusa funkcija ir viena no galvenajām trigonometriskajām funkcijām. Tas ir definēts taisnleņķa trijstūrī kā attiecīgajam leņķim blakus esošās malas garuma attiecība pret hipotenūzas garumu.

2. Vai trigonometrijā cos un kosinuss ir vienādi?

Jā. cos ir kosinusa funkcijas saīsinājums/īsa forma.

3. Kāds ir Cos funkcijas diapazons?

Cos vai kosinusa funkcijas diapazons ir visi reālie skaitļi no -1 līdz 1, t.i., [-1,1].

4. Kas ir Cos funkcijas domēns?

Cos vai kosinusa funkcijas domēns ir visu reālo skaitļu ser, t.i., R .

5. Kāda ir kosinusa funkcijas maksimālā vērtība?

Maksimālā kosinusa funkcijas vērtība ir 1 visiem leņķiem, kas līdzvērtīgi 0° vai 360°.

6. Kāda ir kosinusa funkcijas minimālā vērtība?

Kosinusa funkcijas minimālā vērtība ir -1 visiem leņķiem, kas līdzvērtīgi 180°.

7. Kā atrast Cos(-x) vērtību?

Cos(-x) vērtību var aprēķināt, aprēķinot cos(x) vērtību, jo pastāv šāda identitāte: cos(-x) = cos(x).

8. Kā izveidot kosinusa funkcijas grafiku?

Lai uzzīmētu kosinusa funkcijas grafiku dekarta plaknē, skatiet x asi kā leņķus radiānos (vai grādos) un y asi kā kosinusa funkcijas vērtības atbilstošajam leņķim uz x ass. Tagad

• 1. darbība: Paņemiet x ass apakškopu, kurai vēlaties uzzīmēt grafiku.
• 2. darbība: Sadaliet x asi šajā diapazonā vienādos attālumos (t.i., starp visiem apakšpunktiem ir vienāda atstarpe). Ņemiet vērā, jo lielāks ir dalījumu skaits, jo lielāka ir iegūtā grafika precizitāte.
• 3. darbība: Katram no šiem apakšpunktiem x atzīmējiet grafikā punktu (x, cos(x)).
• 4. darbība: Savienojiet visus atzīmētos punktus, lai iegūtu kosinusa funkcijas grafiku (jūsu atlasītajai x ass apakškopai).

9. Kā atrast kosinusa funkcijas periodu?

Kosinusa funkcijas periods attiecas uz minimālo vērtību diapazonu, pēc kura funkcija sāk sevi atkārtot. Mēs zinām, ka kosinusa funkcija atkārtojas pēc katras pilnīgas rotācijas, kas nozīmē 2π radiānus. Tāpēc kosinusa funkcijas periods ir 2π radiāni jeb 360°.

10. Kas ir kosinusa funkcijas amplitūda?

Kosinusa funkcijas amplitūda attiecas uz funkcijas maksimālās vērtības nobīdi no vidējās pozīcijas, t.i., x ass. Kosinusa funkcijas amplitūda ir 1, jo maksimālā nobīde ir 1 (vērtībām -1 un 1 attiecīgi pie 180 un 0 grādiem. Ņemiet vērā, ka kosinusa funkcijas diapazons ir [-amplitūda, amplitūda].