A Funkcija matemātikā ir īpaša saistība starp ievades vērtību kopu un izvades vērtību kopu. Funkcijā katra ievades vērtība dod noteiktu izvades vērtību. Mēs attēlojam funkciju matemātikā kā, y = f(x) kur x ir ievades vērtība un katram x mēs iegūstam izejas vērtību kā y.

Šajā rakstā mēs uzzināsim par funkcijas matemātikā, to dažādie veidi, piemēri un citas sīkāk.

Satura rādītājs

• Kas ir funkcija matemātikā?
• Funkciju definīcija matemātikā
• Funkciju piemēri
• Nosacījums funkcijas veikšanai
• Funkciju attēlojums matemātikā
• Funkcijas identifikācija
• Funkciju veidi
• Kas ir funkcija algebrā?
• Domēns un funkciju diapazons
• Funkciju sastāvs
• Funkciju algebra
• Kas ir funkcija grafikā?
• Grafiku funkcijas
• Kopējās funkcijas
• Funkciju lietojumprogrammas
• Funkcijas piemēri
• Praktizējiet problēmas par to, kas ir funkcija

Kas ir funkcija matemātikā?

Funkcija matemātikā ir a attiecības starp doto kopu ievades vērtībām (domēns) un izejas vērtībām (diapazons) tā, lai divi mainīgie no domēnu kopām nebūtu saistīti ar vienu un to pašu mainīgo diapazonu kopā. Vienkāršs funkcijas piemērs matemātikā ir f(x) = 2x, kas ir definēts R→R, šeit jebkurš domēna mainīgais ir saistīts tikai ar vienu mainīgo diapazonā.

Matemātikas funkcijai ir domēns, kodomēns un diapazons. Domēns ir visu iespējamo x vērtību kopa, un funkcijas diapazons ir visu y izvades vērtību kopa. Diapazons ir funkcijas kodomēna apakškopa. Mēs varam arī teikt, ka funkcija matemātikā ir relācija ar unikālu izvadi, un nevienai divām ievades vērtībām nav līdzīgas izejas funkcijā, kā tas ir relācijas gadījumā.

Funkciju definīcija matemātikā

Funkcija ir īpaša sakarība vai metode, kas savieno katru kopas A locekli ar unikālu kopas B locekli, izmantojot noteiktu relāciju. Kopu A sauc par domēnu, un kopu B sauc par funkcijas kopdomēnu. Funkcija matemātikā no kopas A līdz kopai B tiek definēta šādi:

f = ∀ a ∈ A, b ∈ B

pasta pasūtījumu šķērsošana

Katra funkcija ir relācija, bet katra relācija nav funkcija. Kritēriji jebkuras attiecības uzskatīšanai par funkciju, jo funkcijā katram kopas A elementam kopā B ir tikai viens attēls, savukārt kopas A elementam kopā B var būt vairāk nekā viens attēls.

Mēs definējam funkcijas matemātikā no netukšas kopas A līdz netukšai kopai B tā, ka

(a, b) ∈ f, tad f(a) = b

kur mēs zvanījām b kā attēls a definēts zem attiecības f .

Katrs elements 'a' komplektam A ir unikāls attēls ' b ' kopā B, tad tā ir funkcija.

Funkciju piemēri

Funkcija matemātikā f ir definēta kā, y = f(x) kur x ir ievades vērtība, un katrai x ievades vērtībai mēs iegūstam unikālu y vērtību. Dažādi R→R definēto funkciju piemēri matemātikā ir:

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3 utt

Nosacījums funkcijas veikšanai

Jebkurām divām kopām A un B, kas nav tukšas, funkcija f: A→B apzīmē to f ir funkcija no A līdz B, kur A ir domēns un B ir kopdomēns.

Jebkuram elementam a ∈ A, unikāls elements, b ∈ B ir tāds, ka (a, b) ∈ f. Unikālais elements b, kas ir saistīts ar a, tiek apzīmēts ar f(a) un tiek lasīts kā f no a. To var labāk saprast no tālāk redzamā attēla:

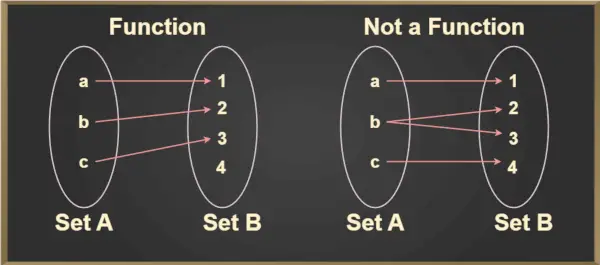
Vertikālās līnijas pārbaude

Vertikālās līnijas testu izmanto, lai noteiktu, vai līkne ir funkcija vai nē. Ja kāda līkne nogriež vertikālu līniju vairāk nekā vienā punktā, tad līkne nav funkcija.

Funkciju attēlojums matemātikā

Mēs attēlojam funkciju matemātikā kā,

y = f(x) = x + 3

Šeit x vērtību kopa ir funkcijas domēns, un y izvades vērtību kopa ir funkcijas līdzdomēns. Šeit funkcija ir definēta visiem reālajiem skaitļiem, jo ​​tā dod unikālu vērtību katram x, bet ne vienmēr ir iespējams iegūt izvadi katrai x vērtībai, tādā gadījumā funkciju definējam divās daļās, to var saprast kā

• f(x) = 1/(x – 2), kur x ≠ 2
• f(x) = x²kur x ∈ {R}

Mēs varam definēt funkciju matemātikā kā mašīnu, kas ņem zināmu ievadi un dod unikālu rezultātu. Funkcija f(x) = x²tālāk ir definēts kā

Mēs varam attēlot funkciju matemātikā ar trim metodēm kā:

• Pasūtīto pāru komplekts
• Tabulas forma
• Grafiskā forma

Piemēram, ja mēs attēlojam funkciju kā, f (x) = x³

Vēl viens veids, kā attēlot to pašu funkciju, ir kā pasūtīto pāru komplekts kā,

f = {(1,1), (2,8), (3,27)}

Iepriekš minētajā kopā funkcijas domēns ir D = {1, 2, 3} un funkcijas diapazons ir R = {1, 8, 27}

Funkcijas identifikācija

Funkcija matemātikā tiek klasificēta kā īpašs attiecību veids. Funkcijas identificēšanai var izmantot šādus noteikumus:

• Relācija, kurā katra ievade ir saistīta ar unikālu izvadi, ir funkcija. Tas izsauca funkciju viens pret vienu.
• Funkcija ir arī relācija, kurā divas ievades (priekšattēli) ir kartētas ar vienu izvadi. Šī funkcija ir daudz pret vienu.
• Relācija, kurā viena ieeja ir kartēta ar divām dažādām izvadēm, nav funkcija.
• Relācija, kurā daudzas ievades tiek kartētas ar daudzām izejām, neievērojot īpašus noteikumus, nav funkcija.

Funkciju veidi

Savādāk Funkciju veidi tiek izmantoti dažāda veida matemātisko problēmu risināšanai, īpaši saistībā ar līknēm un vienādojumiem. Matemātikā ir trīs galvenās funkcijas, kuru pamatā ir elementu kartēšana no kopas A uz kopu B.

Injekcijas funkcija vai viena pret vienu funkcija

Funkciju, kurā katram domēna elementam koddomēnā ir atsevišķs attēls, sauc par Injicējams vai Viens pret vienu funkcija .

f: tiek uzskatīts, ka A → B ir viens pret vienu vai injicējams, ja atšķirīgo A elementu attēli zem f ir atšķirīgi, t.i.,

f(a ₁ ) = b ₁ , f(a ₂ ) = b ₂

kur₁, a₂∈ A un b₁, b₂∈ B

Surjektīvās funkcijas vai Onto funkcija

Surjektīvā funkcija ir funkcija, kurā katram kodomēna elementam domēnā ir priekšattēls. To sauc arī Uz funkciju kas nozīmē, ka katrs kodēna elements ir saistīts ar katru domēna elementu. Nevienam kodēna elementam nedrīkst būt tukša relācija. Kodomēna un diapazona elementu skaits ir vienāds.

f: Tiek uzskatīts, ka A → B atrodas uz, ja katrs B elements ir kāda A elementa attēls zem f, t.i., katram b ϵ B, A eksistē elements 'a' tā, ka f(a) = b.

Bijektīva funkcija

Ja funkcijai ir gan Injekcijas (viens pret vienu), gan Surjektīvas (funkcija Onto) īpašības, tad funkciju sauc par Bijektīva funkcija . Bijektīvajā funkcijā katrs domēna elements ir saistīts ar katru kodomēna elementu, kā arī pastāv attiecības viens pret vienu. Tas nozīmē, ka kodomēna un diapazona elementu skaits ir vienāds un nevienam elementam domēnā vai kodēnā nav tukšas attiecības.

Pamatojoties uz izvades vērtībām, funkcijas tiek klasificētas kā nepāra un pāra funkcijas. Apskatīsim tos

Nepāra funkcijas

Nepāra funkcija ir funkcijas veids, kam ir simetrija attiecībā uz izcelsmi. Konkrēti, ja f(x) ir nepāra funkcija, tā parāda, ka f(-x) = -f(x)

Vienmērīga funkcija

Vienmērīga funkcija ir funkciju veids, kam ir simetrija pret y asi. Konkrēti, ja f(x) ir pāra funkcija, tā parāda, ka f(-x) = f(x)

sadalīt ar virkni java

Kas ir funkcija algebrā?

Funkcija iekšā algebra ir vienādojums, kuram jebkurš x, ko var ievietot vienādojumā, no vienādojuma radīs tieši vienu izvadi, piemēram, y. To attēlo kā y = f(x), kur x ir neatkarīgs mainīgais un y ir atkarīgs mainīgais.

Piemēram:

• y = 2x + 1
• y = 3x – 2
• y = 4 g
• y = 5/x

Domēns un funkciju diapazons

Domēns un diapazons funkcijas ir attiecīgi funkcijas ievades un izvades vērtība. Piemēram, pieņemsim, ka mums ir funkcija, kas dota kā f (x) = x². Šeit mēs varam ņemt visu reālo skaitli kā x ievades vērtību, un izvade vienmēr būs pozitīvs reālais skaitlis. Tādējādi tā domēnā ir visi reālie skaitļi, kas attēloti kā R, savukārt tā diapazons ir pozitīvu reālo skaitļu kopums, kas attēlots kā R⁺

Funkciju sastāvs

Ja f: A → B un g: B→ C ir divas funkcijas. Tad f un g sastāvu apzīmē kā f(g) un definē kā funkciju migla = f(g(x)) x ∈ A.

Ņemsim divas funkcijas f(x) = x + 3 un g(x) = 2x²

migla = f(g(x))

⇒ migla = f(2x²)

⇒ zobs = 2x²+ 3

Uzzināt vairāk, Funkcijas sastāvs

Funkciju algebra

Funkciju algebra ietver algebriskās darbības, kas tiek veiktas starp divām funkcijām. Tālāk ir minēta algebriskā darbība divām funkcijām f(x) un g(x), kas definētas uz x reālās vērtības:

• (f + g) (x) = f (x) + g (x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Jā, k ir reāls skaitlis}
• (f/g)(x) = f(x)/g(x); {G(x) ≠ 0}

Kas ir funkcija grafikā?

Funkciju var viegli attēlot grafikā. Jebkura funkcija grafikā attēlo līkni (ieskaitot taisnu līniju) x-y plaknē, kas kartēta tās ievades un atbilstošajām izvades vērtībām.

Lai attēlotu funkciju, vispirms atrodiet dažus punktus, kas atrodas uz funkcijas, un pēc tam savienojiet šos punktus atbilstoši funkcijas atrašanās vietai. Piemēram, lai attēlotu funkciju (taisnu līniju) f(x) = y = 5x – 2, mums ir nepieciešams kāds punkts grafikā. Lai atrastu punktu grafikā, vispirms ņemam nejaušās x vērtības un pēc tam atrodam tām atbilstošās y vērtības, kā

f(x) = y = 5x-2

ja x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

ja x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

ja x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

Tagad, savienojot šos punktus, mēs varam iegūt funkcijas y = 5x – 2 grafiku

Grafiku funkcijas

Zinot x vērtības, funkciju f(x) var attēlot grafikā. Tā kā y = f(x), mēs varam atrast y saistīto vērtību, sākot ar x vērtībām. Rezultātā mēs varam attēlot grafiku koordinātu plaknē, izmantojot x un y vērtības. Apsveriet šādu scenāriju:

Pieņemsim, ka y = x + 3

Ja x = 0, y = 3

Līdzīgi,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Rezultātā mēs varam attēlot funkcijas x + 3 grafiku, izmantojot šīs vērtības.

Kopējās funkcijas

Dažas kopīgās funkcijas, kuras parasti izmanto matemātikā, ir apskatītas zemāk:

Reāla funkcija

Reāla funkcija matemātikā attiecas uz funkciju, kuras domēns un diapazons ir reālo skaitļu apakškopas (apzīmētas kā ℝ). Vienkāršāk sakot, reālā funkcija ir matemātisks noteikums vai sakarība, kas katrai reālā skaitļa ievadei piešķir reālā skaitļa vērtību.

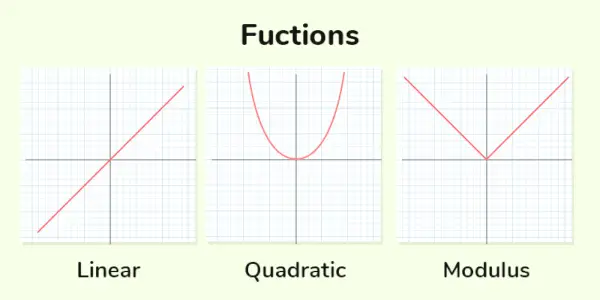
Reālas funkcijas

kurš ir urfi javed

Polinoma funkcija

Funkciju, kurā algebrisko mainīgo eksponenti ir nenegatīvi veseli skaitļi, sauc par Polinoma funkcija . Ja mainīgā jauda ir 1, to sauc par lineāro funkciju, ja jauda ir 2, to sauc par kvadrātfunkciju, un, ja jauda ir 3, to sauc par kubisko funkciju. Tālāk ir minēti daži polinomu funkciju piemēri:

• y = x²
• y = 2x + 3
• y = 3x³

Polinoma funkcijas var iedalīt šādos veidos:

Lineāra funkcija : Lineārā funkcija ir funkcija, kurā mainīgā maksimālā jauda ir 1. Vispārīgā forma Lineāra funkcija ir y = mx + c

Kvadrātiskā funkcija : Kvadrātiskās funkcijas ir tās, kurās mainīgā maksimālā jauda ir 2. Vispārējā forma kvadrātiskā funkcija ir, cirvis ² + bx + c = 0

Kubiskā funkcija : Kubiskā funkcija ir tie, kuros mainīgā maksimālā jauda ir 3. Vispārīga kubiskās funkcijas forma ir dota kā cirvis ³ + bx ² + cx + d = 0

Apgrieztā funkcija

Apgrieztā funkcija ir funkcija, kas satur citas funkcijas apgriezto vērtību. Pieņemsim, ka mums ir funkcija y = f(x), tad tās apgrieztā funkcija būs x = f^-1(y). Ja y = f (x), domēns ir x un diapazons ir y, bet gadījumā, ja x = f^-1(y), domēns ir y un diapazons ir x. Tādējādi mēs varam teikt, ka sākotnējās funkcijas domēns ir tās apgrieztās funkcijas diapazons, bet sākotnējās funkcijas diapazons ir sākotnējās funkcijas domēns. Daži apgriezto funkciju piemēri ir,

• y = tā^-1(x)
• y = x^-1

Apgabala funkcija

Laukuma funkcija parasti attiecas uz matemātisko funkciju, kas aprēķina ģeometriskas formas vai apgabala laukumu. Apgabala funkcija kā ievadi izmanto vienu vai vairākus parametrus un atgriež atbilstošās formas laukumu. Dažas no apgabala funkcijām ir apskatītas tālāk:

Apļa funkcijas zona : Apļa laukums (A) ir tā rādiusa (r) funkcija, lai

A = πr ²

Trīsstūra funkcijas apgabals : Trīsstūra laukums (A) ir tā pamatnes (b) un augstuma (h) funkcija tā, ka

A = (bh)/2

Eksponenciālā funkcija

Eksponenciālā funkcija ir tas, kas tiek attēlots kā f(x) = e^x. To bieži izmanto, lai parādītu strauju augšanu vai sabrukšanu.

Logaritmiskā funkcija

Logaritmiskā funkcija ir matemātiska funkcija, kas attēlo eksponenciālas apgrieztās darbības. To attēlo kā f(x) = log x.

Griestu funkcija

Griestu funkcija , kas apzīmēts kā ⌈x⌉, noapaļo reālo skaitli x līdz tuvākajam veselam skaitlim, kas ir lielāks vai vienāds ar x. Citiem vārdiem sakot, tiek atrasta mazākā veselā skaitļa vērtība, kas ir lielāka vai vienāda ar x.

Grīdas funkcija

Grīdas funkcija, kas apzīmēta kā ⌊x⌋, noapaļo reālo skaitli x uz leju līdz tuvākajam veselam skaitlim, kas ir mazāks vai vienāds ar x. Citiem vārdiem sakot, tiek atrasta lielākā veselā skaitļa vērtība, kas ir mazāka vai vienāda ar x.

Moduļa funkcija

Moduļa funkcija , kas pazīstama arī kā absolūtās vērtības funkcija, atgriež reāla skaitļa lielumu vai lielumu, neņemot vērā tā zīmi. Moduļa funkcija tiek apzīmēta kā ∣x∣, kur x ir ievades vērtība.

Signum funkcija

Signum funkcija , kas pazīstama arī kā zīmes funkcija vai signum funkcija, ir matemātiska funkcija, kas atgriež reāla skaitļa zīmi. Tas norāda, vai skaitlis ir pozitīvs, negatīvs vai nulle.

Trigonometriskās funkcijas

Trigonometriskās funkcijas ir matemātiskas funkcijas, kas saista taisnleņķa trīsstūra leņķus ar tā malu garumiem. Sešas primārās trigonometriskās funkcijas ir sine (sin), kosinuss (cos), tangenss (tan), kosekants (cosec), secant (sec) un kotangenss (cot).

Sarežģītas funkcijas

Jebkura funkcija, kurā ievades mainīgais ir sarežģīta funkcija, tiek saukta par komplekso funkciju. Komplekss skaitlis ir skaitlis, ko var attēlot kompleksajā plaknē. Iekšā kompleksais skaitlis mums ir reālais skaitlis un iedomātais skaitlis. Komplekss skaitlis (z) tiek attēlots kā, z= x + iy, un kompleksā funkcija tiek attēlota kā, f(z) = P(x, y) + iQ(x, y)

Funkciju lietojumprogrammas

Kad mēs sakām, ka mainīgais lielums y ir mainīga lieluma x funkcija, mēs norādām, ka y ir atkarīgs no x un ka y vērtību nosaka x vērtība. Šo atkarību var izteikt šādi: f = y (x).

• Apļa rādiusu var izmantot, lai aprēķinātu apļa laukumu. Rādiuss r ietekmē apgabalu A. Mēs paziņojam, ka A ir r funkcija funkciju matemātiskajā valodā. Var uzrakstīt A = f(r) =π×r²
• Sfēras tilpums V ir tās rādiusa funkcija. V = f(r) = 4/3 × r³apzīmē V atkarību no r.
• Spēks ir fiksētas masas m ķermeņa paātrinājuma funkcija. F = g(a) = m × a.

Cilvēki arī lasa:

• Saistība un funkcija
  
• Trigonometrisko funkciju domēns un diapazons
• Funkcijas diapazons
• Hiperboliskā funkcija

Funkcijas piemēri

1. piemērs: divām funkcijām f un g ir definēti kā f(x) = x ² un g(x) = ln(2x). Atrodiet salikto funkciju (gof )( x )

Risinājums:

Ņemot vērā:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln (2f (x))

kas ir map java

= ln(2x²)

= 2 ln(√2x)

Tādējādi (gof)(x) = 2 ln(√2x)

2. piemērs: atrodiet funkcijas g(t)= 6t izvadi ² + 5 plkst

• (i) t = 0
• (ii) t = 2

Risinājums:

Dotā funkcija,

g(t)= 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5(2)

g(2) = 24 + 10

g(2) = 34

3. piemērs: Taisnstūra garums ir piecas reizes lielāks par tā platumu, izsakiet taisnstūra laukumu kā tā garuma funkciju.

Risinājums:

Pieņemsim, ka taisnstūra garums ir l un taisnstūra platums ir b

Tagad

• b = l/5

Taisnstūra laukums (A) = l × l/5 = l²/5

Tādējādi taisnstūra laukums kā tā garuma funkcija ir,

A(l) = l ² /5

Praktizējiet problēmas par to, kas ir funkcija

1. Dota funkcija f(x)=3x+5

• Atrast f(2)
• Atrast f(−1)
• Nosakiet funkcijas domēnu un diapazonu.

2. Dota funkcija g(x)=x ² - 4x + 3

• Atrodiet funkcijas saknes.
• Atrodiet g(3) un g(0).
• Nosakiet funkcijas virsotni.

3. Dotas divas funkcijas f(x)=x + 2 un h(x)=2x – 3

css centrējot attēlu

• Atrodiet salikto funkciju (f ∘ h) (x)
• Novērtēt (f ∘ h)(2)

Kopsavilkums – kas ir funkcija

Funkcija matemātikā ir īpaša saistība starp ievades vērtībām (domēns) un izvades vērtībām (diapazons), kur katra ievade ir saistīta ar unikālu izvadi. Funkcijas attēlo kā y = f(x), tām ir specifiskas īpašības, un tās var vizualizēt, izmantojot sakārtotus pārus, tabulas vai grafikus. Tie ir būtiski dažādās matemātiskās problēmās, un tiem ir dažādi veidi, tostarp injicējamie (viens pret vienu), surjektīvie (uz) un bijektīvie (abi). Funkcijas var pārbaudīt, izmantojot vertikālās līnijas testu, un tās tālāk klasificē polinoma, apgrieztās, eksponenciālās, logaritmiskās un trigonometriskās funkcijās. Funkciju izpratne ietver to domēna, diapazona un to definējošo noteikumu atpazīšanu. Piemēri ietver vienkāršas lineāras funkcijas, piemēram, y = 2x + 1 un sarežģītas funkciju kompozīcijas. Funkcijas spēlē izšķirošu lomu algebrā, ģeometrijā un aprēķinos, palīdzot attēlot un analizēt matemātisko sakarību un reālās pasaules parādības.

Bieži uzdotie jautājumi par to, kas ir funkcija

Kāda ir funkcijas definīcija?

Relāciju f, kas definēta kopā A ar citu kopu B, matemātikā sauc par funkciju, ja katrai A vērtībai kopā B ir unikāla vērtība.

Kā uzrakstīt funkciju matemātikā?

Funkcija f matemātikā tiek attēlota kā f: A → B un ir definēta kā, f(x) = x + 2. Šeit katrai unikālajai x vērtībai mums ir unikāla y vērtība.

Kā pārveidot funkciju?

Mēs varam viegli pārveidot funkciju uz citām funkcijām, vienkārši veicot funkcijai pamata algebriskās darbības. Funkcijas dažādās transformācijas ir atspoguļošana, tulkošana, rotācija utt.

Kas ir racionāla funkcija?

Daļveida funkciju, kurā skaitītājs un saucējs ir polinoma funkcijas, sauc par racionālo funkciju. Daži racionālās funkcijas piemēri ir:

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), utt.

Kas ir lineāra funkcija?

Algebrisko funkciju, kurā katrs funkcijas loceklis ir vai nu konstants, vai kura jauda ir viens, sauc par lineāru funkciju. Daži lineārās funkcijas piemēri ir:

• f(x) = 2x + 3
• g(x) = x – 5 utt.

Kas ir funkcijas domēns un kodomēns?

Ja funkciju definējam kā, y = f(x). Tad x domēns ir visas x vērtības, kurām y iegūst unikālu vērtību. Un y kopdomēns ir visu y vērtību kopa katrai x vērtībai.

Kā jūs identificējat funkciju matemātikā?

Ja jebkurai relācijas domēna ievades vērtībai (x) ir vairāk nekā viens attēls (y), tad šīs attiecības nekad nevar būt funkcija. Tātad, ja x vērtība tiek atkārtota sakārtotajā pārī, tā nekad nav funkcija.