Leņķi mēra grādos (°) un radiānos. Tas ir izveidots starp divām blakus esošajām daudzstūra malām. Katram daudzstūrim ir dažādas malas un atšķirīgs leņķu skaits. Formula leņķu atrašanai grādos ir noderīga ģeometrijā un trigonometrijā. Ir svarīgi saprast citus matemātikas jēdzienus, piemēram, loku, apļa centrālo leņķi utt.

1. Pilns aplis = 360°
2. Taisna līnija = 180°
3. Pusaplis = 180°
4. A Ceturkšņa aplis = 90°

Leņķu aprēķināšana grādos

Ir trīs dažādas metodes leņķu atrašanai grādos, kas ir šādas:

1. Izmantojot aizsargu D
2. Izmantojot Pitagora teorēmu un trigonometrijas funkciju taisnleņķa trīsstūrī
3. Izmantojot leņķu summas formulu
4. Apļa centrālais leņķis

Izmantojot aizsargu D

Aizsargs ir lineāla vai skalas veids, ko izmanto attāluma mērīšanai centimetros vai milimetros. Leņķu mērīšanai izmantotais aizsargs ir “D” formā ar leņķu vērtību no 0 līdz 180° no jebkura virziena (pa labi vai pa kreisi). Lai izmērītu leņķi, ass ir jāsaskaņo ar līniju D. Aizsarga vidējais aplis ir izlīdzināts ar mērītā leņķa virsotni. Stari gar leņķa virsotni palīdzēs atrast leņķi grādos.

Izmantojot Pitagora teorēmu un trigonometrijas funkciju taisnleņķa trīsstūrī

Trigonometrijā ir sešas funkcijas, sine, cos, cosec, iedegums, bērnu gultiņa, un sek. Taisnleņķa trīsstūrim ir trīs malas: pamatne, perpendikula un hipotenūza.

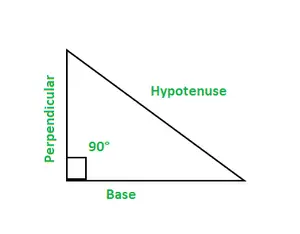
Pamatne: tā ir blakus mala 90° leņķim. Perpendikula: tā ir arī blakus mala 90° leņķim. Hipotenūza: tā ir mala, kas ir pretēja 90° leņķim.

Taisnleņķa trīsstūris kā viens no leņķiem ir attēlots ar 90° leņķi. Trijstūra leņķu kopējā summa ir 180°.

Cosecθ: to attēlo kā hipotenūzu, kas dalīta ar perpendikulāru.

Cosecθ =

Cotθ: to attēlo kā bāzi, kas dalīta ar perpendikulu.

Cotθ =

Pārējās trigonometriskās funkcijas ir attēlotas šādi:

sinθ =

Cosθ =

tanθ =

secθ =

Cosecθ var attēlot arī kā 1/sinθ

secθ var attēlot arī kā 1/ cosθ

Cotθ var attēlot arī kā 1/tanθ

kur,

Θ ir leņķis

Pitagora teorēma

Ja ir zināmas taisnā leņķa divas malas, mēs varam viegli aprēķināt taisnleņķa trijstūra trešo malu. Taisnleņķa trijstūrī Pitagora teorēmu nosaka:

(hipotenūza)²= (Bāze)²+ (perpendikulāri)²

Leņķu summas formula

Leņķu summa attiecas uz daudzstūra iekšējo leņķu kopējo summu, kas veidojas starp abām malām. Ja daudzstūrim ir sešas malas, tad ir aptuveni seši leņķi. Tas palīdz atrast leņķi, ja ir zināmi citi leņķi un daudzstūra leņķu summa.

Formulu daudzstūra leņķu kopsummas atrašanai nosaka:

Kopējā leņķu summa = 180 (n–2)

kur,

n ir daudzstūra malu skaits

rakstzīme uz virkni java

Piemērs:

• Ja n = 4,

Kopējā leņķu summa = 180 (4–2)

= 180 (2)

= 360°

Ja n = 5,

Kopējā leņķu summa = 180 (5–2)

= 180 (3)

= 540°

• Ja n = 6

Kopējā leņķu summa = 180 (6–2)

= 180 (4)

= 720°

Apļa centrālais leņķis

Aplis ir apaļas formas figūra, kuras robeža atrodas vienādā attālumā no centra punkta. Attālums starp centra punktu un robežu ir pazīstams kā apļa rādiuss. Leņķi, ko veido divi apļa rādiusi, sauc par centrālo leņķi. Apļa centrālā leņķa vērtība ir no 0 līdz 360 grādiem.

Formulu apļa centra leņķa aprēķināšanai dod:

Loka garums = 2πr × (θ/360)

Θ = 360L/2pr

kur,

r ir apļa rādiuss

AB ir loka

Teta ir leņķis grādos.

L = loka garums

Problēmu paraugi

1. jautājums: atrast centrālo leņķi aplim ar rādiusu 2m ar loka garumu 4m?

Risinājums :

Formulu apļa centra leņķa aprēķināšanai dod:

Θ = 360L/2pr

kur,

r ir apļa rādiuss

Teta ir leņķis grādos.

L = loka garums

Θ = leņķis grādos

r = 2 m

L = 4 m

Θ = 360 × 4 /2 × π × 2

Θ = 114,6°

Tādējādi apļa centrālais leņķis ir 114,6°.

2. jautājums: atrast centrālo leņķi aplim ar rādiusu 10 cm ar loka garumu 18 cm?

Risinājums :

Formulu apļa centra leņķa aprēķināšanai dod:

Θ = 360L/2pr

kur,

r ir apļa rādiuss

Teta ir leņķis grādos.

L = loka garums

r = 10 cm

L = 18 cm

Θ = leņķis grādos

Θ = 360 × 18 /2 × π × 10

Θ = 103,13°

Tādējādi apļa centrālais leņķis ir 103,13°.

3. jautājums: atrast paralelograma leņķi, ja pārējie trīs leņķi ir 80°, 95° un 105°?

Risinājums :

Paralelogramam ir četras malas ar kopējo leņķu summu 360°.

Formula leņķu summas atrašanai = 180 (n – 2)

kur,

n ir daudzstūra malu skaits

Šeit n = 4,

Kopējā leņķu summa = 180 (4–2)

= 180 (2)

= 360°

Kopējā summa = 1. leņķis + 2. leņķis + 3. leņķis + 4. leņķis

360 = 80+ 95+ 105+ 4. leņķis

360 = 280 + 4. leņķis

4. leņķis = 360–280

Leņķis 4 = 80°

4. jautājums: atrodiet dotajā attēlā leņķi A.

Risinājums :

Dots: Hipotenūza = 12

Perpendikulāri = 6

Trigonometrijas funkciju leņķa aprēķināšanai nosaka:

sinA = 6/12

A = 30°

5. jautājums: atrodiet dotajā attēlā leņķi A.

Risinājums :

Dots: hipotenūza = 10

Bāze = 5

Trigonometrijas funkciju leņķa aprēķināšanai nosaka:

CosA = 5/10

A = 60°

6. jautājums. Atrodiet piecstūra leņķi, ja pārējie četri leņķi ir 115°, 100°, 105° un 100°?

Risinājums :

Piecstūrī ir piecas malas ar kopējo leņķu summu 540°.

Formula leņķu summas atrašanai = 180 (n – 2)

kur,

n ir daudzstūra malu skaits

āmrija vs āpsis

Šeit n = 5,

Kopējā leņķu summa = 180 (5–2)

= 180 (3)

= 540°

Kopējā summa = 1. leņķis + 2. leņķis + 3. leņķis + 4. leņķis + 5. leņķis

540 = 115° + 100° + 105° + 100° + leņķis 5

540 = 420 + 5. leņķis

5. leņķis = 540–420

Leņķis 5 = 120°

7. jautājums: atrodiet dotajā attēlā leņķi A.

Risinājums :

Dots: Bāze = √3

Perpendikulārs = 1

Trigonometrijas funkciju leņķa aprēķināšanai nosaka:

tanθ =

tanθ = 1/√3

A = 30°

8. jautājums: atrast paralelograma leņķi, ja pārējie trīs leņķi ir 100°, 70° un 80°?

Risinājums :

Paralelogramam ir četras malas ar kopējo leņķu summu 360°.

Formula leņķu summas atrašanai = 180 (n – 2)

kur,

n ir daudzstūra malu skaits

Šeit n = 4,

Kopējā leņķu summa = 180 (4–2)

= 180 (2)

= 360°

Kopējā summa = 1. leņķis + 2. leņķis + 3. leņķis + 4. leņķis

360 = 100 + 70 + 80 + 4. leņķis

360 = 250 + 4. leņķis

4. leņķis = 360–250

Leņķis 4 = 110°

Tādējādi otrs leņķis ir 110°.

9. jautājums. Atrodiet sešstūra leņķi, ja pārējie pieci leņķi ir 120°, 115°, 110°, 125° un 105°?

Risinājums :

Sešstūrī ir sešas malas ar kopējo leņķu summu 720°.

Formula leņķu summas atrašanai = 180 (6–2)

kur,

n ir daudzstūra malu skaits

Šeit n = 6,

Kopējā leņķu summa = 180 (6–2)

= 180 (4)

= 720°

Kopējā summa = 1. leņķis + 2. leņķis + 3. leņķis + 4. leņķis + 5. leņķis + 6. leņķis

720 = 120 + 115 + 110 + 125 + 105 + leņķis 6

720 = 575 + 6. leņķis

6. leņķis = 720–575

Leņķis 6 = 145°

Tādējādi sešstūra sestais leņķis ir 145°.