logo

TechCodeview

Apgabala formulas

Apgabala formulas dažādiem objektiem ir formulas, kas tiek izmantotas, lai atrastu dažādu objektu laukumu. Platība ir telpa, ko aizņem jebkuras figūras robeža. Dažādu ģeometrisku formu laukumu formulas ir atkarīgas no dažādiem parametriem, piemēram, dažādu ģeometrisku formu izmēriem, augstuma un rādiusa. Ģeometriskās formas ir divu veidu:

  • Divdimensiju formas (2-D formas)
  • Trīsdimensiju formas (3-D formas)

Šajā rakstā mēs detalizēti uzzināsim par laukumu formulām dažādām 2-D un 3-D formām, piemēram, taisnstūra laukumu, kvadrāta laukumu, apļa laukumu, kuba laukumu utt.



Satura rādītājs

Kas ir apgabals?

Telpu, ko aizņem figūras robeža, sauc par figūras laukumu. To mēra kvadrāta vienībā. SI vienība laukuma mērīšanai ir m2. Platība tiek izmantota dažādās matemātiskās koncepcijās un tiek izmantota arī reālās dzīves scenārijos, piemēram, lai atrastu telpas laukumu, laukuma tabulu utt.

Kas ir apgabala formulas?

Platības formulas ir būtiski rīki, ko izmanto matemātikā, lai aprēķinātu telpas apjomu, ko aptver dažādas divdimensiju formas. Šīs formulas var izmantot, lai atrastu ģeometrisko laukumu figūras, piemēram, kvadrāti, taisnstūri, apļi, trīsstūri, trapeces un elipses. Izmantojot šīs formulas, mēs varam precīzi aprēķināt dažādu formu laukumu, ļaujot mums atrisināt reālas problēmas un veikt svarīgus aprēķinus.



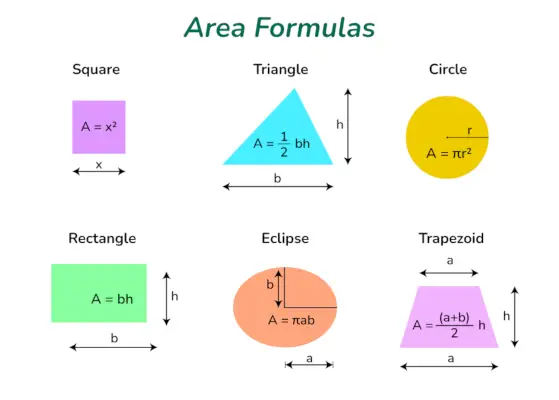
Platība-Formulas

Apgabala formulas

Kas ir 2D formas?

Formas, kurām ir tikai divas dimensijas, sauc par 2-D formas . Tie ir zīmēti 2-D telpā un ir atkarīgi no 2 parametri, parasti garums (l) un platums (b). Dažādas 2-D formas ir, Taisnstūris, kvadrāts, trīsstūris, apļi un citi.

2D formu formulas laukums

2D formu apgabala formulas ir formula, ko izmanto, lai iemīļotu dažādu 2D formu laukumu, piemēram, trīsstūra laukumu, kvadrāta laukumu, taisnstūra laukumu, romba laukumu utt. Šīs apgabalu formulas tiek plaši izmantotas matemātikā, lai atrisināt dažādas ģeometriskas problēmas. Dažādas apgabalu formulas dažādām formām ir,



Taisnstūra laukuma formula

Taisnstūris ir 2 dimensiju figūra kas ir četrstūris, t.i., tam ir četras malas tā pretējās malas ir paralēlas un vienādas. Visi taisnstūra leņķi ir vienādi, un to mērs ir 90 grādi. Taisnstūra diagonāles ir vienādas un ir viena otrai perpendikulāras bisektrise.

Taisnstūra laukuma aprēķināšanas formula ir ar garumu un l un platums b ir,

  • Taisnstūra laukums (A) = l × b kvadrāta vienības

Kvadrāta laukuma formula

Kvadrāts ir divdimensiju figūra, kas ir četrstūris, t.i., tai ir četras malas, tā pretējās malas ir paralēlas un visas četras kvadrāta malas ir vienādas. Visi kvadrāta leņķi ir vienādi, un to mērs ir 90 grādi. Kvadrāta diagonāles ir vienādas un ir viena otrai perpendikulāras bisektrise.

Formula kvadrāta ar malu laukuma aprēķināšanai a ir,

  • Kvadrāta laukums (A) = a 2 kv vienības

Trijstūra laukuma formula

Trīsstūris ir vienkāršākais daudzstūris, kas izveidots, savienojot trīs taisnas līnijas. Kā norāda nosaukums, tas ir daudzstūris ar trim leņķiem. Trijstūra visu malu garumu summa ir trijstūra perimetrs, un telpa trijstūra perimetrā ir trijstūra laukums.

sql servera pivot

Formula trijstūra ar pamatni laukuma aprēķināšanai b ir un augstums h ir,

  • Trijstūra laukums (A) = 1/2 × bh kv. vienības

Apļa zonas formula

Aplis ir ģeometriska figūra bez taisnas līnijas. Tas ir punkta lokuss, kas vienmēr atrodas nemainīgā attālumā no fiksētā punkta. Fiksētais punkts sauc par apļa centru, un fiksētais attālums ir apļa rādiuss.

Formula aprēķināšanai apļa laukums ar r kā apļa rādiusu,

  • Apļa laukums (A) = πr 2 kv vienības

Paralēlogrammas laukuma formula

Paralēlogramma ir 2-D figūra kurā pretējās malas ir paralēlas un vienādas. Formula paralelograma laukuma ar pamatni aprēķināšanai b un augstums h ir,

  • Paralelogrammas laukums (A) = bh kv. vienības

Romba apgabala formula

Rombs ir četrstūris, kura visas četras malas ir vienādas un paralēlas, bet ne visi leņķi ir vienādi. Formula romba laukuma ar diagonāli aprēķināšanai d 1 un d 2 ir,

  • Romba laukums (A) = 1/2 × d 1 × d 2 kv vienības

Trapecveida laukuma formula

Trapecveida ir cits nosaukums trapece . Tas ir četrstūris, kura pretējās malas ir paralēlas. Formula trapeces ar paralēlām malām laukuma aprēķināšanai a un b un augstums h ir,

  • Trapecveida (A) laukums = 1/2(a +b)h kv.vienības

Elipses laukuma formula

Elipse ir divdimensiju forma, un to veido konusveida daļas. Formula elipses laukuma aprēķināšanai ar asi as a un b ir,

  • Elipses laukums (A) = πab kvadrātvienības

Pusloka laukuma formula

Pusaplis ir 2-D figūra, kas ir puse no apļa. Formula, lai aprēķinātu pusloka laukumu ar rādiusu r, ir:

  • Pusloka laukums (A) = 1/4(πr 2 ) kv

Apgabalu formulu tabula

Formulas dažādu 2-D figūru laukumiem ir pievienotas tabulā, kas pievienota zemāk,

Skaitļi

Formula

Mainīgie lielumi

Taisnstūris

Laukums = l × b
  • l ir garums
  • b ir platums

Kvadrāts

Platība = a2

a ir kvadrāta mala

Trīsstūris

Platība = 1/2 × bh
  • b ir bāze
  • h ir augstums

Aplis

Laukums = πr2

r ir apļa rādiuss

Trapecveida

Laukums = 1/2×(a+b)h
  • a ir pirmā bāze
  • b ir otrā bāze

Rombs

Platība = 1/2×d1×d2
  • d1ir viena diagonāle
  • d2ir otrā diagonāle

Paralēlogramma

Platība = b × h
  • b ir bāze
  • h ir augstums

Elipse

Platība = πab
  • a ir galvenās ass rādiuss
  • b ir mazās ass rādiuss

Kas ir 3D formas?

3-D formas ir formas, kas tiek zīmētas 3-D telpās. Viņiem ir 3 izmēri, kas ir to parametri. Šo formu laukums ir atkarīgs no 3-D formu garuma, platuma un augstuma. Dažādas trīsdimensiju formas ir kubs, kubisks, cilindrs, konuss, sfēra un citas. 3-D formu laukums ir divās kategorijās: izliektās virsmas laukums (sānu virsmas laukums){CSA} un kopējais virsmas laukums (TSA). CSA ir visas 3-D formu izliektās virsmas laukums, un TSA ir visu trīsdimensiju formu virsmu laukums.

3D formu formulas laukums

3-D formu laukums ir vieta, ko aizņem visas figūras sejas. To mēra vienībās2. Laukuma SI vienība ir m2. The kuba laukums , kuboīda laukums , cilindra laukums, konusa laukums un citi ir 3D formu apgabalā. Tālāk pievienotajā tabulā parādītas dažādu 3-D figūru formulas.

arraylist.sort

Formas apgabals

Virsmas laukums

Parametri

Kuba laukums

6a2

a ir malas garums

Kuboīda apgabals

2 (lb + lh + bh)
  • l ir malas garums
  • b ir malas platums
  • h ir malas augstums

Konusa apgabals

πr(r + l)
  • r = apļveida pamatnes rādiuss
  • l = slīpuma augstums

Cilindra laukums

2π(r + h)
  • r = apļveida pamatnes rādiuss
  • h = cilindra augstums

Sfēras apgabals

4πr2

r ir sfēras rādiuss

Puslodes apgabals

3πr2

r ir puslodes rādiuss

Taisnstūra prizmas laukums

2 (wl + hl + hw)
  • l ir malas garums
  • w ir malas platums
  • h ir malas augstums

Tāpat pārbaudiet

  • Platības un perimetra formulas
  • Virsmas laukuma formulas

Apgabalu formulu piemēri

1. piemērs: atrodiet laukumu taisnstūram, kura garums ir 5 cm un platums 2 cm.

Risinājums:

Ņemot vērā,

  • Taisnstūra garums (l) = 5 cm
  • Taisnstūra (b) platums = 2 cm

Taisnstūra laukums (A) = l × b

A = 5 cm × 2 cm
= 10 cm2

2. piemērs: Atrodiet kvadrātveida parka laukumu, kura mala ir 4 m.

Risinājums:

Ņemot vērā,

  • Laukuma (a) mala = 4 m

Kvadrāta laukums = a2
= (4)2= 16 m2

Tādējādi laukuma parka platība ir 16 m2

3. piemērs: atrodiet trīsstūrveida plāksnes laukumu, kuras augstums ir 6 cm un pamatne ir 6 cm.

Risinājums:

Ņemot vērā,

  • Trīsstūra augstums (h) = 6 cm
  • Trijstūra (b) pamatne = 8 cm

Trijstūra laukums (A) = 1/2 (b × h)

A = 1/2 (8 × 6)
= 48/2 = 24 cm2

Trīsstūrveida plāksnes laukums ir 24 cm2

4. piemērs: atrodiet apļveida diska laukumu ar rādiusu 1,4 cm.

Risinājums:

Ņemot vērā,

  • Apļa rādiuss (r) = 1,4 cm

Apļa laukums(A) = πr2

A = π(1,4)2
= 22/7 (1,4) (1,4) = (4,4) (1,4)
= 6,16 cm2

Apļveida diska laukums ir 6,16 cm2

Bieži uzdotie jautājumi par apgabala formulām

Kas ir apgabala formulas?

Laukuma formulas ir formulas, kuras izmanto, lai atrastu jebkuras figūras laukumu. To izmanto, lai noteiktu figūras aizņemtās vietas daudzumu. Parasti apgabals tiek apzīmēts ar burtu “A”. un tiek mērīts vienībās2, t.i., cm2, m2utt.

Kas ir laukuma formula kvadrātam?

Kvadrāta laukuma formula ir formula kvadrāta aizņemtās vietas aprēķināšanai. Kvadrāta laukuma aprēķināšanas formula ir šāda:

Kvadrāta laukums = (malā) 2

Kas ir taisnstūra laukuma formula?

Taisnstūra laukuma formula ir formula taisnstūra aizņemtās vietas aprēķināšanai. Formula taisnstūra laukuma aprēķināšanai ir:

Taisnstūra laukums = garums × platums

java apmācība iesācējiem

Kas ir trīsstūra laukuma formula?

Trijstūra laukuma formula ir formula, lai aprēķinātu trijstūra aizņemto vietu. Formula trijstūra laukuma aprēķināšanai ir:

Trijstūra laukums = 1/2 (pamatne × augstums)

Kas ir apļa apgabala formula?

Apļa laukuma formula ir formula, lai aprēķinātu apļa aizņemto vietu. Formula apļa laukuma aprēķināšanai ir:

Apļa laukums = π(rādiuss) 2

Kas ir četrstūra laukuma formula?

Formula četrstūra laukuma aprēķināšanai,

Četrstūra laukums = 1/2 × diagonāle 1 × Diagonāli 2

Kas ir trīsstūrveida prizmas laukuma formula?

Trīsstūrveida prizmas laukuma formula ir:

Trīsstūrveida prizmas laukums = (pamatnes perimetrs × prizmas garums) + 2 × pamatnes laukums

Kas ir daudzstūra laukuma formula?

Daudzstūra laukuma aprēķināšanas formula ir:

Daudzstūra laukums = 1/2 × (perimetrs × apotēms)

Kas ir taisnleņķa trīsstūra laukuma formula?

Taisnleņķa trijstūra laukuma formula ir,

Taisnā trijstūra laukums = 1/2 × perpendikulārs × pamatne

Kas ir Pentagona apgabala formula?

Pentagona laukuma formula ir:

Pentagona laukums = 1/2 × perimetrs × apotēms