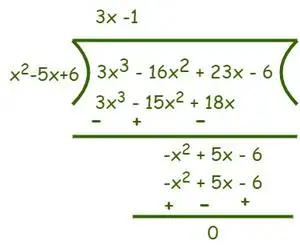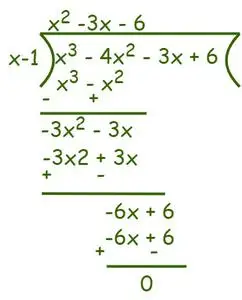Kubiskais vienādojums ir matemātisks vienādojums, kurā 3. pakāpes polinoms ir pielīdzināts konstantei vai citam polinomam ar maksimālo 2. pakāpi. Kubiskā vienādojuma standarta attēlojums ir cirvis ³ +bx ² +cx+d = 0 kur a, b, c un d ir reāli skaitļi. Daži kubiskā vienādojuma piemēri ir x ³ - 4x ² + 15x – 9 = 0, 2x ³ - 4x ² = 0 utt.

Satura rādītājs

• Polinoma definīcija
• Vienādojuma pakāpe
• Kubiskā vienādojuma definīcija
• Kā atrisināt kubiskos vienādojumus?
• Kubisko vienādojumu risināšana
• Kubiskā vienādojuma risināšana, izmantojot faktorus
• Kubiskā vienādojuma atrisināšana, izmantojot grafisko metodi
• Uzdevumi, kas balstīti uz kubisko vienādojumu risināšanu
• Praktizējiet kubisko vienādojumu risināšanas uzdevumus

Lai uzzinātu, kā atrisināt kubiskos vienādojumus, mums vispirms jāapgūst polinomi, polinoma pakāpe un citi. Šajā rakstā mēs detalizēti uzzināsim par polinomiem, polinoma vienādojumiem, kubisko vienādojumu risināšanu vai kubisko vienādojumu atrisināšanu un citiem.

Polinoma definīcija

Polinomu definē šādi,

A polinoms ir algebriska izteiksme, kurā mainīgā jauda ir nenegatīvs vesels skaitlis. Polinoma vispārējā forma ir a₀xⁿ+ a₁x^n-1+ a₂x^n-2+… + a_n. Atkarībā no mainīgā maksimālās jaudas polinomu var klasificēt kā monomu, binomiālu, trinomu un tā tālāk.

Kas ir vienādojums?

Vienādojums ir definēts šādi,

Vienādojums ir polinoms, kas tiek pielīdzināts skaitliskai vērtībai vai jebkuram citam polinomam. Piemēram, x + 2 ir polinoms, bet x + 2 = 5 ir vienādojums. Tāpat 2x + 3 = x + 1 ir arī vienādojums, savukārt 2x + 3 un x + 1 ir polinomi atsevišķi.

Vienādojuma pakāpe

Vienādojuma pakāpes definīcija ir norādīta zemāk:

Vienādojuma pakāpe ir definēta kā maksimālā jauda, ​​kas piemīt mainīgajam vienādojumā.

Pamatojoties uz vienādojuma pakāpi, vienādojumu var klasificēt šādi:

• Lineārais vienādojums
• Kvadrātvienādojums
• Kubiskais vienādojums
• Bikvadrātiskais vienādojums

Lineārais vienādojums

Vienādojumu, kurā mainīgā maksimālā jauda ir 1, sauc par lineāro vienādojumu.

• Piemēram, 3x +1 = 0

Kvadrātiskais polinoms

Vienādojums, kurā mainīgā maksimālā jauda ir 2, ir kvadrātvienādojums.

• Piemēram, 3x²+x+1 = 0

Kubiskais vienādojums

Vienādojumu, kurā mainīgā maksimālā jauda ir 3, sauc par kubisko vienādojumu.

• Piemēram, 5x³+3x²+x+1 = 0

Bikvadrātiskais polinoms

Vienādojumu, kurā mainīgā maksimālā jauda ir 4, sauc par bikvadrātisku polinomu vai kvartisku polinomu.

• Piemēram, 5x⁴+4x³+3x²+2x+1 = 0

Kubiskā vienādojuma definīcija

Kubiskais vienādojums ir algebrisks vienādojums, kurā polinoma augstākā pakāpe ir 3. Daži kubisko vienādojumu piemēri ir 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 utt.

Kubiskā vienādojuma vispārējā forma ir:

cirvis ³ + bx ² + cx + d = 0, a ≠ 0

kur,

• a, b, un c ir mainīgā lieluma koeficienti un to eksponenāti un d ir konstante, un
• a, b, c un d ir reāli skaitļi.

Kā atrisināt kubiskos vienādojumus?

Kubiskais vienādojums ir vienādojums ar trešo pakāpi. Tam ir trīs risinājumi, un to var viegli atrisināt, veicot tālāk norādītās darbības,

1. darbība: Atrodiet vienu kubiskā vienādojuma risinājumu ar sitienu un izmēģiniet metodi. Pieņemsim, ka mums ir kubiskais vienādojums P(x), pēc tam atrodiet jebkuram x = a, P(a) = 0, pieņemot, ka x = 0, ±1, ±2, ±3, … un tā.

2. darbība: Kad mēs iegūstam, P(a) = 0, atrodam koeficientu (x – a) no P(x)

3. darbība: Sadaliet P(x) ar (x – a), lai iegūtu kvadrātvienādojumu, sakot Q(x), izmantojot polinoma dalīšanu.

4. darbība: Faktorizējiet kvadrātvienādojumu Q(x), lai iegūtu faktorus kā (x – b) un (x – c).

5. darbība: (x – a), (x – b) un (x – c) ir P(x) faktori, un, atrisinot katru faktoru, mēs iegūstam vienādojuma saknes kā, a, b un c.

Uzziniet vairāk par, Dalīšanas polinoms

Kubisko vienādojumu risināšana

A Kubiskais vienādojums var atrisināt ar divām metodēm

• Samazinot to kvadrātvienādojumā un pēc tam atrisinot ar faktoringu vai kvadrātisko formulu
• Ar grafisko metodi

A Kubiskais vienādojums ir trīs saknes. Šīs saknes var būt reālas vai iedomātas. Var būt arī atšķirīgas saknes vai divas vienādas un viena atšķirīga sakne un visas trīs vienādas saknes.

Jāatzīmē, ka jebkuram vienādojumam, ieskaitot Kubiskie vienādojumi , vienādojums vienmēr ir jāsakārto tā standarta formā pirms vienādojuma atrisināšanas.

Piemēram, ja dotais vienādojums ir 2x²-5 = x + 4/x, tad mums tas ir jāpārkārto standarta formā, t.i., 2x³-x²-5x-4 = 0. Tagad mēs varam atrisināt vienādojumu, izmantojot jebkuru piemērotu metodi.

Kubiskā vienādojuma risināšana, izmantojot faktorus

Kubiskā vienādojuma risinājums, izmantojot faktoru teorēmu, ir izskaidrots, izmantojot tālāk pievienoto piemēru,

Piemērs: Atrodiet vienādojuma f(x) = 3x saknes ³ -16x ² + 23x − 6 = 0.

Risinājums:

Dotā izteiksme: f(x) = 3x³-16x²+ 23x − 6 = 0

Pirmkārt, faktorizējiet polinomu, lai iegūtu saknes

Tā kā konstante ir -6, iespējamie faktori ir 1, 2, 3, 6

f(1) = 3–16 + 23–6 ≠ 0

f(2) = 24–64 + 46–6 = 0

f(3) = 81–144 + 69–6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

Mēs to zinām, saskaņā ar Faktoru teorēma ja f(a) = 0, tad (x-a) ir f(x) koeficients

Tātad (x – 2) un (x – 3) ir f(x) faktori. Tāpēc (x – 2) un (x – 3) reizinājums būs arī koeficients f(x). Tagad, lai atrastu atlikušos faktorus, izmantojiet garās dalīšanas metodi un sadaliet f(x) ar (x – 2) un (x – 3) reizinājumu.

Tādējādi dalītājs = (x – 2) (x – 3) = (x²– 5x + 6) un dividende = 3x³-16x²+ 23x − 6. Tagad sadaliet, kā parādīts zemāk,

Pēc dalīšanas iegūstam (3x-1) kā koeficientu un atlikumu ir 0. Tagad kā Dalīšanas algoritms mēs to zinām Dividende = dalītājs × koeficients + atlikums.

⇒ f(x) = (3x³−16x²+ 23x − 6) = (x²– 5x + 6) (3x-1)

Tā kā f(x) = 0

⇒ (x²– 5x + 6) (3x-1) = 0

⇒ x²– 5x + 6 = 0 vai 3x-1 = 0

Kā noņemt pirmo rakstzīmi programmā Excel

Tagad mēs ņemsim 3x-1 = 0 ⇒ x = 1/3, jo mēs jau zinām divas saknes no x²– 5x + 6, kas ir 2 un 3

Tātad,

Dotā saknes Kubiskais vienādojums ir 1/3, 2 un 3.

Kubiskā vienādojuma atrisināšana, izmantojot grafisko metodi

Kubiskais vienādojums tiek atrisināts grafiski, ja jūs nevarat atrisināt doto vienādojumu, izmantojot citus paņēmienus. Tātad, mums ir nepieciešams precīzs dotā kubiskā vienādojuma zīmējums. Vienādojuma saknes ir punkts(-i), kurā(-i) grafiks šķērso X asi, ja vienādojums ir x izteiksmē un, ja vienādojums ir y izteiksmē, tad vienādojuma saknes ir punkti, kuros grafiks sagriež Y asi.

Kubiskā vienādojuma reālo atrisinājumu skaits ir vienāds ar to, cik reižu kubiskā vienādojuma grafiks šķērso X asi.

Piemērs: Atrodiet vienādojuma f(x) = x saknes ³ - 4x ² − 9x + 36 = 0, izmantojot grafisko metodi.

Risinājums:

Dotā izteiksme: f(x) = x³- 4x²− 9x + 36 = 0.

Tagad vienkārši aizstājiet x izlases vērtības dotās funkcijas diagrammā:

x	-4 virkne java metodēs	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

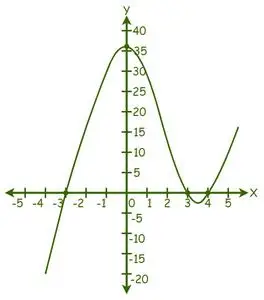
Redzams, ka grafiks ir nogriezis X asi 3 punktos, tāpēc ir 3 reāli risinājumi.

No diagrammas risinājumi ir šādi: x = -3, x = 3 un x = 4.

Tādējādi dotā vienādojuma saknes ir -3, 3 un 4.

Lasīt vairāk,

• Lineārais vienādojums
• Kvadrātvienādojuma atrisināšana
• Faktoringa polinomi

Uzdevumi, kas balstīti uz kubisko vienādojumu risināšanu

1. uzdevums: atrodiet f(x) = x saknes ³ - 4x ² -3x + 6 = 0.

Risinājums:

Dotā izteiksme: f(x) = x³- 4x²-3x + 6 = 0.

Pirmkārt, faktorizējiet polinomu, lai iegūtu saknes.

Tā kā konstante ir +6, iespējamie faktori ir 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 - 144 -18 + 6 = -48 ≠ 0

Tātad, saskaņā ar Faktoru teorēma (x – 1) ir dotā vienādojuma koeficients. Tagad, lai atrastu atlikušos faktorus, izmantojiet garās dalīšanas metodi.

Saskaņā ar Dalīšanas algoritms mēs varam rakstīt,

Tātad, f(x) = x³- 4x²-3x + 6 = (x - 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 vai (x²– 3x – 6) = 0

Mēs zinām, ka kvadrātvienādojuma saknes cirvis²+ bx + c = 0 ir,

x = [-b ± √(b²-4ac)]/2a

Tādējādi priekš (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Tādējādi dotā kubiskā vienādojuma saknes ir 1, (3+√33)/2 un (3–√33)/2.

2. uzdevums: atrodiet vienādojuma f(x) = 4x saknes ³ - 10x ² + 4x = 0.

Risinājums:

Dotā izteiksme: f(x) = 4x³- 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 vai 4x - 2 = 0, x - 2 = 0

⇒ x = 0 vai x = 1/2 vai x = 2

Tādējādi dotā vienādojuma saknes ir 0, 1/2 un 2.

3. uzdevums: atrodiet vienādojuma f(x) = x saknes ³ + 3x ² + x + 3 = 0.

Risinājums:

Dotā izteiksme: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1 (x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 vai x²+1 = 0

⇒ x = -3, ±i

Tātad dotajam vienādojumam ir reāla sakne, t.i., -3, un divas iedomātas saknes, t.i., ±i.

4. uzdevums: atrodiet vienādojuma f(x) = x saknes ³ - 7x ² – x + 7 = 0.

Risinājums:

Dotie izteicieni,

f(x) = x³- 3x²– 5x + 7 = 0

Vispirms faktorizē vienādojumu f(x): x³- 3x²– 5x + 7 = 0

To var ieskaitīt (x-7) (x+1) (x-1) = 0

Pēc polinoma faktorēšanas mēs varam atrast saknes, pielīdzinot katru faktoru nullei. Piemēram:

• x – 7 = 0, tātad x = 7
• x + 1 = 0, tātad x = -1
• x – 1 = 0, tātad x = 1

Tātad vienādojuma f(x) saknes: x³- 3x²– 5x + 7 = 0 are

• x = 7
• x = -1
• x = 1

5. uzdevums: atrodiet vienādojuma f(x) = x saknes ³ - 6x ² + 11x − 6 = 0, izmantojot grafisko metodi.

Risinājums:

Dotā izteiksme: f(x) = x³- 6x²+ 11x − 6 = 0.

Tagad vienkārši aizstājiet x izlases vērtības dotās funkcijas diagrammā:

x noņemot pēdējo commit git	1	2	3	4	5
f(x)	0	0	0	6	24

Redzams, ka grafiks ir nogriezis X asi 3 punktos, tāpēc ir 3 reāli risinājumi.

No diagrammas risinājumi ir šādi: x = 1, x = 2 un x = 3.

Tādējādi dotā vienādojuma saknes ir 1, 2 un 3.

Praktizējiet kubisko vienādojumu risināšanas uzdevumus

Tālāk ir pievienotas dažādas ar kubiskajiem vienādojumiem saistītas prakses problēmas. Atrisiniet šīs problēmas, lai pilnībā izprastu jēdzienu Kā atrisināt kubisko vienādojumu?

P1. Atrisiniet kubisko vienādojumu, 3x³+ 2x²– 11x + 7 = 0.

P2. Atrodiet kubiskā vienādojuma saknes, 4x³- 12x²+ 17 = 0.

P3. Atrisiniet kubisko vienādojumu, x³+ 4x²– x + 3 = 0, izmantojot grafisko metodi.

P4. Atrodiet skaitli, kas atbilst, -9x³+ 11x²– 8x + 2 = 0.

Bieži uzdotie jautājumi par kubisko vienādojumu risināšanu

1. Kas ir kubiskie vienādojumi?

Kubiskie vienādojumi ir algebriskie vienādojumi, kuros mainīgā maksimālā jauda ir 3

2. Kā faktorēt kubisko vienādojumu?

Kubisko vienādojumu var faktorēt divos veidos. Pirmkārt, ņemot no dotā kubiskā vienādojuma kopīgu lineāru izteiksmi, tad kā reizinājumu iegūsim lineāro un kvadrātisko izteiksmi. Šo kvadrātvienādojumu var vēl vairāk faktorizēt, lai iegūtu visus faktorus. Otrā metode ir atrast dotā kubiskā vienādojuma nulli, liekot nejaušas vērtības. Vērtība, kurai vienādojuma vērtība ir nulle, būs viena no dotā kubiskā vienādojuma nullēm. Tagad, izmantojot faktoru teorēmu, izveidojiet lineāru izteiksmi, teiksim x-a un sadaliet doto kubiskā vienādojumu ar šo izteiksmi, kas iegūs kvadrātvienādojumu kā koeficientu. Šo iegūto kvadrātvienādojumu var tālāk faktorizēt, lai iegūtu visus faktorus.

3. Kā grafiski atrisināt kubisko vienādojumu?

Lai atrisinātu kubisko vienādojumu, grafiski ievietojiet x nejaušās vērtības dotajā kubiskajā vienādojumā un atrisinātu, jūs iegūsit y vērtības. Atzīmējiet šīs iegūtās vērtības grafikā. Atrodiet koordinātas, kurās grafiks krustojas ar x asi. Šīs koordinātas ir kubiskā vienādojuma atrisinājums.

4. Vai visus kubiskos vienādojumus var atrisināt precīzi?

Jebkuram vienādojumam, kuram ir nepāra jauda, ​​ir jābūt vienai reālai saknei. Tādējādi kubiskā vienādojumam ir jābūt vismaz vienai reālai saknei, atšķirībā no kvadrātvienādojuma, kur abas saknes var būt iedomātas, ja diskriminants ir mazāks par nulli.

5. Vai kubiskā vienādojumam var būt vairāki risinājumi?

Jā, kubiskā vienādojumam var būt vairāki risinājumi, jo kubiskā vienādojumam var būt līdz pat trim atšķirīgām reālajām saknēm.

6. Ko jūs domājat ar vienādojuma pakāpi?

Maksimālo jaudu, kas vienādojumā ir mainīgajam, sauc par polinoma pakāpi.

7. Kāda ir atšķirība starp polinomu un vienādojumu?

Polinoms ir vienkārši algebrisks vienādojums, kurā mainīgā jauda ir nenegatīvs vesels skaitlis. Ja šo polinomu pielīdzina (=) ar skaitlisku vērtību vai citu polinomu, to sauc par vienādojumu.

8. Kas ir kubisko vienādojumu koeficientu teorēma?

Faktoru teorēma nosaka, ka, ja r ir kubiskā vienādojuma ax sakne (atrisinājums)³+ bx²+ cx + d = 0, tad x – r ir vienādojuma faktors.

9. Ko darīt, ja nevaru atrast precīzus risinājumus, izmantojot formulas?

Ja šķiet, ka nav iespējams atrast precīzus risinājumus, mēs varam izmantot skaitliskās metodes, piemēram, iteratīvās metodes (piemēram, Ņūtona metodi), lai tuvinātu vienādojuma saknes.

Uzziniet vairāk par Ņūtona Rafsona metode .