Loģistiskā regresija ir uzraudzīts mašīnmācīšanās algoritms izmanto klasifikācijas uzdevumi kur mērķis ir paredzēt varbūtību, ka gadījums pieder noteiktai klasei vai nē. Loģistiskā regresija ir statistisks algoritms, kas analizē attiecības starp diviem datu faktoriem. Rakstā ir apskatīti loģistikas regresijas pamati, veidi un ieviešanas veidi.
Satura rādītājs
- Kas ir loģistiskā regresija?
- Loģistikas funkcija – sigmoīda funkcija
- Loģistiskās regresijas veidi
- Loģistikas regresijas pieņēmumi
- Kā darbojas loģistikas regresija?
- Loģistikas regresijas koda ieviešana
- Precizitātes un atsaukšanas kompromiss loģistikas regresijas sliekšņa iestatījumos
- Kā novērtēt loģistikas regresijas modeli?
- Atšķirības starp lineāro un loģistisko regresiju
Kas ir loģistiskā regresija?
Loģistisko regresiju izmanto binārajam klasifikācija kur lietojam sigmoīdā funkcija , kas izmanto ievadi kā neatkarīgus mainīgos un rada varbūtības vērtību no 0 līdz 1.
Piemēram, mums ir divas klases: 0. klase un 1. klase, ja ievades loģistikas funkcijas vērtība ir lielāka par 0,5 (sliekšņa vērtība), tad tā pieder 1. klasei, pretējā gadījumā tā pieder 0. klasei. To sauc par regresiju, jo tā ir paplašinājums lineārā regresija bet galvenokārt tiek izmantots klasifikācijas problēmām.
Galvenie punkti:
- Loģistiskā regresija paredz kategoriski atkarīgā mainīgā izvadi. Tāpēc iznākumam ir jābūt kategoriskai vai diskrētai vērtībai.
- Tas var būt Jā vai Nē, 0 vai 1, patiess vai aplams utt., bet tā vietā, lai norādītu precīzu vērtību kā 0 un 1, tas dod varbūtības vērtības, kas atrodas no 0 līdz 1.
- Loģistiskajā regresijā tā vietā, lai pielāgotu regresijas līniju, mēs izmantojam S formas loģistikas funkciju, kas paredz divas maksimālās vērtības (0 vai 1).
Loģistikas funkcija – sigmoīda funkcija
- Sigmoīda funkcija ir matemātiska funkcija, ko izmanto, lai kartētu prognozētās vērtības ar varbūtībām.
- Tas attēlo jebkuru reālo vērtību citā vērtībā diapazonā no 0 līdz 1. Loģistiskās regresijas vērtībai ir jābūt no 0 līdz 1, kas nevar pārsniegt šo robežu, tāpēc tā veido līkni kā S forma.
- S formas līkni sauc par Sigmoid funkciju vai loģistikas funkciju.
- Loģistiskajā regresijā mēs izmantojam sliekšņa vērtības jēdzienu, kas definē 0 vai 1 varbūtību. Piemēram, vērtībām, kas pārsniedz sliekšņa vērtību, ir tendence uz 1, un vērtībai, kas ir zemāka par sliekšņa vērtībām, ir tendence uz 0.
Loģistiskās regresijas veidi
Pamatojoties uz kategorijām, loģistisko regresiju var iedalīt trīs veidos:
- Binomiāls: Binomiālajā loģistikas regresijā var būt tikai divi iespējamie atkarīgo mainīgo veidi, piemēram, 0 vai 1, Apstiprināts vai Neizdevies utt.
- Multinomiāls: Daudznomu loģistikas regresijā var būt 3 vai vairāki iespējami nesakārtoti atkarīgā mainīgā veidi, piemēram, kaķis, suņi vai aita
- Kārtējā: Kārtības loģistikas regresijā var būt 3 vai vairāki iespējami sakārtoti atkarīgo mainīgo veidi, piemēram, zems, vidējs vai augsts.
Loģistikas regresijas pieņēmumi
Mēs izpētīsim loģistikas regresijas pieņēmumus, jo šo pieņēmumu izpratne ir svarīga, lai nodrošinātu, ka mēs izmantojam atbilstošu modeļa pielietojumu. Pieņēmums ietver:
- Neatkarīgi novērojumi: katrs novērojums ir neatkarīgs no otra. tas nozīmē, ka starp ievades mainīgajiem nav korelācijas.
- Bināri atkarīgie mainīgie: tiek pieņemts, ka atkarīgajam mainīgajam jābūt bināram vai dihotomam, kas nozīmē, ka tam var būt tikai divas vērtības. Vairāk nekā divām kategorijām tiek izmantotas SoftMax funkcijas.
- Linearitātes sakarība starp neatkarīgiem mainīgajiem un logaritmiskām izredzēm. Attiecībai starp neatkarīgiem mainīgajiem un atkarīgā mainīgā logaritmi ir jābūt lineārai.
- Bez novirzēm: datu kopā nedrīkst būt novirzes.
- Liels izlases lielums: izlases lielums ir pietiekami liels
Loģistikas regresijā iesaistītās terminoloģijas
Šeit ir daži vispārīgi termini, kas saistīti ar loģistikas regresiju:
- Neatkarīgi mainīgie: Ievades raksturlielumi vai prognozēšanas faktori, kas tiek lietoti atkarīgā mainīgā prognozēm.
- Atkarīgais mainīgais: Mērķa mainīgais loģistikas regresijas modelī, ko mēs cenšamies prognozēt.
- Loģistikas funkcija: Formula, ko izmanto, lai attēlotu, kā neatkarīgie un atkarīgie mainīgie ir saistīti viens ar otru. Loģistikas funkcija pārveido ievades mainīgos par varbūtības vērtību no 0 līdz 1, kas atspoguļo iespējamību, ka atkarīgais mainīgais ir 1 vai 0.
- Izredzes: Tā ir attiecība tam, ka kaut kas notiek un kaut kas nenotiek. tā atšķiras no varbūtības, jo varbūtība ir attiecība, ka kaut kas notiks pret visu, kas varētu notikt.
- Log-izredzes: Log-izredzes, kas pazīstamas arī kā logit funkcija, ir koeficientu dabiskais logaritms. Loģistiskajā regresijā atkarīgā mainīgā logaritmiskās izredzes tiek modelētas kā neatkarīgo mainīgo un krustpunkta lineāra kombinācija.
- Koeficients: Loģistiskās regresijas modeļa aprēķinātie parametri parāda, kā neatkarīgie un atkarīgie mainīgie ir saistīti viens ar otru.
- Pārtvert: Konstants termins loģistikas regresijas modelī, kas atspoguļo logaritmus, kad visi neatkarīgie mainīgie ir vienādi ar nulli.
- Maksimālās varbūtības novērtējums : Loģistiskās regresijas modeļa koeficientu novērtēšanai izmantotā metode, kas maksimāli palielina modelī doto datu novērošanas iespējamību.
Kā darbojas loģistikas regresija?
Loģistiskās regresijas modelis pārveido lineārā regresija funkcija nepārtrauktas vērtības izvade kategoriskas vērtības izvadē, izmantojot sigmoīdu funkciju, kas attēlo jebkuru reālās vērtības neatkarīgo mainīgo kopu, kas tiek ievadīta vērtībā no 0 līdz 1. Šī funkcija ir pazīstama kā loģistikas funkcija.
Ļaujiet neatkarīgajām ievades funkcijām būt:
un atkarīgais mainīgais ir Y, kam ir tikai bināra vērtība, t.i., 0 vai 1.
pēc tam izmantojiet daudzlineāro funkciju ievades mainīgajiem X.
python konstruktors
Šeit
viss, ko mēs apspriedām iepriekš, ir lineārā regresija .
Sigmoīda funkcija
Tagad mēs izmantojam sigmoīdā funkcija kur ievade būs z un mēs atrodam varbūtību starp 0 un 1. t.i., paredzamo y.
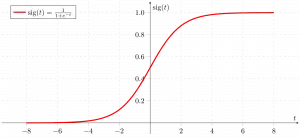
Sigmoīda funkcija
Kā parādīts iepriekš, figūras sigmoīda funkcija pārvērš nepārtrauktos mainīgos datus par varbūtība t.i., no 0 līdz 1.
sigma(z) tiecas uz 1 asz ightarrowinfty sigma(z) tiecas uz 0 asz ightarrow-infty sigma(z) vienmēr ir robežās no 0 līdz 1
kur varbūtību būt par klasi var izmērīt šādi:
Loģistikas regresijas vienādojums
Nepāra ir attiecība, ka kaut kas notiek un kaut kas nenotiek. tā atšķiras no varbūtības, jo varbūtība ir attiecība, ka kaut kas notiks pret visu, kas varētu notikt. tik dīvaini būs:
Dabiskā baļķa uzlikšana uz nepāra. tad log nepāra būs:
kā uzzināt displeja izmēru
tad galīgais loģistikas regresijas vienādojums būs:
Loģistikas regresijas varbūtības funkcija
Paredzamās varbūtības būs:
- ja y=1 Paredzētās varbūtības būs: p(X;b,w) = p(x)
- ja y = 0 Paredzētās varbūtības būs: 1-p(X;b,w) = 1-p(x)
Dabisko baļķu ņemšana no abām pusēm
Log-likelihood funkcijas gradients
Lai atrastu maksimālās iespējamības aplēses, mēs atšķiram w.r.t w,
Loģistikas regresijas koda ieviešana
Binomiālā loģistiskā regresija:
Mērķa mainīgajam var būt tikai 2 iespējamie veidi: 0 vai 1, kas var apzīmēt uzvaru pret zaudējumu, piespēli vai neveiksmi, miris vs dzīvs utt., šajā gadījumā tiek izmantotas sigmoīdas funkcijas, kas jau tika apspriestas iepriekš.
Nepieciešamo bibliotēku importēšana, pamatojoties uz modeļa prasībām. Šis Python kods parāda, kā izmantot krūts vēža datu kopu, lai ieviestu klasifikācijas loģistikas regresijas modeli.
Python3 # import the necessary libraries from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # load the breast cancer dataset X, y = load_breast_cancer(return_X_y=True) # split the train and test dataset X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23) # LogisticRegression clf = LogisticRegression(random_state=0) clf.fit(X_train, y_train) # Prediction y_pred = clf.predict(X_test) acc = accuracy_score(y_test, y_pred) print('Logistic Regression model accuracy (in %):', acc*100)> Izvade :
Loģistiskās regresijas modeļa precizitāte (%): 95.6140350877193
Daudznomu loģistikas regresija:
Mērķa mainīgajam var būt 3 vai vairāki iespējamie veidi, kas nav sakārtoti (t.i., veidiem nav kvantitatīvās nozīmes), piemēram, slimība A pret slimību B pret slimību C.
Šajā gadījumā sigmoidālās funkcijas vietā tiek izmantota softmax funkcija. Softmax funkcija K klasēm būs:
Šeit, K apzīmē elementu skaitu vektorā z, un i, j atkārtojas pār visiem vektora elementiem.
Tad c klases varbūtība būs:
Multinomiālajā loģistikas regresijā izvades mainīgajam var būt vairāk nekā divas iespējamās diskrētās izejas . Apsveriet ciparu datu kopu.
Python3 from sklearn.model_selection import train_test_split from sklearn import datasets, linear_model, metrics # load the digit dataset digits = datasets.load_digits() # defining feature matrix(X) and response vector(y) X = digits.data y = digits.target # splitting X and y into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1) # create logistic regression object reg = linear_model.LogisticRegression() # train the model using the training sets reg.fit(X_train, y_train) # making predictions on the testing set y_pred = reg.predict(X_test) # comparing actual response values (y_test) # with predicted response values (y_pred) print('Logistic Regression model accuracy(in %):', metrics.accuracy_score(y_test, y_pred)*100)> Izvade:
Loģistiskās regresijas modeļa precizitāte (%): 96.52294853963839
Kā novērtēt loģistikas regresijas modeli?
Mēs varam novērtēt loģistikas regresijas modeli, izmantojot šādus rādītājus:
- Precizitāte: Precizitāte nodrošina pareizi klasificētu gadījumu īpatsvaru.
Accuracy = frac{True , Positives + True , Negatives}{Total}
- Precizitāte: Precizitāte koncentrējas uz pozitīvo prognožu precizitāti.
Precision = frac{True , Positives }{True, Positives + False , Positives}
- Atsaukt (jutīgums vai patiesi pozitīvais rādītājs): Atsaukt mēra pareizi prognozēto pozitīvo gadījumu īpatsvaru starp visiem faktiskajiem pozitīvajiem gadījumiem.
Recall = frac{ True , Positives}{True, Positives + False , Negatives}
- F1 rezultāts: F1 rezultāts ir precizitātes un atsaukšanas harmoniskais vidējais.
F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}
- Apgabals zem uztvērēja darbības raksturlīknes (AUC-ROC): ROC līkne attēlo patieso pozitīvo rādītāju pret viltus pozitīvo likmi pie dažādiem sliekšņiem. AUC-ROC mēra laukumu zem šīs līknes, nodrošinot kopējo modeļa veiktspējas mērījumu dažādos klasifikācijas sliekšņos.
- Apgabals zem precizitātes-atsauces līknes (AUC-PR): Līdzīgi kā AUC-ROC, AUC-PR mēra laukumu zem precizitātes-atgādināšanas līknes, sniedzot kopsavilkumu par modeļa veiktspēju dažādos precīzās atsaukšanas kompromisos.
Precizitātes un atsaukšanas kompromiss loģistikas regresijas sliekšņa iestatījumos
Loģistiskā regresija kļūst par klasifikācijas paņēmienu tikai tad, kad tiek ņemts vērā lēmuma slieksnis. Sliekšņa vērtības iestatīšana ir ļoti svarīgs loģistikas regresijas aspekts un ir atkarīga no pašas klasifikācijas problēmas.
Lēmumu par sliekšņa vērtību lielā mērā ietekmē vērtības precizitāte un atcerēšanās. Ideālā gadījumā mēs vēlamies gan precizitāti, gan atgādinājumu, kas ir 1, taču tas notiek reti.
Gadījumā, ja a Precizitātes un atsaukšanas kompromiss , mēs izmantojam šādus argumentus, lai izlemtu par slieksni:
- Zema precizitāte/augsta atsaukšana: Lietojumprogrammās, kurās vēlamies samazināt viltus negatīvo atzīmju skaitu, vienlaikus nesamazinot viltus pozitīvo atzīmju skaitu, mēs izvēlamies lēmuma vērtību, kurai ir zema precizitātes vērtība vai augsta atsaukšanas vērtība. Piemēram, vēža diagnostikas lietojumprogrammā mēs nevēlamies, lai kāds slims pacients tiktu klasificēts kā neskarts, nepievēršot īpašu uzmanību, ja pacientam tiek nepareizi diagnosticēts vēzis. Tas ir tāpēc, ka vēža neesamību var noteikt ar turpmākām medicīniskām slimībām, bet slimības klātbūtni nevar noteikt jau noraidītam kandidātam.
- Augsta precizitāte/zema atsaukšana: Lietojumprogrammās, kurās vēlamies samazināt viltus pozitīvo atzīmju skaitu, nesamazinot viltus negatīvo atzīmju skaitu, mēs izvēlamies lēmuma vērtību, kurai ir augsta precizitātes vērtība vai zema Recall vērtība. Piemēram, ja mēs klasificējam klientus, vai viņi uz personalizētu sludinājumu reaģēs pozitīvi vai negatīvi, mēs vēlamies būt pilnīgi pārliecināti, ka klients uz reklāmu reaģēs pozitīvi, jo pretējā gadījumā negatīva reakcija var izraisīt potenciālo pārdošanas apjomu zudumu no klientu.
Atšķirības starp lineāro un loģistisko regresiju
Atšķirība starp lineāro regresiju un loģistisko regresiju ir tāda, ka lineārās regresijas izvade ir nepārtraukta vērtība, kas var būt jebkas, savukārt loģistiskā regresija paredz varbūtību, ka gadījums pieder noteiktai klasei vai nē.
Lineārā regresija | Loģistiskā regresija |
|---|---|
Lineāro regresiju izmanto, lai prognozētu nepārtrauktu atkarīgo mainīgo, izmantojot noteiktu neatkarīgu mainīgo kopu. | Loģistisko regresiju izmanto, lai prognozētu kategoriski atkarīgo mainīgo, izmantojot noteiktu neatkarīgu mainīgo kopu. |
Regresijas problēmas risināšanai izmanto lineāro regresiju. | To izmanto klasifikācijas problēmu risināšanai. |
Tajā mēs prognozējam nepārtraukto mainīgo vērtību | Tajā mēs prognozējam kategorisko mainīgo vērtības |
Šajā mēs atrodam vispiemērotāko līniju. | Šajā mēs atrodam S-līkni. |
Precizitātes noteikšanai tiek izmantota mazākā kvadrāta novērtējuma metode. | Precizitātes novērtēšanai tiek izmantota maksimālās varbūtības aplēses metode. |
Izvadei jābūt nepārtrauktai vērtībai, piemēram, cenai, vecumam utt. | Izvadei ir jābūt kategoriskai vērtībai, piemēram, 0 vai 1, Jā vai nē utt. |
Tam bija nepieciešama lineāra sakarība starp atkarīgajiem un neatkarīgajiem mainīgajiem. lineārā meklēšana java | Tas neprasa lineāras attiecības. |
Starp neatkarīgiem mainīgajiem var būt kolinearitāte. | Starp neatkarīgiem mainīgajiem nevajadzētu būt kolinearitātei. |
Loģistiskā regresija — bieži uzdotie jautājumi (FAQ)
Kas ir loģistikas regresija mašīnmācībā?
Loģistiskā regresija ir statistikas metode mašīnmācīšanās modeļu izstrādei ar bināri atkarīgiem mainīgajiem, t.i., binārajiem. Loģistiskā regresija ir statistikas metode, ko izmanto, lai aprakstītu datus un attiecības starp vienu atkarīgo mainīgo un vienu vai vairākiem neatkarīgiem mainīgajiem.
Kādi ir trīs loģistikas regresijas veidi?
Loģistisko regresiju iedala trīs veidos: binārā, daudznomu un kārtas. Tie atšķiras gan izpildījumā, gan teorijā. Binārā regresija ir saistīta ar diviem iespējamiem rezultātiem: jā vai nē. Multinomu loģistikas regresija tiek izmantota, ja ir trīs vai vairāk vērtības.
Kāpēc klasifikācijas problēmai tiek izmantota loģistikas regresija?
Loģistisko regresiju ir vieglāk īstenot, interpretēt un apmācīt. Tas ļoti ātri klasificē nezināmus ierakstus. Ja datu kopa ir lineāri atdalāma, tā darbojas labi. Modeļa koeficientus var interpretēt kā pazīmju nozīmīguma rādītājus.
Kas atšķir loģistisko regresiju no lineārās regresijas?
Kamēr lineāro regresiju izmanto, lai prognozētu nepārtrauktus rezultātus, loģistikas regresiju izmanto, lai prognozētu iespējamību, ka novērojums ietilpst noteiktā kategorijā. Loģistiskā regresija izmanto S formas loģistikas funkciju, lai kartētu prognozētās vērtības no 0 līdz 1.
Kādu lomu loģistikas funkcija spēlē loģistikas regresijā?
Loģistiskā regresija balstās uz loģistikas funkciju, lai pārvērstu produkciju par varbūtības rādītāju. Šis rādītājs atspoguļo varbūtību, ka novērojums pieder noteiktai klasei. S formas līkne palīdz noteikt slieksni un klasificēt datus bināros rezultātos.
