Termiņš Memoizācija nāk no latīņu vārda memorandu ( atcerēties ), kas amerikāņu angļu valodā parasti tiek saīsināts uz memo un kas nozīmē pārveidot funkcijas rezultātus par kaut ko tādu, kas jāatceras.
Skaitļošanā memoizāciju izmanto, lai paātrinātu datorprogrammas, novēršot atkārtotu rezultātu aprēķināšanu un izvairoties no atkārtotiem izsaukumiem funkcijām, kas apstrādā vienu un to pašu ievadi.

Kas ir memoizācija
Satura rādītājs
- Kas ir memoizācija?
- Kāpēc tiek izmantota memoization>
- Kur izmantot Memoization?
- Memoizācijas veidi
- Kā memoizācijas paņēmiens tiek izmantots dinamiskajā programmēšanā?
- Kā iegaumēšana atšķiras no tabulēšanas?
- Kodēšanas prakses problēmas iegaumēšanai
- FAQ
- 1) Vai memoizācija ir labāka par DP?
- 2) Vai iegaumēšana ir tas pats, kas kešatmiņa?
- 3) Kāpēc iegaumēšana notiek no augšas uz leju?
- 4) Vai memoizācija izmanto rekursiju?
- 5) Vai man vajadzētu izmantot tabulēšanu vai iegaumēšanu?
- 6) Kur tiek izmantota iegaumēšana?
- 7) Kāpēc to sauc par memoizāciju?
- 8) Kā iegaumēšana samazina laika sarežģītību?
- 9) Kāda ir atšķirība starp iegaumēšanu un kešatmiņu?
- 10) Kāpēc tabulēšana ir ātrāka nekā iegaumēšana?
- Secinājums
Kāpēc tiek izmantota atmiņa?
Memoizācija ir īpaša forma kešatmiņa kas tiek izmantots dinamiskā programmēšana . Kešatmiņas saglabāšanas mērķis ir uzlabot mūsu programmu veiktspēju un nodrošināt datu pieejamību, ko var izmantot vēlāk. Tas pamatā saglabā iepriekš aprēķināto apakšproblēmas rezultātu un izmanto saglabāto rezultātu tai pašai apakšproblēmai. Tas noņem papildu pūles, lai atkal un atkal aprēķinātu vienu un to pašu problēmu. Un mēs jau zinām, ka, ja viena un tā pati problēma atkārtojas atkal un atkal, tad šai problēmai ir rekursīvs raksturs.
Kur izmantot Memoization?
Mēs varam izmantot memoizācijas paņēmienu, ja iepriekš aprēķināto rezultātu izmantošana nonāk attēlā. Šāda veida problēma galvenokārt tiek izmantota saistībā ar rekursija , īpaši ar problēmām, kas saistītas apakšproblēmas, kas pārklājas .
Ņemsim piemēru, kur viena un tā pati apakšproblēma atkārtojas atkal un atkal.
Piemērs, lai parādītu, kur izmantot iegaumēšanu:
Let us try to find the factorial of a number .>
Zemāk ir a rekursīvā metode lai atrastu skaitļa faktoriālu:
int faktoriāls (neparakstīts int n)
{
ja (n == 0)
atgriešanās 1;
return n * faktoriāls(n – 1);
}
Kas notiks, ja izmantosim šo rekursīvo metodi?
Ja ierakstīsit visu iepriekš minētā fragmenta kodu, pamanīsit, ka kodā būs 2 metodes:
1. factorial(n) 2. main()>
Ja mums ir vairāki vaicājumi, lai atrastu faktoriālu, piemēram, lai atrastu faktoriālu 2, 3, 9 un 5, tad mums būs jāizsauc faktoriāls () metode 4 reizes:
factorial(2) factorial(3) factorial(9) factorial(5)>
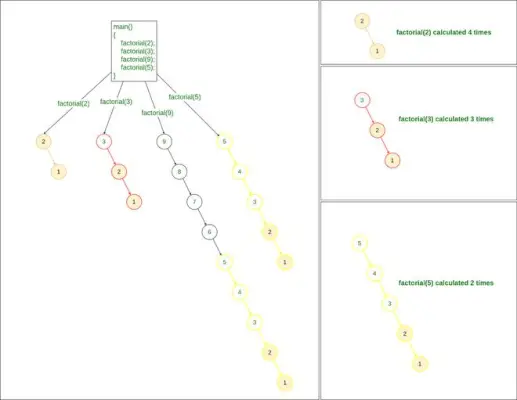
Rekursīvā metode faktoriāla atrašanai
Tāpēc var droši teikt, ka skaitļu K skaitļu faktoriāla atrašanai būs nepieciešama laika sarežģītība O(N*K)
- O(N) lai atrastu konkrēta skaitļa faktoriālu, un
- bultiņa) lai izsauktu faktoriālo() metodi K dažādos laikos.
Kā Memoization var palīdzēt ar šādām problēmām?
Ja mēs novērojam iepriekšminēto problēmu, aprēķinot koeficientu 9:
Alise Manjonoka
- Mēs aprēķinām koeficientu 2
- Mēs arī aprēķinām faktoriālu no 3,
- un Mēs aprēķinām arī 5 faktoriālu
Tāpēc, ja mēs saglabājam katra atsevišķa faktoriāla rezultātu pirmajā aprēķina reizē, mēs varam viegli atgriezt jebkura vajadzīgā skaitļa faktoriālu tikai O(1) laikā. Šis process ir pazīstams kā Memoizācija .
Risinājums, izmantojot Memoization (kā darbojas memoization?):
Ja mēs vispirms atrodam koeficientu 9 un saglabājam atsevišķu apakšproblēmu rezultātus, mēs varam viegli izdrukāt katras ievades faktoriālu O(1).
Tāpēc laika sarežģītība faktoriālo skaitļu atrašanai, izmantojot iegaumēšanu, būs O(N)
- O(N) lai atrastu lielākās ievades koeficientu
- O(1) lai izdrukātu katras ievades faktoriālu.
Memoizācijas veidi
Memoizācijas ieviešana ir atkarīga no mainīgajiem parametriem, kas ir atbildīgi par problēmas risināšanu. Ir dažādas kešatmiņas dimensijas, kas tiek izmantotas memoizācijas tehnikā. Tālāk ir norādīti daži no tiem:
- 1D iegaumēšana: Rekursīvā funkcija, kurai ir tikai viens arguments, kura vērtība nebija nemainīga pēc katras funkcijas izsaukšanas.
- 2D iegaumēšana: Rekursīva funkcija, kurai ir tikai divi argumenti, kuru vērtība nebija nemainīga pēc katras funkcijas izsaukuma.
- 3D memoization : rekursīva funkcija, kurai ir tikai trīs argumenti, kuru vērtības nebija nemainīgas pēc katras funkcijas izsaukšanas.
Kā Memoization tehnika tiek izmantota dinamiskajā programmēšanā?
Dinamiskā programmēšana palīdz efektīvi atrisināt problēmas, kurām ir pārklājošas apakšproblēmas un optimālas apakšstruktūras īpašības. Dinamiskās programmēšanas ideja ir sadalīt problēmu mazākās apakšproblēmās un saglabāt rezultātu turpmākai lietošanai, tādējādi novēršot nepieciešamību atkārtoti aprēķināt rezultātu.
Ir divas pieejas, lai formulētu dinamisku programmēšanas risinājumu:
- No augšas uz leju pieeja: Šī pieeja seko iegaumēšana tehnika . Tas sastāv no rekursija un kešatmiņa . Aprēķinos rekursija apzīmē funkciju atkārtotas izsaukšanas procesu, savukārt kešatmiņa attiecas uz starprezultātu glabāšanas procesu.
- Augšupēja pieeja: Šī pieeja izmanto tabulēšana tehnika ieviest dinamiskās programmēšanas risinājumu. Tas risina tās pašas problēmas kā iepriekš, bet bez atkārtošanās. Šajā pieejā iterācija aizstāj rekursiju. Līdz ar to nav steka pārpildes kļūdu vai rekursīvo procedūru papildu izmaksu.
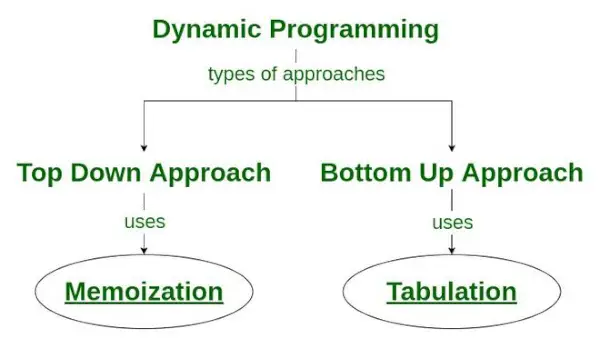
Kā Memoization tehnika tiek izmantota dinamiskajā programmēšanā
Kā iegaumēšana atšķiras no tabulēšanas?

Tabulēšana pret memoizāciju
Lai iegūtu sīkāku informāciju, lūdzu, skatiet: Tabulēšana pret memoizāciju
Kodēšanas prakses problēmas memoizācijā
| Jautājums | Raksts | Prakse | Video |
|---|---|---|---|
| Saskaitiet veidus, kā sasniegt n-tās kāpnes | Skatīt | Atrisināt | Skatīties |
| Vārdu pārtraukuma problēma | DP-32 | Skatīt | Atrisināt | Skatīties |
| Programma Fibonači skaitļiem | Skatīt | Atrisināt | Skatīties |
| n-tais katalāņu numurs | Skatīt | Atrisināt | Skatīties |
| Zelta raktuves problēma | Skatīt | Atrisināt | Skatīties |
| Apakškopas summas problēma | Skatīt | Atrisināt | Skatīties |
| Stieņa griešana | Skatīt | Atrisināt | Skatīties |
| Minimālo izmaksu ceļš | Skatīt | Atrisināt | Skatīties |
| Minimālais lēcienu skaits, lai sasniegtu beigas | Skatīt | Atrisināt | Skatīties |
| Garākā palindromiskā apakšvirkne | 1. komplekts | Skatīt | Atrisināt | Skatīties |
| Garākā atkārtotā secība | Skatīt | Atrisināt | Skatīties |
| Saskaitiet veidus, kā sasniegt n-tās kāpnes, izmantojot 1., 2. vai 3. darbību | Skatīt | Atrisināt | Skatīties |
| Saskaitiet dažādus veidus, kā izteikt N kā 1, 3 un 4 summu | Skatīt | Atrisināt | Skatīties |
| Saskaitiet veidus, kā pārvarēt attālumu | Skatīt | Atrisināt | Skatīties |
| To masīvu skaits, kuriem ir secīgs elements ar dažādām vērtībām | Skatīt | Atrisināt | Skatīties |
| Lielākā summa blakus esošais apakšgrupa | Skatīt | Atrisināt | Skatīties |
| Mazākā summa blakus esošais apakšgrupa | Skatīt | Atrisināt | Skatīties |
| Unikāli ceļi režģī ar šķēršļiem | Skatīt | Atrisināt | Skatīties |
| Dažādi veidi, kā summēt n, izmantojot skaitļus, kas ir lielāki vai vienādi ar m | Skatīt | Atrisināt | Skatīties |
Bieži uzdotie jautājumi (FAQ) par Memoization
1: Vai memoizācija ir labāka par DP?
Memoizācija ir lejupejoša pieeja problēmas risināšanai ar dinamisku programmēšanu. To sauc par memoizāciju, jo mēs izveidosim piezīmi vērtībām, kas atgrieztas, risinot katru problēmu.
2. Vai iegaumēšana ir tas pats, kas saglabāšana kešatmiņā?
Memoization faktiski ir īpašs kešatmiņas veids. Termins kešatmiņa parasti var attiekties uz jebkuru uzglabāšanas paņēmienu (piemēram, HTTP kešatmiņu) turpmākai lietošanai, bet iegaumēšana konkrētāk attiecas uz kešatmiņas funkciju, kas atgriež vērtību.
3. Kāpēc iegaumēšana notiek no augšas uz leju?
No augšas uz leju pieeja lielā problēma sadala vairākās apakšproblēmās. ja apakšproblēma jau ir atrisināta, izmantojiet atbildi atkārtoti. Pretējā gadījumā atrisiniet apakšproblēmu un saglabājiet rezultātu atmiņā.
4: vai memoizācijā tiek izmantota rekursija?
Memoizācija problēmas risināšanai tiek izmantota no augšas uz leju. Tas sastāv no rekursijas un kešatmiņas. Aprēķinos rekursija apzīmē funkciju atkārtotas izsaukšanas procesu, savukārt kešatmiņa attiecas uz starprezultātu glabāšanas procesu.
5. Vai man vajadzētu izmantot tabulēšanu vai iegaumēšanu?
Problēmām, kurām ir jāatrisina visas apakšproblēmas, tabulēšana parasti pārspēj iegaumēšanu ar nemainīgu koeficientu. Tas ir tāpēc, ka tabulēšanai nav rekursijas, kas samazina laiku, kas nepieciešams rekursijas izsaukuma steka atrisināšanai no steka atmiņas.
Ikreiz, kad ir jāatrisina kāda apakšproblēma, lai atrisinātu sākotnējo problēmu, priekšroka dodama iegaumēšanai, jo apakšproblēma tiek atrisināta laiski, t.i., tiek veikti tikai nepieciešamie aprēķini.
6: Kur tiek izmantota iegaumēšana?
Memoizācija ir optimizācijas paņēmiens, ko izmanto, lai paātrinātu datorprogrammu darbību, saglabājot kešatmiņā dārgu funkciju izsaukumu rezultātus un atgriežot tos, kad atkal tiek sastaptas tās pašas ievades.
7: Kāpēc to sauc par iegaumēšanu?
Termins “atgādināšana” nāk no latīņu vārda memorandum (atcerēties), kas amerikāņu angļu valodā parasti tiek saīsināts uz memorandu un kas nozīmē pārveidot funkcijas rezultātus par kaut ko, kas jāatceras.
8: Kā iegaumēšana samazina laika sarežģītību?
Vienas un tās pašas problēmas risināšana atkal un atkal prasa laiku un palielina visas programmas izpildes laika sarežģītību. Šo problēmu var atrisināt, saglabājot kešatmiņu vai atmiņu, kurā mēs saglabāsim jau aprēķināto problēmas rezultātu kādai konkrētai ievadei. Tātad, ja mēs nevēlamies pārrēķināt to pašu problēmu, mēs varam vienkārši izmantot atmiņā saglabāto rezultātu un samazināt laika sarežģītību.
9: Kāda ir atšķirība starp iegaumēšanu un kešatmiņu?
Atgādināšana faktiski ir īpašs kešatmiņas veids, kas ietver funkcijas atgriešanas vērtības saglabāšanu kešatmiņā, pamatojoties uz ievadi. Kešatmiņa ir vispārīgāks termins. Piemēram, HTTP kešatmiņa ir kešatmiņa, bet tā nav iegaumēšana.
10: Kāpēc tabulēšana ir ātrāka nekā iegaumēšana?
Tabulēšana parasti ir ātrāka nekā iegaumēšana, jo tā ir iteratīva un apakšproblēmu risināšanai nav nepieciešami rekursīvie izsaukumi.
Memoizācija ir paņēmiens, ko izmanto datorzinātnēs, lai paātrinātu rekursīvu vai skaitļošanas ziņā dārgu funkciju izpildi, saglabājot funkciju izsaukumu rezultātus kešatmiņā un atgriežot kešatmiņā saglabātos rezultātus, kad tās pašas ievades atkārtojas.
Memoizācijas pamatideja ir saglabāt funkcijas izvadi noteiktai ievades kopai un atgriezt kešatmiņā saglabāto rezultātu, ja funkcija tiek izsaukta vēlreiz ar tām pašām ieejām. Šis paņēmiens var ietaupīt aprēķina laiku, jo īpaši funkcijām, kuras tiek izsauktas bieži vai kurām ir liela laika sarežģītība.
Tālāk ir sniegts detalizēts ceļvedis iegaumēšanas ieviešanai.
Nosakiet funkciju, kuru vēlaties optimizēt, izmantojot memoizāciju. Šai funkcijai vajadzētu būt atkārtotiem un dārgiem aprēķiniem vienai un tai pašai ievadei.
Izveidojiet vārdnīcas objektu, lai saglabātu funkcijas kešatmiņā saglabātos rezultātus. Vārdnīcas taustiņiem ir jābūt funkcijas ievades parametriem, un vērtībām jābūt aprēķinātajiem rezultātiem.
Funkcijas sākumā pārbaudiet, vai ievades parametri jau ir kešatmiņas vārdnīcā. Ja tie ir, atgrieziet kešatmiņā saglabāto rezultātu.
Ja ievades parametri nav kešatmiņas vārdnīcā, aprēķiniet rezultātu un saglabājiet to kešatmiņas vārdnīcā ar ievades parametriem kā atslēgu.
Atgrieziet aprēķināto rezultātu.
Šeit ir Python koda piemērs iegaumēšanas ieviešanai, izmantojot vārdnīcu:
Python3
def> fibonacci(n, cache>=>{}):> >if> n>in> cache:> >return> cache[n]> >if> n>=>=> 0>:> >result>=> 0> >elif> n>=>=> 1>:> >result>=> 1> >else>:> >result>=> fibonacci(n>->1>)>+> fibonacci(n>->2>)> >cache[n]>=> result> >return> result> |
>
normālas formas
>Izvade
>
Iepriekš minētajā kodā mēs definējam funkciju, ko sauc par fibonači, kas aprēķina n-to skaitli Fibonači secībā. Mēs izmantojam vārdnīcas objektu, ko sauc par kešatmiņu, lai saglabātu funkciju izsaukumu rezultātus. Ja ievades parametrs n jau ir kešatmiņas vārdnīcā, mēs atgriežam kešatmiņā saglabāto rezultātu. Pretējā gadījumā mēs aprēķinām rezultātu, izmantojot rekursīvus fibonači funkcijas izsaukumus, un pirms atgriešanas saglabājam to kešatmiņas vārdnīcā.
Memoizāciju var izmantot, lai optimizētu daudzu funkciju veiktspēju, kurām ir atkārtoti un dārgi aprēķini. Saglabājot funkciju izsaukumu rezultātus kešatmiņā, mēs varam izvairīties no nevajadzīgiem aprēķiniem un paātrināt funkcijas izpildi.
Secinājums
Memoization ir programmēšanas koncepcija, un to var izmantot jebkurā programmēšanas valodā. Tās absolūtais mērķis ir optimizēt programmu. Parasti šī problēma tiek novērota, kad programmas veic smagus aprēķinus. Šis paņēmiens saglabā kešatmiņu visu iepriekšējo rezultātu, kas tiek aprēķināts, lai tas nebūtu jāpārrēķina tās pašas problēmas gadījumā.
Saistītie raksti:
- Memoizācija, izmantojot dekoratorus programmā Python
- JavaScript Memoization
