Daudzstūris matemātikā ir divdimensiju forma, kas sastāv no taisnām līnijām, kas veido slēgtu daudzstūra ķēdi. Vārds daudzstūris cēlies no vārdiem poly un gon, kas nozīmē daudz un malas.
Daudzstūri var būt vienkārši vai paši krustojas. Vienkāršs daudzstūris pats nekrustojas, izņemot secīgu segmentu kopīgos galapunktus. Daudzstūra ķēde, kas šķērso pati sevi, rada paškrustojošu daudzstūri. Daudzstūrus var klasificēt arī kā ieliektus vai izliektus.
Šajā rakstā mēs esam detalizēti minējuši daudzstūrus un to veidus, formulas un piemērus.
| Svarīgi fakti par daudzstūriem | |
|---|---|
| Daudzstūra iekšējo leņķu summa | (n–2) × 180° |
| Diagonāļu skaits daudzstūrī | n(n–3)/2 |
| Regulāra daudzstūra iekšējais leņķis | {(n–2) × 180°}/n |
| Regulāra daudzstūra ārējais leņķis | 360°/n |
Satura rādītājs
- Kas ir daudzstūri?
- Daudzstūra diagramma, kuras pamatā ir malu skaits
- Daudzstūru īpašības
- Daudzstūru formas
- Daudzstūru veidi
- Daudzstūru formulas
- Leņķi daudzstūros
- FAQ
Kas ir daudzstūri?
Termins “daudzstūris” ir cēlies no grieķu vārda polugonos, kur “poli” apzīmē “daudz”, bet “gon” apzīmē “leņķi”. Parasti daudzstūris ir slēgta figūra, ko veido taisnas līnijas, kuru iekšējie leņķi veido tie līnijas. Lai izveidotu slēgtu formu, ir nepieciešami vismaz trīs līniju segmenti. To parasti sauc par trīsstūri vai trīsstūri. Vispārīgais termins n-šķautņu daudzstūrim ir n-stūris.
Daudzstūra definīcija
Daudzstūri ir plakanas, divdimensiju figūras, kas sastāv no taisnām malām, kas veido pilnībā noslēgtu formu. Ģeometrijā daudzstūris ir plakana figūra, kas sastāv no līniju segmentiem, kas savienoti, veidojot slēgtu daudzstūra ķēdi. Tie sastāv no taisnām malām, nevis izliekumiem, un tiem var būt dažāds malu skaits. Daži dažāda veida daudzstūri ir: atvērti, tikai robežojas, slēgti un paši krustojas.
Ģeometrijā daudzstūris tiek definēts kā slēgta, divdimensiju forma, kas atrodas plaknē un ir norobežota ar taisnām malām.
Daudzstūrim nav izliektu malu, un tā malas ir taisni segmenti, kas nosaka tā robežu. Šo malu satikšanās punktus sauc par virsotnēm vai stūriem.
Daudzstūru piemēri
Matemātikas ziņā daudzstūru piemēri ir trijstūri, sešstūri, piecstūri un četrstūri. Daudzstūra reāli piemēri ir taisnstūra formas ekrāns jūsu klēpjdatorā, televizorā, mobilajā tālrunī; taisnstūrveida futbola laukums vai rotaļu laukums, Bermudu trijstūris un Ēģiptes trīsstūra formas piramīdas.

Daudzstūra daļas
Daudzstūris sastāv no trim pamata sastāvdaļām:
- Daudzstūra malas: Daudzstūru malas ir daudzstūru robežas, kas nosaka slēgto apgabalu.
- Virsotnes: Punktu, kurā saskaras divas puses, sauc par virsotni.
- Leņķi: Daudzstūris satur gan iekšējos, gan ārējos leņķus. Iekšējais leņķis veidojas daudzstūra slēgtajā apgabalā, krustojoties tā malām.
Daudzstūra diagramma, kuras pamatā ir malu skaits
Daudzstūra nomenklatūra, kas definēta, pamatojoties uz to malu skaitu. Tas ir apzīmēts kā n-gons, kur “n” apzīmē malu skaitu. Daudzstūri parasti tiek identificēti pēc to malu daudzuma. Piemēram, daudzstūris ar piecām malām tiek saukts par 5 stūru, savukārt viens ar desmit stūriem tiek saukts par 10 stūriem.
| Daudzstūru diagramma | ||||
|---|---|---|---|---|
| Daudzstūru formu nosaukumi | Sānu skaits | Virsotņu skaits | Diagonāļu skaits | Iekšējā leņķa mērs regulārai formai |
| Trīsstūris vaicājuma atlasītājs | Daudzstūri ar 3 malām | 3 | 0 | 60° |
| Četrstūris | Daudzstūri ar 4 malām | 4 | 2 | 90° |
| Pentagons | Daudzstūri ar 5 malām | 5 | 5 | 108° |
| Sešstūris | Daudzstūri ar 6 malām | 6 | 9 | 120° |
| Septiņstūris | Daudzstūri ar 7 malām | 7 | 14 | 128,571° |
| Astoņstūris | Daudzstūri ar 8 malām | 8 | divdesmit | 135° |
| Nonagon | Daudzstūri ar 9 malām | 9 | 27 | 140° |
| Decagon | Daudzstūri ar 10 malām | 10 | 35 | 144° |
| Hendecagon | Daudzstūri ar 11 malām | vienpadsmit | 44 | 147,273° |
| Dodecagon | Daudzstūri ar 12 malām | 12 | 54 | 150° |
Daudzstūru īpašības
Daudzstūru īpašības tos viegli identificē. Šādas īpašības palīdz viegli uzzināt daudzstūrus:
- Daudzstūris ir slēgta forma, kurai nav atvērtu galu. Izcelsmei un beigu punktam jābūt vienādam.
- Tam ir plakana forma, kas sastāv no līniju segmentiem vai taisnām līnijām, kas kopā veido figūru.
- Kā divdimensiju vienība daudzstūris pastāv tikai garuma un platuma dimensijās, un tam trūkst dziļuma vai augstuma.
- Tam ir trīs vai vairākas malas, lai izveidotu daudzstūri.
- Daudzstūra leņķi var atšķirties. Tas parāda atšķirīgu konfigurāciju.
- Daudzstūra malu garums var atšķirties; tas var būt un var nebūt vienāds visā daudzstūrī.
Daudzstūru formas
Daudzstūris ir plakana, divdimensiju forma, ko raksturo taisnas malas, kas savienotas, veidojot slēgtu figūru. Daudzstūra formu piemēri:
- Trīsstūris
- Četrstūris
- Pentagons
- Sešstūris
- Septiņstūris
- Astoņstūris
- Nonagon
- Desmitstūris
Trīsstūris
- Tam ir 3 malas un 3 virsotnes.
- Tam nav diagonāļu.
- Interjera summa ir 180°.
Četrstūris
- Tam ir 4 malas un 4 virsotnes.
- Tam ir 2 diagonāles.
- Iekšējā leņķa summa ir 360°.
Pentagons
- Tam ir 5 malas un 5 virsotnes.
- Tam ir 5 diagonāles.
- Iekšējā leņķa summa ir 540°.
Sešstūris
- Tam ir 6 malas un 6 virsotnes.
- Tam ir 9 diagonāles.
- Iekšējā leņķa summa ir 720°.
Septiņstūris
- Tam ir 7 malas un 7 virsotnes.
- Tam ir 14 diagonāles.
- Iekšējā leņķa summa ir 900°.
Astoņstūris
- Tam ir 8 malas un 8 virsotnes.
- Tam ir 20 diagonāles.
- Iekšējā leņķa summa ir 1080°.
Nonagon
- Tam ir 9 malas un 9 virsotnes.
- Tam ir 27 diagonāles.
- Iekšējā leņķa summa ir 1260°.
Decagon
- Tam ir 10 malas un 10 virsotnes.
- Tam ir 35 diagonāles.
- Iekšējā leņķa summa ir 1440°.
Daudzstūru veidi
Atkarībā no malām un leņķiem daudzstūrus var iedalīt dažādos veidos pēc dažādiem principiem, piemēram:
- Uz sānu pamata
- Pamatojoties uz leņķiem
- Pamatojoties uz robežām
Daudzstūri uz malu pamata
Daudzstūrus var iedalīt divos galvenajos veidos, pamatojoties uz to malu īpašībām:
- Regulārs daudzstūris
- Neregulārs daudzstūris
Regulārs daudzstūris
Regulārais daudzstūris atšķiras ar to, ka visām malām ir vienāds garums un visiem iekšējiem leņķiem ir vienādi izmēri. Tas var būt gan vienādmalu, gan vienādstūrveida. Regulāru daudzstūru piemēri ir trīsstūris, četrstūris, piecstūris un sešstūris.

Regulārs daudzstūris
Neregulārs daudzstūris
Neregulāram daudzstūrim ir nevienāda garuma malas un dažādu izmēru leņķi. Jebkurš daudzstūris, kas neatbilst regulāra daudzstūra kritērijiem, tiek klasificēts kā neregulārs. Bieži sastopami neregulāra daudzstūra piemēri ir skalēna trīsstūris, četrstūri, piemēram, taisnstūris, trapece vai pūķis, kā arī neregulāras piecstūra un sešstūra struktūras.
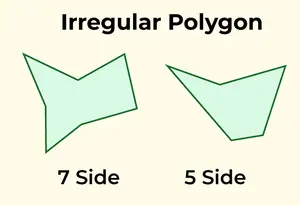
Neregulārs daudzstūris
Daudzstūri, pamatojoties uz leņķiem
Daudzstūrus var iedalīt divās galvenajās kategorijās, pamatojoties uz to leņķu raksturu:
- Izliekts daudzstūris
- Ieliekts daudzstūris
Izliekts daudzstūris
Izliektam daudzstūrim nav iekšējā leņķa, kas būtu lielāks par 180°. Izliektiem daudzstūriem var būt trīs vai vairākas malas. Izliektos daudzstūros visas diagonāles atrodas slēgtās figūras iekšpusē. Parasti izliektu daudzstūru piemēri ir trīsstūri, visi izliektie četrstūri, kā arī regulāri piecstūri un sešstūri
Ieliekts daudzstūris
Ieliektam daudzstūrim ir vismaz viens iekšējais leņķis, kas ir refleksa leņķis un ir vērsts uz iekšu. Ieliektiem daudzstūriem ir vismaz četras malas. Šāda veida daudzstūrim ir vismaz viens iekšējais leņķis, kas ir lielāks par 180°. Ieliektos daudzstūros dažas diagonāles sniedzas ārpus pievienotās figūras. Ieliektu daudzstūru piemēri ir šautriņas vai bultas uzgalis četrstūrī, kā arī noteikti neregulāri piecstūri un sešstūri.
Atšķirība starp ieliektiem un izliektiem daudzstūriem
Tālāk esošajā tabulā aplūkosim atšķirību starp izliekto un ieliekto daudzstūri:

| Izliekts daudzstūris | Ieliekts daudzstūris |
|---|---|
| Viss izliektas formas perimetrs stiepjas uz āru bez iekšējiem ievilkumiem. | Ieliektai formai ir vismaz viena uz iekšpusi vērsta daļa, kas norāda uz iespiedumu. |
| Izliektā daudzstūrī visi iekšējie leņķi ir zem 180°. | Ieliektā daudzstūrī ir vismaz viens iekšējais leņķis, kas pārsniedz 180°. |
| Jebkura līnija, kas savieno divas izliektas formas virsotnes, pilnībā atrodas formas robežās. | Līnija, kas savieno jebkuras divas ieliektas formas virsotnes, var krustot formas iekšpusi vai arī nē. |
Daudzstūri, pamatojoties uz robežām
Daudzstūrus var iedalīt divos galvenajos tipos, pamatojoties uz to robežu raksturu:
- Vienkāršs daudzstūris
- Sarežģīts daudzstūris
Vienkāršs daudzstūris
Vienkāršu daudzstūri raksturo vienskaitļa robeža, kas nekrustojas. Citiem vārdiem sakot, tas nešķērso sevi, un tas sastāv no vienas robežas.
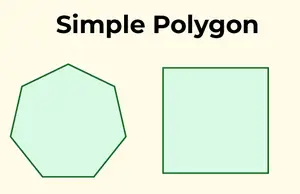
Vienkārši daudzstūri
Sarežģīts daudzstūris
No otras puses, komplekso daudzstūri nosaka pats krustojums. Tās struktūrā tas sastāv no vairāk nekā vienas robežas. Sarežģītos poligonos robeža krustojas, veidojot vairākus atšķirīgus apgabalus daudzstūrī.

Sarežģīts daudzstūris
Lasīt vairāk par Daudzstūru veidi.
Daudzstūru formulas
Ģeometrijā ir vairākas formulas, kas saistītas ar daudzstūriem. Daži no visbiežāk izmantotajiem ir:
- Apgabala formula
- Perimetra formula
- Diagonāļu skaits
Visas formulas, kas saistītas ar dažādiem daudzstūriem, ir apskatītas zemāk:
Daudzstūru apgabals
Daudzstūra laukums attēlo kopējo telpu, ko tas aizņem divdimensiju plaknē, nosaka ar īpašām formulām, pamatojoties uz malu skaitu un daudzstūra klasifikāciju. Laukuma formulas ir šādas:
| Daudzstūra apgabals | Formula |
|---|---|
| Trīsstūra laukums | 1/2 × Pamatne × augstums |
| Paralēlogrammas laukums | Pamatne × augstums |
| Taisnstūra laukums | Garums × platums |
| Laukuma laukums | (Sānos)2 |
| 1/2 × diagonāle1× diagonāle2 | |
| Trapeces apgabals | 1/2 × augstums × paralēlo malu summa |
| (5/2) × sānu garums × apotēms | |
| Sešstūra laukums | {(3√3)/2}puse2 |
| Septiņstūra apgabals | 3,643 × Sānu2 |
Daudzstūru perimetrs
Divdimensiju formas perimetrs attēlo tās ārējās robežas kopējo garumu. Daudzstūriem perimetru aprēķina šādi:
| Daudzstūra perimetrs | Formula |
|---|---|
| Trijstūra perimetrs | Trīs pušu summa |
| Paralēlogrammas perimetrs | 2 (blakus esošo malu summa) |
| Taisnstūra perimetrs | 2 (garums + platums) |
| Laukuma perimetrs | 4 × sāni |
| Romba perimetrs | 4 × sāni |
| Trapeces perimetrs | Paralēlo malu summa + neparalēlo malu summa |
| Pentagona perimetrs | 5 × sāni |
| Sešstūra perimetrs | 6 × sāni |
| Septiņstūra perimetrs | 7 × sāni |
Daudzstūra formulas diagonāle
Daudzstūra diagonāle ir līnijas segments, kas izveidots, savienojot divas virsotnes, kas nav blakus.
Diagonāļu skaits daudzstūrī = n(n-3)/2,
Kur “n” apzīmē daudzstūra malu skaitu.
Lasīt vairāk par Daudzstūra formulas diagonāle .
Leņķi daudzstūros
Ģeometrijā leņķi daudzstūros attiecas uz leņķiem, ko veido daudzstūra malas gan daudzstūra iekšpusē, gan ārpusē. Tādējādi daudzstūrī var būt abi leņķi, t.i.,
- Interjera leņķi
- Ārējie leņķi
Detalizēti apspriedīsim šo leņķu formulu šādi:
Daudzstūru iekšējā leņķa formula
Daudzstūra iekšējie leņķi ir tie, kas veidojas starp tā blakus esošajām malām un ir vienādi regulāra daudzstūra gadījumā. Iekšējo leņķu skaits atbilst daudzstūra malu skaitam.
Iekšējo leņķu “S” summu daudzstūrī ar “n” malām aprēķina kā
S = (n – 2) × 180°
Kur “n” apzīmē malu skaitu.
Daudzstūru ārējā leņķa formula
Katrs regulārā daudzstūra ārējais leņķis tiek veidots, pagarinot vienu no tā malām (pulksteņrādītāja virzienā vai pretēji pulksteņrādītāja virzienam) un izmērot leņķi starp šo paplašinājumu un blakus esošo malu. Regulārā daudzstūrī visi ārējie leņķi ir vienādi
Kopējā ārējo leņķu summa jebkurā daudzstūrī ir fiksēta 360°
Tāpēc
Katrs ārējais leņķis ir norādīts ar 360°/n
Kur “n” ir malu skaits.
Iekšējo un atbilstošo ārējo leņķu summa jebkurā daudzstūra virsotnē vienmēr ir 180 grādi, kas izsaka papildu attiecību:
Iekšējais leņķis + ārējais leņķis = 180°
Ārējais leņķis = 180° – iekšējais leņķis
Secinājums
- Daudzstūris ir slēgta figūra, ko ierobežo trīs vai vairāk līniju segmenti
- Iekšējo leņķu summa: Visu iekšējo leņķu summu n-šķautņu daudzstūrī nosaka pēc formulas (n–2) × 180°.
- Diagonāļu skaits: Daudzstūrim ar n malām diagonāļu skaitu aprēķina, izmantojot formulu n(n–3)/2.
- Trīsstūri, ko veido diagonāles: Trīsstūru skaits, kas veidojas, savienojot diagonāles no viena daudzstūra stūra, ir n–2.
- Regulāra daudzstūra iekšējais leņķis: Katra iekšējā leņķa mērs n-malu regulārā daudzstūrī ir {(n–2) × 180°}/n.
- Regulāra daudzstūra ārējais leņķis: Katra ārējā leņķa mērs n-šķautņu regulārā daudzstūrī ir 360°/n.
Arī Lasīt
- Kvadrāts
- Paralēlogramma
- Taisnstūris
Atrisināti piemēri par daudzstūri matemātikā
1. piemērs. Apsveriet četrstūri ar četrām malām. Atrodiet visu tā četrstūra iekšējo leņķu summu.
Risinājums:
Formula iekšējo leņķu summai n-malu regulārā daudzstūrī = (n − 2) × 180°
Četrstūra visu iekšējo leņķu summa = (4–2) × 180°
Četrstūra visu iekšējo leņķu summa = 2 × 180°
Četrstūra visu iekšējo leņķu summa = 360°
Tāpēc četrstūra visu iekšējo leņķu summa ir 360°.
2. piemērs. Apsveriet regulāru daudzstūri ar noteiktu ārējo un iekšējo leņķu attiecību 7:3. Nosakiet daudzstūra veidu.
Risinājums:
Ārējā un iekšējā leņķa attiecība ir 7:3.
Pieņemsim, ka daudzstūra ārējais un iekšējais leņķis ir 7x un 3x.
Jebkura daudzstūra ārējo un iekšējo leņķu summa ir 180°.
7x + 3x = 180°
10x = 180°
x = 18°
Ārējais leņķis = 18°
pārvērst in par virkni javaSānu skaits = 360°/ārējais leņķis
= 360°/18°
= 20
Tāpēc dotais daudzstūris ir ikosagons, jo tam ir 20 malas.
3. piemērs. Katrs daudzstūra ārējais leņķis mēra 90 grādus, nosakiet daudzstūra veidu?
Risinājums:
Saskaņā ar formulu katrs ārējais leņķis = 360°/n
Šeit n = malu skaits.
90°= 360°/n
n = 360°/90° = 4
Tādējādi attiecīgais daudzstūris ir četrstūris, jo tam ir četras malas.
4. piemērs: malas ir 10 m, 10 m, 8 m, 8 m, 5 m, 5 m, 9 m, 9 m. Cik metru virves būs nepieciešams Perimetram?
Risinājums:
Lai atrastu perimetram nepieciešamo virves garumu, mums jāsaskaita visu malu garumi:
Perimetrs = 10 m + 10 m + 8 m + 8 m + 5 m + 5 m + 9 m + 9 m
Perimetrs = 64 m.
Līdz ar to Perimetram kopumā būs nepieciešami 64 metri virves.
Praktizējiet jautājumus par daudzstūriem ģeometrijā
Tālāk ir sniegti daži prakses jautājumi, kuru pamatā ir daudzstūru formula:
Q1. Ja viens piecstūra leņķis ir 140°, nosakiet lielākā leņķa lielumu, ja pārējie leņķi ir attiecībā 1:2:3:4.
Q2. Ja daudzstūra iekšējo leņķu summa ir 160°, atrodiet daudzstūra malu skaitu.
Q3. Malu skaits divos regulāros daudzstūros ir proporcijā 2:3, un to iekšējo leņķu attiecība ir 4:5. Atrodiet šo daudzstūru attiecīgo malu skaitu.
Q4. Nosakiet septiņstūra leņķu kopējo summu.
Q5. Aprēķiniet piecstūra ārējo leņķu summu.
Q6. Cik malu ir sešstūrim?
- 4
- 6
- 8
- 10
Q7. Kurš no šiem nav regulārs daudzstūris?
- Trīsstūris
- Kvadrāts
- Pentagons
- Paralēlogramma
Bieži uzdotie jautājumi par daudzstūriem matemātikā
Kas ir daudzstūris matemātikā?
Matemātikā daudzstūris attiecas uz slēgtu divdimensiju figūru, ko veido trīs vai vairāku taisnu līniju savienojums. Termins daudzstūris ir atvasināts no grieķu valodas, un tas apzīmē daudzus un gon apzīmē leņķi.
Kurš ir mazākais daudzstūris?
Mazākais izveidots daudzstūris ir trīsstūris ar trim malām.
Kas ir 20-gon?
20 stūru ģeometrijā ir divdesmit malu daudzstūris.
Kāda ir daudzstūra ārējo leņķu kopējā summa?
Daudzstūra ārējo leņķu summa ir 360°.
Vai apli var klasificēt kā daudzstūri?
Daudzstūris ir slēgta forma, kas sastāv no taisnām līnijām. Aplis ir slēgta figūra, bet tā ir veidota no līknes. Tātad aplis nav daudzstūris.
Kāda ir daudzstūra iekšējā leņķa summa?
Daudzstūra iekšējā leņķa summa ir (n–2) × 180°, kur n ir daudzstūra malu skaits.
