logo

TechCodeview

Gausa procesa regresija (GPR)

Regresijas un varbūtības klasifikācijas problēmas var atrisināt, izmantojot Gausa procesu (GP), uzraudzītu mācību tehniku. Tā kā katru Gausa procesu var uzskatīt par daudzdimensiju bezgalīgu dimensiju vispārinājumu Gausa sadalījumi , nosaukumā parādās termins Gauss. Šajā amatā mēs apspriedīsim Gausa procesus regresijai, kas tiek saukta arī par Gausa procesa regresiju (GPR). Izmantojot GPR, ir atrisinātas daudzas reālās pasaules problēmas materiālzinātnes, ķīmijas, fizikas un bioloģijas jomās.

Satura rādītājs

Gausa procesa regresija (GPR)

Gausa procesa regresija (GPR) ir jaudīga un elastīga neparametriskas regresijas metode, ko izmanto mašīnmācība un statistika . Tas ir īpaši noderīgi, risinot problēmas, kas saistītas ar nepārtrauktiem datiem, kur attiecības starp ievades mainīgajiem un izvadi nav skaidri zināmas vai var būt sarežģītas. GPR ir Beijesa pieeja, kas var modelēt prognožu noteiktību, padarot to par vērtīgu rīku dažādām lietojumprogrammām, tostarp optimizācijai, laikrindu prognozēšanai un citiem. GPR pamatā ir Gausa procesa koncepcija, kas ir nejaušu mainīgo lielumu kopums, kuru jebkuram ierobežotam skaitam ir kopīgs Gausa sadalījums. Gausa procesu var uzskatīt par funkciju sadalījumu.



Gausa procesa regresijas (GPR) galvenie jēdzieni

Gaussain process

Neparametrisks, varbūtības modelis, ko sauc par a Gausa process (GP) tiek izmantots statistikā un mašīnmācībā regresijai, klasifikācijai un nenoteiktības kvantitatīvai noteikšanai. Tas attēlo nejaušu lielumu grupu, no kuriem katram ir kopīgs Gausa sadalījums un kuriem var būt ierobežots skaitlis. Ģimenes ārsti ir daudzpusīgs un efektīvs paņēmiens sarežģītu datu attiecību modelēšanai un prognožu sagatavošanai ar saistītu nenoteiktību.

Gausa procesu raksturojums :

  • Neparametrisks raksturs Ģimenes ārsti var pielāgoties datu sarežģītībai, jo viņi nepaļaujas uz noteiktu skaitu modeļa parametru
  • Varbūtības prognozes : ģimenes ārstu prognozes var noteikt kvantitatīvi, jo tās sniedz prognozes kā varbūtības sadalījumu.
  • Interpolācija un izlīdzināšana : ģimenes ārsti ir noderīgi trokšņainu vai neregulāri atlasītu datu gadījumā, jo tie labi spēj izlīdzināt trokšņainus datus un interpolēt starp datu punktiem.
  • Hiperparametru marginalizācija : likvidējot prasību par nepārprotamu hiperparametru pielāgošanu, tie tiek atstumti no hiperparametriem, padarot modeli vienkāršāku.

Vidējā funkcija

Katrā ievades punktā modelējamās funkcijas paredzamo vērtību attēlo ar vidējā funkcija Gausa procesos (GP). Tas darbojas kā pamata pieņēmums attiecībā uz pamatā esošo datu struktūru. Vidējā funkcija pēc noklusējuma bieži tiek iestatīta uz nulli, un to var mainīt, pamatojoties uz datu īpašībām vai domēna pieredzi. Ietekmējot prognožu centrālo tendenci, tas palīdz ģimenes ārstiem noteikt datu modeļus vai tendences. Ģimenes ārsti sniedz varbūtības prognozes, kas satur nenoteiktību, kā arī punktu aprēķinus, iekļaujot vidējo funkciju

Kovariācijas (kodola) funkcija

The kovariācijas funkcija , ko dēvē arī par kodola funkciju, mēra, cik līdzīgi ieejas datu punkti ir viens otram Gausa procesos (GP). Tas ir būtiski, lai raksturotu GP modeļa uzvedību, ietekmējot funkciju atlasi no iepriekšējā sadalījuma. Kovariācijas funkcija mēra pāru līdzības, lai noskaidrotu korelāciju starp funkciju vērtībām. Ģimenes ārsti var pielāgoties plašam datu modeļu klāstam, sākot no vienmērīgām tendencēm līdz sarežģītām struktūrām, jo ​​dažādas kodola funkcijas uztver dažāda veida korelācijas. Modeļa veiktspēju var ievērojami ietekmēt kodola izvēle.

Iepriekšējie izplatījumi

The iepriekšēja izplatīšana , Gausa procesos (GP) ir mūsu izpratne par funkcijām pirms jebkādu datu novērošanas. Parasti to apraksta ar kovariācijas (kodola) funkciju un vidējo funkciju. Kamēr kovariācijas funkcija apraksta funkciju vērtību līdzību vai korelāciju dažādos ievades punktos, vidējā funkcija kodē mūsu iepriekšējās cerības. To iepriekš izmanto ģimenes ārsti, lai izveidotu sadalījumu pa funkcijām. Ģimenes ārstiem priorus var atlasīt, lai attēlotu datu nenoteiktību, integrētu domēna zināšanas vai norādītu gludumu.

Aizmugurējie sadalījumi

Gausa procesi' vēlāka izplatīšana parāda mūsu pārskatītos pieņēmumus par funkcijām pēc datu novērošanas. Tas apkopo datu iespējamību, ņemot vērā funkciju un iepriekšējo sadalījumu. GP regresijas posteriors piedāvā sadalījumu pa funkcijām, kas visvairāk atbilst novērotajiem datiem. Pieļaujot varbūtības prognozes un nenoteiktības kvantitatīvo noteikšanu, aizmugurējais sadalījums atspoguļo kompromisu starp iepriekšējiem uzskatiem, kas saglabāti iepriekšējā sadalījumā, un informāciju, ko sniedz dati.

Gausa procesa regresijas (GPR) matemātiskā koncepcija

Regresijas uzdevumiem tiek izmantots neparametrisks, varbūtības mašīnmācīšanās modelis, ko sauc par Gausa procesa (GP) regresiju. Modelējot sarežģītas un neskaidras mijiedarbības starp ievades un izvades mainīgajiem, tas ir spēcīgs rīks. Tiek pieņemts, ka daudzfaktoru Gausa sadalījums rada datu punktus GP regresijā, un mērķis ir izsecināt šo sadalījumu.

kā izdzēst kolonnu postgresql

GP regresijas modelim ir šāda matemātiskā izteiksme. Pieņemsim, ka x1, x2,…..,xnir ievades datu punkti , kur x pieder reāliem skaitļiem (-2,-1,0,1…), (xiepsilon R)

Pieņemsim, ka y1, un2 ,……., unnir izejas vērtības, kur yipieder reālajam skaitlim (yiepsilon R)

GP regresijas modelis pieņem, ka Gausa process ar vidējo funkciju (mu ) un kovariācijas funkcija (k) nodrošina funkciju f, kas savieno ieejas ar izejām.

Pēc tam testa vietu komplektā x* f sadalījumu nosaka:

f(x^*) ∼ N(mu(x^*), k(x^*, x^*))

Parasti kodola funkcijas tiek izmantotas, lai definētu vidējo funkciju un kovariācijas funkciju. Piemēram, eksponenciālais kodols kvadrātā, ko bieži izmanto, ir aprakstīts šādi:

k(x_{i},x_{j}) = sigma^2 exp(-frac{||x_{i} – x_{j}||^2}{2l^2})

kur,

  • k(x_{i}, x_{j}) = Kodola funkcija tiek attēlota ar šo, un tā aprēķina korelāciju vai līdzību starp diviem ievades datu punktiem, xiun xj.
  • sigma^2 = Kodola dispersijas parametrs ir šāds. Tas nosaka kodola funkcijas mērogu vai vertikālo izplatību. Tas regulē, cik cieši datu punkti ir korelēti. A augstākssigma^2 nodrošina kodola funkciju ar lielāku dispersiju.
  • exp: eksponenciālā funkcija ir atbildīga par e paaugstināšanu līdz argumenta jaudai.
  • ||x_{i} – x_{j}||^2 : starpība starp ievades datu punktiem, xiun xj, ir Eiklīda attālums kvadrātā. Tiek mērīta ģeometriskā atdalīšana starp punktiem pazīmju telpā.
  • l2: Šis ir kodola garuma skalas vai raksturīgā garuma attēlojums. Tas regulē kodola funkcijas pasliktināšanās ātrumu, kad datu punkti atrodas tālāk viens no otra. Zemāks l izraisa kodola ātrāku degradāciju.

GP regresijas modelis izmanto Bajesa secinājumus, lai noteiktu f sadalījumu, kas, visticamāk, ir radījis datus, ņemot vērā apmācības datu kopu (x, y). Lai to izdarītu, ir jāaprēķina f posterior sadalījums, kas tiek definēts šādi:

p(f|x,y) =frac x,f)p(f) x)

powershell daudzrindu komentārs

kur datu marginālā varbūtība ir p(y|x), f iepriekšējais sadalījums ir p(f), un datu iespējamība, ja funkcija f ir (y|x,f).

Pēc f aizmugurējā sadalījuma apguves modelis aprēķina aizmugurējo paredzamo sadalījumu, lai veiktu prognozes papildu testa punktos x*. To var definēt šādi:

p(f^*|x^*, y,x) = int p(f^*|x^*, f), p(f|y,x)df

kur,

  • p(f^*|x*, y, x) = Tas parāda, ņemot vērā apmācības datus y un x, prognozēto funkciju vērtību f nosacīto varbūtību*svaigā ievades punktā x*Citiem vārdiem sakot, tas ir varbūtības sadalījums pa visām potenciālajām funkciju vērtībām jaunajā ievades vietā x*, ko nosaka novērotie dati y un to atbilstošās ievades vietas x.
  • int p(f^*|x^*, f)p(f|y,x)df = Šajā vienādojuma sadaļā tiek izmantots integrālis, lai noteiktu nosacīto varbūtību. Integrālis ietver visas funkcijas f potenciālās vērtības.
  • p(f^*|x^*, f) = Šis ir sagaidāmo funkciju vērtību f nosacītais varbūtības sadalījums*pie x*, ņemot vērā funkciju vērtības f dažās starpvietās.
  • p(f|y,x) = Ņemot vērā novērotos datus (y) un to ievades vietas (x), tas ir funkcijas vērtību (f) nosacītais varbūtības sadalījums.

Tādiem uzdevumiem kā lēmumu pieņemšana, apzinoties nenoteiktību un aktīva mācīšanās, šis sadalījums piedāvā prognozes nenoteiktības mērauklu, kas var būt noderīgs.

jvm java

Gausa procesa regresijas soļi

  • Datu vākšana : apkopojiet ievades-izejas datu pārus savai regresijas problēmai.
  • Izvēlieties kodola funkciju : atlasiet savai problēmai atbilstošu kovariācijas funkciju (kodolu). Kodola izvēle ietekmē to funkciju formu, kuras var modelēt GPR.
  • Parametru optimizācija : Novērtējiet kodola funkcijas hiperparametrus, maksimāli palielinot datu iespējamību. To var izdarīt, izmantojot optimizācijas metodes, piemēram, gradienta nolaišanos.
  • Prognoze: Ņemot vērā jaunu ievadi, izmantojiet apmācīto GPR modeli, lai veiktu prognozes. GPR nodrošina gan prognozēto vidējo, gan saistīto nenoteiktību (dispersiju).

Gausa procesa regresijas (GPR) ieviešana

Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()>

Izvade:

gpr-Geeksforgeeks

Šajā kodā vispirms ģenerējiet dažus datu paraugu punktus ar pievienotu troksni, pēc tam definējiet RBF kodolu un izveidojiet a Gausa procesa regresors ar to. Modelis tiek apmācīts, pamatojoties uz apmācības datiem, un tiek izmantots, lai prognozētu testa datus. Visbeidzot, rezultāti tiek vizualizēti ar diagrammu, kurā parādīti apmācības dati, prognozētais vidējais un 95% ticamības intervāls.

Gausa procesa ieviešana Python

Scikit Learn

Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)>

Ar šo kodu tiek importētas vajadzīgās bibliotēkas Gausa procesa regresijai (GPR) Python; šie ir SciPy lineārām algebras funkcijām, NumPy skaitliskām operācijām un Matplotlib datu vizualizācijai. Lai pārliecinātos, ka tas ir saderīgs ar nepieciešamajām pakotnēm, tas papildus pārbauda Python versiju un izdrukā to kopā ar NumPy un scikit-learn (sklearn) versijām.

Kodola atlase

Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, ' ')>

Izvade:

[RBF(garuma_mērogs=1),
RationalQuadratic (alfa=1, garuma_mērogs=1),
ExpSineSquared(garuma_mērogs=1, periodiskums=10),
DotProduct(sigma_0=1)** 2,
Mātes(garuma_mērogs=1, nu=1,5)]

Kods norāda pārbaudes vietu skaitu (n) un inicializē a nejauša sēkla . Lai parādītu izvēlētos kodolus, tas ģenerē vairāku kodola funkciju sarakstu un izdrukā sarakstu.

virkne masīvā c

Kodola salīdzināšana un vizualizācija

Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, ' ')>

Izvade:

RBF

graph-1-Geeksforgeeks

gp.kernel_ RBF(garuma_mērogs=1,93)
gp.log_marginal_likelihood: -3,444937833462133
-------------------------------------------------- -

Racionāls kvadrāts

graph-2-Geeksforgeeks

gp.kernel_ RationalQuadratic(alfa=1e+05, garuma_mērogs=1,93)
gp.log_marginal_likelihood: -3,4449718909150966
--------------------------------------------------

ExpSineSquared

graph-3-Geeksforgeeks

gp.kernel_ ExpSineSquared(garuma_mērogs=0,000524, periodiskums=2,31e+04)
gp.log_marginal_likelihood: -3,4449381454930217
--------------------------------------------------

Punktu produkts

graph-4-Geeksforgeeks

gp.kernel_ DotProduct(sigma_0=0,998)** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------

Mātes

graph-5-Geeksforgeeks

gp.kernel_ Matern(garuma_mērogs=1,99, nu=1,5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------

Kods sākas ar cilpu pāri dažādām kodola funkcijām, kas norādītas sarakstā kernel_. Gausa procesa regresors (gp) tiek izveidots, izmantojot konkrēto kodolu katram kodolam. Gausa procesam tas nosaka kovariācijas struktūru. Lai novērtētu iepriekšējo sadalījumu, tiek izveidota testa ievades punktu kopa ar nosaukumu x_test ar vērtībām no -5 līdz 5. Šī punktu kopa tiek pārveidota par kolonnas vektoru.

k tuvākais kaimiņš

Izmantojot gp.predict metodi, katrā testa punktā nosaka iepriekšējā sadalījuma vidējo (mu_prior) un standarta novirzi (sd_prior). Standarta novirzes vērtības tiek pieprasītas, izmantojot opciju return_std=True. gp.sample_y (x_test, 3) tiek izmantots, lai iegūtu trīs funkciju paraugus no iepriekšējā sadalījuma.

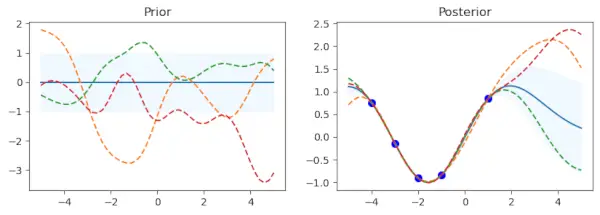
Pirmajā apakšgrafikā ir parādīts iepriekšējā sadalījuma vidējais lielums ar standarta novirzi, ko attēlo iekrāsots laukums. Paraugi ir uzlikti kā pārtrauktas līnijas, bet vidējais rādītājs tiek parādīts kā nepārtraukta līnija. Ir apakšgabals ar nosaukumu Prior. Ir definēts treniņu datu punktu kopums (x_train) un mērķa vērtības (y_train), kas tiem ir pievienots. Gausa procesa modelis ir aprīkots, izmantojot šos punktus (gp.fit(x_train, y_train)). Pieci datu punkti ar atbilstošām sinusa vērtībām veido apmācības datus šajā kodā.

Pēc apmācības datu pielāgošanas fāzes procedūra aprēķina aizmugurējā sadalījuma vidējo (mu_post) un standarta novirzi (sd_post) tiem pašiem testa punktiem (x_test). gp.sample_y(x_test, 3) tiek izmantots arī, lai izveidotu funkciju paraugus no aizmugurējā sadalījuma. Otrais apakšgrafiks pārklāj atlasītās funkcijas kā punktētas līnijas un parāda aizmugurējā sadalījuma vidējo vērtību, kas iekrāsota ar standarta novirzi. Apmācības datu punkti ir attēloti zilā krāsā. Apakšsižetam ir nosaukums Posterior.

Lai skatītu pašreizējā kodola iepriekšējo un aizmugurējo grafiku un iegūtu vizuālu izpratni par modeļa uzvedību, izsauciet Matplotlib funkciju plt.show().

Kods parāda informāciju par pašreizējo kodolu, piemēram, gp.kernel_, kas norāda pašreizējo izmantoto kodolu, un gp.log_marginal_likelihood (gp.kernel_.theta), kas nodrošina modeļa logaļējo varbūtību, izmantojot pašreizējo kodolu, pēc katras iepriekšējo un aizmugurējo diagrammu kopas.

Gausa procesa regresijas (GPR) priekšrocības

Gausa procesa regresijai (GPR) ir vairākas priekšrocības dažādos lietojumos:

  • GPR nodrošina regresijas varbūtības ietvaru, kas nozīmē, ka tas ne tikai sniedz punktu aplēses, bet arī nodrošina prognožu nenoteiktības aprēķinus.
  • Tas ir ļoti elastīgs un var ietvert sarežģītas attiecības datos.
  • GPR var pielāgot dažādām lietojumprogrammām, tostarp laika rindu prognozēšanai, optimizācijai un Bajesa optimizācijai.

Gausa procesa regresijas (GPR) izaicinājumi

  • GPR var būt skaitļošanas ziņā dārgs, strādājot ar lielām datu kopām, jo ​​ir nepieciešama kovariācijas matricas inversija.
  • Kodola funkcijas un tās hiperparametru izvēle var būtiski ietekmēt modeļa veiktspēju.

Labi GPR lietojumprogrammu piemēri

  • Akciju cenas prognoze: GPR var izmantot, lai modelētu un prognozētu akciju cenas, ņemot vērā nepastāvību un nenoteiktību finanšu tirgos.
  • Datoru eksperimenti: GPR ir noderīga, lai optimizētu sarežģītas simulācijas, modelējot ievades-izejas attiecības un identificējot visietekmīgākos parametrus.
  • Anomāliju noteikšana: GPR var izmantot anomāliju noteikšanai, kur tā identificē neparastus modeļus laikrindu datos, tverot normālu datu sadalījumu.

Secinājums

Noslēgumā jāsaka, ka Gausa procesa regresija ir vērtīgs rīks datu analīzei un prognozēšanai situācijās, kad ir svarīgi saprast prognožu nenoteiktību. Izmantojot varbūtības modelēšanu un kodola funkcijas, GPR var nodrošināt precīzus un interpretējamus rezultātus. Tomēr, ieviešot GPR praksē, ir ļoti svarīgi ņemt vērā skaitļošanas izmaksas un vajadzību pēc ekspertu ieguldījuma.