BINĀRĀ KAUDZE — TECHCODEVIEW.COM - IT PROBLĒMAS UN RISINĀJUMI

A Binārā kaudze ir pilnīgs binārais koks ko izmanto datu efektīvai glabāšanai, lai iegūtu maksimālo vai minimālo elementu, pamatojoties uz tā struktūru.

Binārā kaudze ir vai nu minimālā kaudze, vai maksimālā kaudze. Minimālajā binārajā kaudzē atslēgai saknē ir jābūt minimālai starp visām binārajā kaudzē esošajām atslēgām. Tam pašam rekvizītam ir jābūt rekursīvi patiesam visiem binārā koka mezgliem. Max Binary Heap ir līdzīgs MinHeap.

Min Heap piemēri:

10 10
/ /
20 100 15 30
// /
30 40 50 100 40

Kā tiek attēlota binārā kaudze?

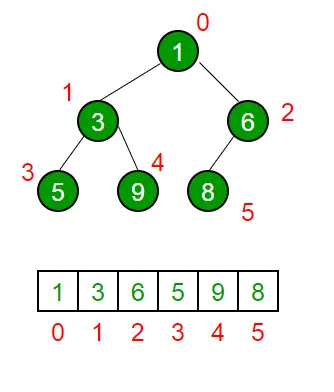
Binārā kaudze ir a Pilnīgs binārais koks . Binārā kaudze parasti tiek attēlota kā masīvs.

Saknes elements atradīsies Arr[0].
Zemāk esošajā tabulā ir parādīti citu i mezglu indeksi^thmezgls, t.i., Arr[i]:

Arr[(i-1)/2]	Atgriež vecākmezglu
Arr[(2*i)+1]	Atgriež kreiso bērnmezglu
Arr[(2*i)+2]	Atgriež pareizo pakārtoto mezglu

Šķērsošanas metode, ko izmanto, lai panāktu masīva attēlojumu, ir Līmeņa pasūtījumu izbraukšana . Lūdzu atsaucies uz Binārās kaudzes masīva attēlojums sīkākai informācijai.

Binārais kaudzes koks

Darbības ar Heap:

Tālāk ir norādītas dažas standarta darbības ar minimālo kaudzi:

getMin(): Tas atgriež Min Heap saknes elementu. Laiks Šīs operācijas sarežģītība ir O(1) . Maxheap gadījumā tā būtu getMax() .
ekstraktsMin() : No MinHeap noņem minimālo elementu. Šīs operācijas sarežģītības laiks ir O(log N) jo šai darbībai ir jāsaglabā kaudzes īpašums (zvanot kaudze () ) pēc saknes noņemšanas.
samazinātKey() : Samazina atslēgas vērtību. Šīs operācijas laika sarežģītība ir O(log N) . Ja mezgla samazinātā atslēgas vērtība ir lielāka par mezgla vecāku, mums nekas nav jādara. Pretējā gadījumā mums ir jāpārvietojas augšup, lai labotu bojāto kaudzes īpašumu.
ievietot () : Jaunas atslēgas ievietošana prasa O(log N) laiks. Mēs pievienojam jaunu atslēgu koka galā. Ja jaunā atslēga ir lielāka par tās vecāku, mums nekas nav jādara. Pretējā gadījumā mums ir jāpārvietojas augšup, lai labotu bojāto kaudzes īpašumu.
dzēst() : Nepieciešama arī atslēgas dzēšana O(log N) laiks. Dzēšamo atslēgu nomainām ar minimālo bezgalīgo zvanot samazinātKey() . Pēc downKey() mīnus bezgalīgajai vērtībai ir jāsasniedz sakne, tāpēc mēs izsaucam ekstraktsMin() lai izņemtu atslēgu.

Zemāk ir sniegta pamata kaudzes operāciju īstenošana.

C++

// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>

'
Overflow: Could not insertKey
'>

;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>harr[i])>> {> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>harr[i])>> {> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest != i)   {   swap(&harr[i], &harr[smallest]);   MinHeapify(smallest);   }  }    // A utility function to swap two elements  void swap(int *x, int *y)  {   int temp = *x;   *x = *y;   *y = temp;  }    // Driver program to test above functions  int main()  {   MinHeap h(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   cout << h.extractMin() << ' ';   cout << h.getMin() << ' ';   h.decreaseKey(2, 1);   cout << h.getMin();   return 0;  }>

int uz virkni c++

Java

// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0>

&& heapArray[i]   swap(heapArray, i, parent(i));   i = parent(i);   }   return true;   }     // Decreases value of given key to new_val.   // It is assumed that new_val is smaller   // than heapArray[key].   public void decreaseKey(int key, int new_val) {   heapArray[key] = new_val;     while (key != 0 && heapArray[key]   swap(heapArray, key, parent(key));   key = parent(key);   }   }     // Returns the minimum key (key at   // root) from min heap   public int getMin() {   return heapArray[0];   }       // Method to remove minimum element   // (or root) from min heap   public int extractMin() {   if (current_heap_size <= 0) {   return Integer.MAX_VALUE;   }     if (current_heap_size == 1) {   current_heap_size--;   return heapArray[0];   }     // Store the minimum value,   // and remove it from heap   int root = heapArray[0];     heapArray[0] = heapArray[current_heap_size - 1];   current_heap_size--;   MinHeapify(0);     return root;   }     // This function deletes key at the   // given index. It first reduced value   // to minus infinite, then calls extractMin()   public void deleteKey(int key) {   decreaseKey(key, Integer.MIN_VALUE);   extractMin();   }     // A recursive method to heapify a subtree   // with the root at given index   // This method assumes that the subtrees   // are already heapified   private void MinHeapify(int key) {   int l = left(key);   int r = right(key);     int smallest = key;   if (l   smallest = l;   }   if (r   smallest = r;   }     if (smallest != key) {   swap(heapArray, key, smallest);   MinHeapify(smallest);   }   }     // Increases value of given key to new_val.   // It is assumed that new_val is greater   // than heapArray[key].   // Heapify from the given key   public void increaseKey(int key, int new_val) {   heapArray[key] = new_val;   MinHeapify(key);   }     // Changes value on a key   public void changeValueOnAKey(int key, int new_val) {   if (heapArray[key] == new_val) {   return;   }   if (heapArray[key]   increaseKey(key, new_val);   } else {   decreaseKey(key, new_val);   }   }  }    // Driver Code  class MinHeapTest {   public static void main(String[] args) {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);   System.out.print(h.extractMin() + ' ');   System.out.print(h.getMin() + ' ');     h.decreaseKey(2, 1);   System.out.print(h.getMin());   }  }    // This code is contributed by rishabmalhdijo>

Python

# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)>

python kortežs sakārtots

C#

// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if>

(l   heapArray[l]   {   smallest = l;   }   if (r   heapArray[r]   {   smallest = r;   }     if (smallest != key)   {   Swap(ref heapArray[key],   ref heapArray[smallest]);   MinHeapify(smallest);   }  }    // Increases value of given key to new_val.  // It is assumed that new_val is greater  // than heapArray[key].  // Heapify from the given key  public void increaseKey(int key, int new_val)  {   heapArray[key] = new_val;   MinHeapify(key);  }    // Changes value on a key  public void changeValueOnAKey(int key, int new_val)  {   if (heapArray[key] == new_val)   {   return;   }   if (heapArray[key]   {   increaseKey(key, new_val);   } else  {   decreaseKey(key, new_val);   }  }  }    static class MinHeapTest{    // Driver code  public static void Main(string[] args)  {   MinHeap h = new MinHeap(11);   h.insertKey(3);   h.insertKey(2);   h.deleteKey(1);   h.insertKey(15);   h.insertKey(5);   h.insertKey(4);   h.insertKey(45);     Console.Write(h.extractMin() + ' ');   Console.Write(h.getMin() + ' ');     h.decreaseKey(2, 1);   Console.Write(h.getMin());  }  }    // This code is contributed by  // Dinesh Clinton Albert(dineshclinton)>

Javascript

git statuss -s

// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && arr[>this>.parent(i)]>arr[i])>> {> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>arr[i])>> {> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if>

(l   smallest = l;   if (r   smallest = r;   if (smallest !== i)   {   [arr[i], arr[smallest]] = [arr[smallest], arr[i]]   this.MinHeapify(smallest);   }   }  }    let h = new MinHeap();   h.insert(3);   h.insert(2);   h.deleteKey(1);   h.insert(15);   h.insert(5);   h.insert(4);   h.insert(45);     console.log(h.extractMin() + ' ');   console.log(h.getMin() + ' ');     h.decreaseKey(2, 1);   console.log(h.extractMin());>

Izvade

2 4 1>

Kaudzīšu pielietojumi:

Kaudzes kārtošana : Heap Sort izmanto Binary Heap, lai kārtotu masīvu pēc O(nLogn) laika.
Prioritātes rinda: Prioritārās rindas var efektīvi ieviest, izmantojot Binary Heap, jo tā atbalsta insert(), delete() un extractmax(), deseKey() operācijas O(log N) laikā. Binomiālā kaudze un Fibonači kaudze ir binārā kaudzes varianti. Šīs variācijas arī efektīvi apvieno.
Grafu algoritmi: prioritārās rindas tiek īpaši izmantotas, piemēram, diagrammu algoritmos Dijkstras īsākais ceļš un Prim minimālais aptverošais koks .
Daudzas problēmas var efektīvi atrisināt, izmantojot Heaps. Piemēram, skatiet tālāk norādīto. a) K’th lielākais elements masīvā . b) Kārtot gandrīz sakārtotu masīvu/ c) Apvienot K sakārtotos masīvus .

Saistītās saites:

Kodēšanas prakse uz Heap
Visi raksti par kaudzi
PriorityQueue: binārā kaudzes ieviešana Java bibliotēkā