Mēs zinām a koks ir nelineāra datu struktūra. Tajā nav bērnu skaita ierobežojumu. AKas ir pilnīgs binārais koks?

Pilnīgs binārais koks ir īpašs binārā koka veids, kurā visi koka līmeņi ir pilnībā aizpildīti, izņemot zemākā līmeņa mezglus, kas tiek aizpildīti no pēc iespējas kreisās puses.

Pilnīgs binārais koks

Daža pilnīga binārā koka terminoloģija:

• Sakne – Mezgls, kurā neviena mala nenāk no vecāka. Piemērs mezgls A
• Bērns – Mezglu, kuram ir kāda ienākošā mala, sauc par bērnu. Piemērs – mezgli B, F ir attiecīgi A un C atvases.
• Brālis un māsa – Mezgli, kuriem ir viens un tas pats vecāks, ir brāļi un māsas. Piemērs - D, E ir brāļi un māsas, jo viņiem ir viens un tas pats vecāks B.
• Mezgla pakāpe – Konkrēta vecāka bērnu skaits. Piemērs - A pakāpe ir 2 un C pakāpe ir 1. D pakāpe ir 0.
• Iekšējie/ārējie mezgli – Lapu mezgli ir ārējie mezgli, un mezgli, kas nav lapu mezgli, ir iekšējie mezgli.
• Līmenis - Saskaitiet mezglus ceļā, lai sasniegtu galamērķa mezglu. Piemērs - mezgla D līmenis ir 2, jo mezgli A un B veido ceļu.
• Augstums – Malu skaits, lai sasniegtu galamērķa mezglu, saknes augstums ir 0. Piemērs – Mezgla E augstums ir 2, jo tam ir divas malas no saknes.

Pilnīga binārā koka īpašības:

• Tiek uzskatīts, ka pilnīgs binārais koks ir īsts binārs koks, kurā visām lapām ir vienāds dziļums.
• Pilnā binārā kokā mezglu skaits dziļumā d ir 2 ^d .
• Pilnīgā binārā kokā ar n mezglu augstums koka ir žurnāls(n+1) .
• Visi līmeņi izņemot pēdējo līmeni ir pilnībā pilnas.

Ideāls binārais koks pret pilnu bināro koku:

Binārs koks ar augstumu “h” ar maksimālo mezglu skaitu ir a ideāls binārais koks.
Noteiktam augumam h , maksimālais mezglu skaits ir 2 ^h+1 -1 .

A pabeigt binārais koks ar augstumu h ir ideāls binārais koks līdz augstumam h-1 , un pēdējā līmeņa elementi tiek saglabāti secībā no kreisās puses uz labo.

1. piemērs:

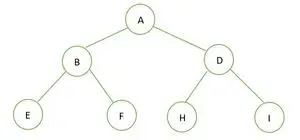
Binārs koks

Dotā binārā koka augstums ir 2 un maksimālais mezglu skaits šajā kokā ir n= 2^h+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Līdz ar to mēs varam secināt, ka tā ir ideāls binārais koks .
Tagad pilnīgam bināram kokam tas ir pilns līdz augstumam h-1 t.i.; 1, un pēdējā līmeņa elementi tiek saglabāti secībā no kreisās uz labo pusi. Tādējādi tas ir arī pilnīgs binārais koks. Šeit ir elementu attēlojums, kad tie tiek glabāti masīvā

Elements tiek saglabāts masīvā līmenī pēc līmeņa

Masīvā visi elementi tiek glabāti nepārtraukti.

2. piemērs:

nullpointerizņēmums

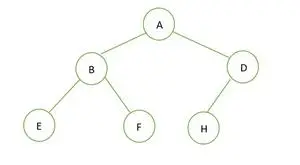
Binārs koks

Dotā binārā koka augstums ir 2, un maksimālais mezglu skaits, kam tajā vajadzētu būt, ir 2^h+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Bet mezglu skaits kokā ir 6 . Tāpēc tā ir nav ideāls binārais koks .
Tagad pilnīgam bināram kokam tas ir pilns līdz augstumam h-1 t.i.; 1 , un pēdējais līmeņa elements tiek saglabāti secībā no kreisās puses uz labo. Tāpēc šis ir a pilnīgs binārais koks . Saglabājiet elementu masīvā, un tas būs līdzīgs;

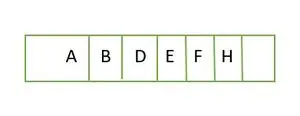
Elements tiek saglabāts masīvā līmenī pēc līmeņa

3. piemērs:

Aktieris Reha

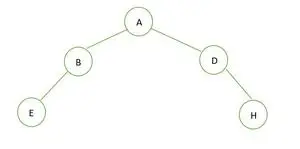
Binārs koks

Binārā koka augstums ir 2, un maksimālais mezglu skaits, kas tajā var būt, ir 7, taču ir tikai 5 mezgli, tāpēc tas ir nav ideāls binārais koks .
Pilna binārā koka gadījumā mēs redzam, ka pēdējā līmenī elementi netiek aizpildīti secībā no kreisās uz labo. Tā tas ir nav pilnīgs binārs koks .

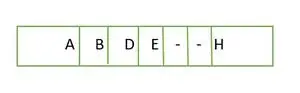
Elements tiek saglabāts masīvā līmenī pēc līmeņa

Elementi masīvā nav nepārtraukti.

Pilns binārais koks pret pilnu bināro koku:

Pilnam binārajam kokam katram mezglam ir vai nu 2 bērni, vai 0 bērnu.

1. piemērs:

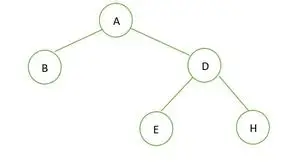
Binārs koks

Dotajā binārajā kokā nav neviena mezgla ar 1 pakāpi, vai nu 2 vai 0 bērnu katram mezglam, tāpēc tas ir pilns binārs koks .

Pilnam binārajam kokam elementi tiek glabāti pa līmeņiem, nevis no pēdējā līmeņa kreisās puses. Tāpēc tas ir nav pilnīgs binārs koks . Masīva attēlojums ir:

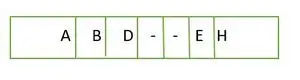
Elements tiek saglabāts masīvā līmenī pēc līmeņa

2. piemērs:

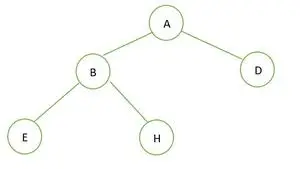
Binārs koks

Dotajā binārajā kokā nav neviena mezgla ar 1. pakāpi. Katram mezglam ir 2 vai 0 pakāpe. Tādējādi tas ir pilns binārais koks .

Pilnam binārajam kokam elementi tiek saglabāti pa līmeņiem un aizpildīti no pēdējā līmeņa kreisās puses. Līdz ar to šis a pilnīgs binārais koks . Zemāk ir koka masīva attēlojums:

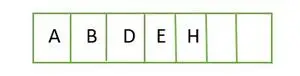
Elements tiek saglabāts masīvā līmenī pēc līmeņa

3. piemērs:

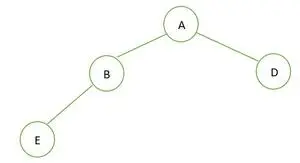
Binārs koks

Dotajā binārā koka mezglā B ir 1. pakāpe, kas pārkāpj pilna binārā koka īpašību, tāpēc tas ir nav pilnīgs Binārais koks

jsp

Pilnam binārajam kokam elementi tiek saglabāti pa līmeņiem un aizpildīti no pēdējā līmeņa kreisās puses. Tāpēc šis ir a pilnīgs binārais koks . Binārā koka masīva attēlojums ir:

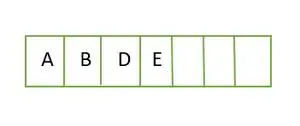
Elements tiek saglabāts masīvā līmenī pēc līmeņa

4. piemērs:

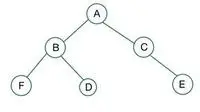
binārs koks

Dotajā binārā koka mezglā C ir 1. pakāpe, kas pārkāpj pilna binārā koka īpašību, tāpēc tas ir nav pilnīgs Binārais koks

Pilnam binārajam kokam elementi tiek saglabāti pa līmeņiem un aizpildīti no pēdējā līmeņa kreisās puses. Šeit mezgls E pārkāpj nosacījumu. Tāpēc tas ir nav pilnīgs binārs koks .

Pilnīga binārā koka izveide:

Mēs zinām a pilnīgs binārais koks ir koks, kurā, izņemot pēdējo līmeni (teiksim l )visam citam līmenim ir ( 2l ) mezgli un mezgli ir sakārtoti no kreisās puses uz labo pusi.
To var attēlot, izmantojot masīvu. Ja vecāks ir tas indekss i tātad kreisais bērns ir plkst 2i+1 un īstais bērns ir plkst 2i+2 .

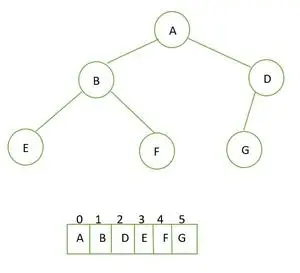
Pilnīgs binārais koks un tā masīva attēlojums

xdxd nozīme

Algoritms:

Lai izveidotu a Pilnīgs binārais koks , mums ir nepieciešams a 1. darbība: Inicializējiet sakni ar jaunu mezglu, kad koks ir tukšs.

2. darbība: Ja koks nav tukšs, iegūstiet priekšējo elementu

• Ja priekšējam elementam nav kreisā bērna, iestatiet kreiso bērnu uz jaunu mezglu
• Ja pareizais bērns nav klāt, iestatiet pareizo bērnu kā jaunu mezglu

3. darbība: Ja mezglam ir abi bērni, tad pop to no rindas.

4. darbība: Ievietojiet jaunos datus rindā.

Ilustrācija:

Apsveriet tālāk redzamo masīvu:

1. Pirmajam elementam būs sakne (vērtība indeksā = 0 )

A tiek pieņemts kā sakne

2. Nākamais elements (pie indeksa = 1 ) būs pa kreisi un trešais elements (indekss = 2 ) būs pareizais saknes bērns

B kā kreisais bērns un D kā labais bērns

java izņēmumi

3. ceturtais (indekss = 3 ) un piektais elements (indekss = 4 ) būs B mezgla kreisais un labais bērns

E un F ir B kreisās un labās puses bērni

4. Nākamais elements (indekss = 5 ) tiks atstāts mezgla D bērns

G ir izveidots D mezgla kreisais bērns

Šādi tiek izveidots pilnīgs binārais koks.

Īstenošana: Pilnīga binārā koka izveides īstenošanai no līmeņa secības šķērsošana ir dota šo ziņu .

Pilnīga binārā koka pielietojums:

• Kaudzes kārtošana
• Uz kaudzes kārtošanu balstīta datu struktūra

Pārbaudiet, vai dotais binārais koks ir pilnīgs vai nē: Sekojiet šo ziņu lai pārbaudītu, vai dotais binārais koks ir pilnīgs vai nē.