Trigonometrija ir svarīga matemātikas nozare, kas pēta attiecības starp taisnleņķa trijstūra leņķiem un malu garumiem. Sešas trigonometriskās attiecības vai funkcijas ir sinuss, kosinuss, tangenss, kosekants un sekants, un trigonometriskā attiecība ir attiecība starp taisnleņķa trijstūra malām. Sinusa, kosinusa un pieskares funkcijas ir trīs svarīgas trigonometriskās funkcijas, jo pārējās trīs, t.i., kosekantes, sekantes un kotangentes funkcijas, ir attiecīgi sinusa, kosinusa un pieskares funkciju abpusējas funkcijas.
- sin θ = pretējā puse/hipotenūza
- cos θ = Blakus puse/Hipotenūza
- iedegums θ = pretējā puse/blakuspuse
- cosec θ = hipotenūza/pretēja puse
- sec θ = hipotenūza/blakus puse
- gultiņa θ = blakus puse/pretējā puse
Pieskares funkcija ir viena no 6 izmantotajām trigonometriskajām funkcijām trigonometrijas formulas .
Satura rādītājs
Pieskares formula
Leņķa pieskares taisnleņķa trijstūrī ir pretējās malas garuma attiecība pret blakus esošās malas garumu pret doto leņķi. Pieskares funkciju rakstām kā iedegumu. Apskatīsim taisnleņķa trīsstūri XYZ, un viens no tā asajiem leņķiem ir θ. Pretēja puse ir mala, kas ir pretēja leņķim θ, un blakus esošā puse ir mala, kas atrodas blakus leņķim θ.
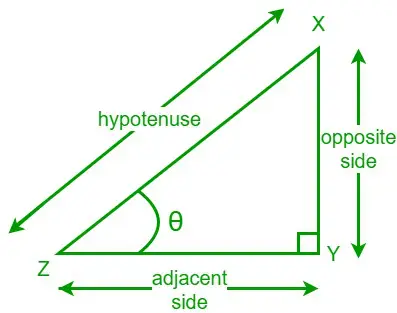
Tagad dotā leņķa θ pieskares formula ir,
iedegums θ = pretējā puse/blakuspuse
Dažas pamata pieskares formulas
Pieskares funkcija kvadrantos
Pieskares funkcija ir pozitīva pirmajā un trešajā kvadrantā un negatīva otrajā un ceturtajā kvadrantā.
- iedegums (2π + θ) = iedegums θ (1stkvadrants)
- iedegums (π – θ) = – iedegums θ (2ndkvadrants)
- iedegums (π + θ) = iedegums θ (3rdkvadrants)
- iedegums (2π – θ) = – iedegums θ (4thkvadrants)
Pieskares funkcija kā negatīva funkcija
Pieskares funkcija ir negatīva funkcija, jo negatīvā leņķa tangensa ir pozitīvā pieskares leņķa negatīvā.
iedegums (-θ) = – iedegums θ
Pieskares funkcija sinusa un kosinusa funkcijas izteiksmē
Pieskares funkciju sinusa un kosinusa funkciju izteiksmē var uzrakstīt kā,
tan θ = sin θ/cos θ
Mēs zinām, ka iedegums θ = pretējā puse/blakuspuse
Tagad sadaliet gan skaitītāju, gan saucēju ar hipotenūzu
iedegums θ = (pretējā puse/hipotenūza)/(blakuspuse/hipotenūza)
Mēs zinām, ka grēks θ = pretējā puse/hipotenūza
cos θ = blakus esošā puse/hipotenūza
Tādējādi tan θ = sin θ/cos θ
Pieskares funkcija sinusa funkcijas izteiksmē
Pieskares funkciju sinusa funkcijas izteiksmē var uzrakstīt kā,
iedegums θ = sin θ/(√1 – grēks 2 i)
Mēs to zinām,
tan θ = sin θ/cos θ
kādi mēneši ir Q1
No Pitagora identitātēm mums ir,
bez2θ + cos2θ = 1
cos2θ = 1 – grēks2i
cos θ = √(1 – sin2i)
Tātad iedegums θ = grēks θ/(√1 – grēks2i)
Pieskares funkcija kosinusa funkcijas izteiksmē
Pieskares funkciju kosinusa funkcijas izteiksmē var uzrakstīt kā,
iedegums θ = (√1 -cos 2 i)/cos i
Mēs to zinām,
tan θ = sin θ/cos θ
No Pitagora identitātēm mums ir,
bez2θ + cos2θ = 1
bez2θ = 1 – cos2i
sin θ = √(1 – cos2i)
Tādējādi iedegums θ = (√1 – cos2i)/cos i
Pieskares funkcija kotangentes funkcijas izteiksmē
Pieskares funkciju kotangentes funkcijas izteiksmē var uzrakstīt kā,
iedegums θ = 1/gultiņa θ
vai
iedegums θ = bērnu gultiņa (90° – θ) (vai) gultiņa (π/2 – θ)
Pieskares funkcija kosekanta funkcijas izteiksmē
Pieskares funkciju kosekantu funkcijas izteiksmē var uzrakstīt kā,
iedeguma θ = 1/√ (kosek 2 es - 1)
No Pitagora identitātēm mums ir,
cosec2θ – bērnu gultiņa2θ = 1
bērnu gultiņa2θ = cosec2es - 1
bērnu gultiņa θ = √ (kosek2es - 1)
Mēs to zinām,
iedegums θ = 1/gultiņa θ
Tādējādi iedegums θ = 1/√ (kosek2es - 1)
Pieskares funkcija sekanta funkcijas izteiksmē
Pieskares funkciju sekanta funkcijas izteiksmē var uzrakstīt kā,
iedegums θ = √sek 2 es - 1
No Pitagora identitātēm mums ir,
sek2θ – tātad2θ = 1
iedegums θ = sek2es - 1
Tādējādi iedegums θ = √ (sek2es - 1)
Pieskares funkcija dubultā leņķa izteiksmē
Pieskares funkcija dubultam leņķim ir,
iedegums 2θ = (2 tan θ)/(1 – iedegums 2 i)
Pieskares funkcija trīskāršā leņķa izteiksmē
Trīskāršā leņķa pieskares funkcija ir,
iedegums 3θ = (3 tan θ – iedegums 3 θ) / (1–3 iedegums 2 i)
Pieskares funkcija pusleņķa izteiksmē
Pieskares funkcija pusleņķim ir,
iedegums (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
iedegums (θ/2) = (1 – cos θ) / ( sin θ)
Pieskares funkcija divu leņķu saskaitīšanas un atņemšanas izteiksmē
Pieskares funkcijas summas un starpības formulas ir,
iedegums (A + B) = (iedegums A + iedegums B)/(1 — iedegums A iedegums B)
iedegums (A–B) = (iedegums A — iedegums B)/(1 + iedegums A iedegums B)
Trigonometrisko attiecību tabula
| Leņķis (grādos) | Leņķis (radiānos) | grēks i | cos θ | tan θ = sin θ/cos θ | cosec θ | sek θ | gultiņa i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | nenoteikts | 1 | nenoteikts |
| 30° | p/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | p/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 q4 mēneši | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = nenoteikts | 1 | nenoteikts | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | nenoteikts | -1 | nenoteikts |
Atrisināts pieskares formulu piemērs
1. piemērs. Atrodiet tan θ vērtību, ja sin θ = 2/5 un θ ir pirmais kvadranta leņķis.
Risinājums:
Ņemot vērā,
- sin θ = 2/5
No Pitagora identitātēm, kas mums ir,
bez2θ + cos2θ = 1
cos2θ = 1 – grēks2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Tā kā θ ir pirmais kvadranta leņķis, cos θ ir pozitīvs.
cos θ = √21/5
Mēs to zinām,
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
iedeguma θ = 2√21/21
Tātad tan θ vērtība, kad sin θ = 2/5 un θ atrodas pirmajā kvadrantā, ir (2√21) /(21)
2. piemērs. Atrodiet tan x vērtību, ja sec x = 13/12 un x ir ceturtā kvadranta leņķis.
Risinājums:
Ņemot vērā, sek x = 13/12
No Pitagora identitātēm mums ir,
sek2x - tā2x = 1
tātad2x = sek2x – 1= (13/12)2- 1
tātad2x = (169/144) – 1 = 25/144
iedegums x = ± 5/12
Tā kā x ir ceturtā kvadranta leņķis, tan x ir negatīvs.
iedegums x = – 5/12
Tāpēc iedegums x = – 5/12
3. piemērs: ja iedegums X = 2/3 un iedegums Y = 1/2, tad kāda ir iedeguma (X + Y) vērtība?
ipconfig uz Ubuntu
Risinājums:
Ņemot vērā,
iedegums X = 2/3 un iedegums Y = 1/2
Mēs to zinām,
iedegums (X + Y) = (iedegums X + iedegums Y)/(1 — iedegums X iedegums Y)
iedegums (X + Y) = [(2/3) + (1/2)]/[1 – (2/3) × (1/2)]
= (7/6)/(2/3) = 7/4
Tāpēc iedegums(X + Y) = 7/4
4. piemērs: Aprēķiniet pieskares funkciju, ja taisnleņķa trijstūra blakus un pretējās malas ir attiecīgi 4 cm un 7 cm.
Risinājums:
Ņemot vērā,
Blakus esošā puse = 4 cm
Pretējā puse = 7 cm
Mēs to zinām,
iedegums θ = pretējā puse/blakuspuse
iedegums θ = 7/4 = 1,75
Tāpēc iedeguma θ = 1,75
5. piemērs: Vīrietis skatās uz pulksteņa torni 60° leņķī pret torņa virsotni, kura augstums ir 100 m. Kāds ir attālums starp cilvēku un torņa pamatni?
Risinājums:
Ņemot vērā,
Torņa augstums = 100 m un θ = 60°
Ļaujiet attālumam starp cilvēku un torņa pēdu = d
Mums ir,
iedegums θ = pretējā puse/blakuspuse
iedegums 60° = 100/d
√3 = 100/d [kopš, tātad 60° = √3]
d = 100/√3
Tāpēc attālums starp cilvēku un torņa pēdu ir 100/√3
6. piemērs: atrodiet tan θ vērtību, ja sin θ = 7/25 un sec θ = 25/24.
Risinājums:
Ņemot vērā,
sin θ = 7/25
sek θ = 25/24
Mēs to zinām,
sec θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Mums ir,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
Tāpēc iedeguma θ = 7/24
7. piemērs. Atrodiet tan θ vērtību, ja cosec θ = 5/3 un θ ir pirmais kvadranta leņķis.
Risinājums:
Dots, cosec θ = 5/3
No Pitagora identitātēm mums ir,
string.format javacosec2θ – bērnu gultiņa2θ = 1
bērnu gultiņa2θ = cosec2es - 1
bērnu gultiņa θ = (5/3)2– 1 = (25/9) – 1 = 16/9
bērnu gultiņa θ = ±√16/9 = ± 4/3
Tā kā θ ir pirmais kvadranta leņķis, gan kotangenses, gan tangenses funkcijas ir pozitīvas.
bērnu gultiņa θ = 4/3
Mēs to zinām,
bērnu gultiņa θ = 1/tan θ
4/3 = 1/tanθ
iedegums θ = 3/4
Tāpēc iedegums θ = 3/4
8. piemērs. Atrodiet tan 3θ, ja sin θ = 3/7 un θ ir pirmais kvadranta leņķis.
Risinājums:
Ņemot vērā, grēks θ = 12/13
No Pitagora identitātēm, kas mums ir,
bez2θ + cos2θ = 1
cos2θ = 1 – grēks2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Tā kā θ ir pirmais kvadranta leņķis, cos θ ir pozitīvs.
cos θ = 5/13
Mēs to zinām,
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Tādējādi iedegums θ = 12/5
Tagad mēs zinām, ka
iedegums 3θ = (3 tan θ – tan3θ) / (1–3 tan2θ)
iedegums 3θ = 3 × (12/5)

