Parabolas standarta forma ir y = ax²+ bx + c kur a, b un c ir reāli skaitļi un a nav vienāds ar nulli. Parabola ir definēta kā visu plaknes punktu kopa, kas atrodas vienādā attālumā no fiksētas līnijas un fiksēta punkta plaknē.

Šajā rakstā mēs detalizēti sapratīsim, kas ir parabola, parabolas standarta vienādojums, saistītie piemēri un citi.

Satura rādītājs

• Kas ir parabola?
• Parabolas vienādojums
• Parabolas vispārīgie vienādojumi
• Parabolas standarta vienādojumi
• Parabolas daļas
• Parabolas vienādojuma piemēri

Kas ir parabola?

Parabola ir konusa griezums, kas definēts kā visu punktu kopa, kas atrodas vienādā attālumā no punkta, ko sauc par fokusu, un līnijas, ko sauc par virzienu. Parabolas standarta vienādojumi ir atkarīgi no tās orientācijas (atvēršanas virziena) un stāvokļa.

Parabolas vienādojums

Parabolas vienādojumu var uzrakstīt standarta formā vai vispārīgā formā, un tie abi ir pievienoti zemāk:

Parabolas vispārīgie vienādojumi

Parabolas vispārīgais vienādojums ir,

y = 4a(x – h) ² + k

(vai)

x = 4a(y – k) ² + h

Kur (h, k) ir parabolas virsotne.

Parabolas standarta vienādojumi

Parabolas standarta vienādojums ir,

y = cirvis ² + bx + c

(vai)

x = ir ² + ar + c

kur a nekad nevar būt nulle.

Parabolas daļas

Daži svarīgi parabolas termini un daļas ir:

• Fokuss: Fokuss ir parabolas fiksētais punkts.

• Virziens: Parabolas virziens ir taisne, kas ir perpendikulāra parabolas asij.

• Fokālais akords: Akordu, kas iet cauri parabolas fokusam, sagriežot parabolu divos atšķirīgos punktos, sauc par fokusa akordu.

• Fokālais attālums: Fokusa attālums ir attālums līdz punktam (x₁, un₁) uz parabolas no fokusa.

• Labā puse: Latus rectum ir fokusa akords, kas iet cauri parabolas fokusam un ir perpendikulārs parabolas asij. Latus taisnās zarnas garums ir LL’ = 4a.

• Ekscentriskums: Attiecību starp punkta attālumu no fokusa un tā attālumu no virziena sauc par ekscentriskumu (e). Parabolai ekscentricitāte ir vienāda ar 1, t.i., e = 1.

Parabolai ir četri standarta vienādojumi, kuru pamatā ir parabolas un tās ass orientācija. Katrai parabolai ir atšķirīga šķērsass un konjugētā ass.

Parabolas vienādojums	Parabola	Parabolas parametru formulas
un 2 = 4ax	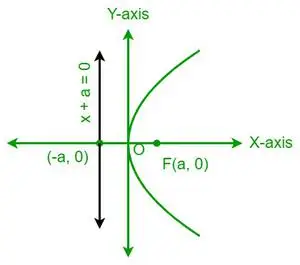Horizontālā parabola	Virsotne = (0,0) Fokuss = (a, 0) Parabola atveras uz labo pusi. Asu vienādojums ir y = 0 Virziena vienādojums ir x + a = 0 Latus taisnās zarnas garums = 4a
un 2 = -4ax	Horizontālā parabola	Virsotne = (0,0) Fokuss = (-a, 0) Parabola atveras uz kreiso pusi. Asu vienādojums ir y = 0 Virziena vienādojums ir x – a = 0 Latus taisnās zarnas garums = 4a
x 2 = 4ay	Vertikālā parabola	Virsotne = (0,0) Fokuss = (0, a) Parabola atveras uz augšu. Asu vienādojums ir x = 0 Virziena vienādojums ir y + a = 0 Latus taisnās zarnas garums = 4a
x 2 = -4ay	Vertikālā parabola	Virsotne = (0,0) Fokuss = (0, -a) Parabola atveras uz leju. Asu vienādojums ir x = 0 Virziena vienādojums ir y – a = 0 Latus taisnās zarnas garums = 4a

Šie ir novērojumi, kas veikti no parabolas vienādojumu standarta formas:

• Parabola ir simetriska pret savu asi. Piemēram, y²= 4ax ir simetriska pret x asi, bet x²= 4ay ir simetrisks attiecībā pret y asi.

• Ja parabola ir simetriska ap x asi, tad parabola atveras pa labi, ja x koeficients ir pozitīvs, un pa kreisi, ja x koeficients ir negatīvs.

• Ja parabola ir simetriska pret y asi, tad parabola atveras uz augšu, ja y koeficients ir pozitīvs, un uz leju, ja y koeficients ir negatīvs.

Tālāk ir norādīti parabolas standarta vienādojumi, kad simetrijas ass ir paralēla x asij vai y asij un virsotne neatrodas sākuma punktā.

Parabolas vienādojums	Parabola	Parabolas parametru formulas
(un – k)2= 4a(x–h)	Horizontālā parabola	Virsotne = (h, k) Fokuss = (h + a, k) Parabola atveras uz labo pusi. Asu vienādojums ir y = k Virziena vienādojums ir x = h – a Latus taisnās zarnas garums = 4a
(un – k)2= -4a(x - h)	Horizontālā parabola	Virsotne = (h, k) Fokuss = (h – a, k) Parabola atveras uz kreiso pusi. Asu vienādojums ir y = k Virziena vienādojums ir x = h + a Latus taisnās zarnas garums = 4a
(x–h)2= 4a(y–k)	Vertikālā parabola	Virsotne = (h, k) Fokuss = (h, k + a) Parabola atveras uz augšu. Ass vienādojums ir x = h Virziena vienādojums ir y = k – a Latus taisnās zarnas garums = 4a
(x–h)2= -4a(y - k)	Vertikālā parabola	Virsotne = (h, k) Fokuss = (h, k – a) Parabola atveras uz leju. Ass vienādojums ir x = h Virziena vienādojums ir y = k + a Latus taisnās zarnas garums = 4a

Parabolas atvasināšanas vienādojums

Lai P ir parabolas punkts, kura koordinātas ir (x, y). No parabolas definīcijas punkta P attālums līdz fokusam (F) ir vienāds ar tā paša punkta P attālumu līdz parabolas virzienam. Tagad apskatīsim virziena punktu X, kura koordinātas ir (-a, y).

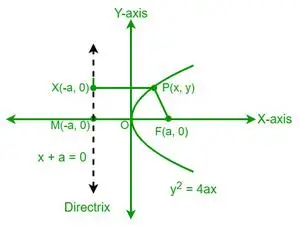
No parabolas ekscentricitātes definīcijas mums ir

e = PF/PX = 1

⇒ PF = PX

Fokusa koordinātas ir (a, 0). Tagad, izmantojot koordinātu attāluma formulu, mēs varam atrast punkta P (x, y) attālumu līdz fokusam F (a, 0).

PF = √[(x – a)²+ (un – 0)²]

⇒ PF = √[(x – a)²+ un²] ------ (1)

Virziena vienādojums ir x + a = 0. Lai atrastu PX attālumu, mēs izmantojam perpendikulārā attāluma formulu.

PX = (x + a)/√[1²+0²]

⇒ PX = x +a —————— (2)

Mēs jau zinām, ka PF = PX. Tātad, vienādojiet (1) un (2) vienādojumus.

√[(x – a)²+ un²] = (x + a)

No abām pusēm sadalot kvadrātā, mēs iegūstam,

⇒ [(x – a)²+ un²] = (x + a)²

⇒ x²+ a²– 2ax + y²= x²+ a²+ 2ax

⇒ un²– 2ax = 2ax

⇒ un²= 2ax + 2ax ⇒ un ² = 4ax

Tādējādi mēs esam atvasinājuši parabolas vienādojumu. Līdzīgi mēs varam iegūt pārējo trīs parabolu standarta vienādojumus.

• un²= -4ax
• x²= 4ay
• x²= -4ay

un ² = 4ax, un ² = -4ax, x ² = 4ay un x ² = -4ay ir parabolas standarta vienādojumi.

Raksti, kas saistīti ar parabolu:

• Apļa vienādojums
• Elipses vienādojums
• Hiperbolas vienādojums
• Parabolas pielietojumi reālajā dzīvē

Parabolas vienādojuma piemēri

1. piemērs. Atrodiet taisnās zarnas taisnās zarnas garumu, fokusu un virsotni, ja parabolas vienādojums ir y ² = 12x.

Risinājums:

Ņemot vērā,

Parabolas vienādojums ir y²= 12x

Salīdzinot doto vienādojumu ar standarta formu y²= 4ax

4a = 12

⇒ a = 12/4 = 3

Mēs to zinām,

Parabolas labā puse = 4a = 4 (3) = 12

Tagad parabolas fokuss = (a, 0) = (3, 0)

Dotās parabolas virsotne = (0, 0)

2. piemērs. Atrodiet parabolas vienādojumu, kas ir simetrisks pret X asi un iet caur punktu (-4, 5).

Risinājums:

Ņemot vērā,

Parabola ir simetriska pret X asi, un tās virsotne ir sākuma punktā.

Tādējādi vienādojumam var būt y forma²= 4ax vai y²= -4ax, kur zīme ir atkarīga no tā, vai parabola atveras uz kreiso vai labo pusi.

Parabolai ir jāatveras pa kreisi, jo tā iet cauri (-4, 5), kas atrodas otrajā kvadrantā.

Tātad vienādojums būs: y²= -4ax

Aizstājot (-4, 5) iepriekš minētajā vienādojumā,

⇒ (5)²= -4a(-4)

⇒ 25 = 16a

⇒ a = 25/16

Tāpēc parabolas vienādojums ir: y²= -4(25/16)x (vai) 4 g²= -25x.

3. piemērs. Atrodiet parabolas x fokusa, ass, virziena vienādojumu un taisnās zarnas taisnās zarnas koordinātas. ² = 16 gadi.

Risinājums:

Ņemot vērā,

Parabolas vienādojums ir: x²= 16 gadi

Salīdzinot doto vienādojumu ar standarta formu x²= 4ay,

4a = 16 ⇒ a = 4

Koeficients y ir pozitīvs, tāpēc parabola atveras uz augšu.

Arī simetrijas ass atrodas gar pozitīvo Y asi.

Tāpēc

Parabolas fokuss ir (a, 0) = (4, 0).

Virziena vienādojums ir y = -a, t.i., y = -4 vai y + 4 = 0.

Latus taisnās zarnas garums = 4a = 4(4) = 16.

4. piemērs. Atrodiet taisnās zarnas taisnās zarnas garumu, fokusu un virsotni, ja parabolas vienādojums ir 2(x-2) ² + 16 = g.

Risinājums:

Ņemot vērā,

Parabolas vienādojums ir 2(x-2)²+ 16 = un

Salīdzinot doto vienādojumu ar vispārējo parabolas vienādojumu y = a(x – h)²+ k, mēs saņemam

a = 2

(h, k) = (2, 16)

Mēs to zinām,

Parabolas taisnās zarnas garums = 4a

= 4(2) = 8

Tagad fokuss = (a, 0) = (2, 0)

Tagad virsotne = (2, 16)

5. piemērs. Parabolas vienādojums ir x ² – 12x + 4y – 24 = 0, pēc tam atrodiet tās virsotni, fokusu un virzienu.

Risinājums:

Ņemot vērā,

Parabolas vienādojums ir x²– 12x + 4g – 24 = 0

⇒ x²– 12x + 36 – 36 + 4 g – 24 = 0

⇒ (x–6)²+ 4 g – 60 = 0

⇒ (x–6)²= -4 (y + 15)

Iegūtais vienādojums ir formā (x – h)²= -4a(y - k)

-4a = -4 ⇒ a = 1

Tātad, virsotne = (h, k) = (6, – 15)

Fokuss = (h, k – a) = (6, -15-1) = (6, -16)

Virziena vienādojums ir y = k + a

⇒ y = -15 + 1 ⇒ y = -14

⇒ y + 14 = 0

Bieži uzdotie jautājumi par parabolas vienādojumu

Kā atrast parabolas standarta vienādojumu?

Parabolas standarta forma ir y²= 4ax vai x²= 4ay.

Kāds ir parastais parabolas vienādojums?

Parabolas y normālvienādojums²= 4ax ar slīpumu m ir norādīts šādi: y = mx – 2:00 – am ³

Kā atrast parabolas virsotni?

Dotajai parabolai: y = ax²+ bx + c tās virsotni var atrast, izmantojot formulu x = − b/2a. Pievienojiet šo x vērtību atpakaļ vienādojumam, lai atrastu atbilstošo y koordinātu.

kā lietot mysql darbagaldu