Kvadrātsakne no 3 ir pozitīvs reālais skaitlis, kas, reizinot ar sevi, dos skaitli 3. Kvadrātsakne no 3 ir iracionāls skaitlis, jo tas ir nebeidzams un neatkārtojams decimālskaitlis. Kvadrātsakne no 3 tiek apzīmēta kā √3 vai 31/2. Tā kā kvadrāts 3 ir iracionāls skaitlis, tā precīza decimālvērtība nekad netiek aprēķināta.
Kvadrātsaknes vērtība no 3, √3 = 1,732 (saīsināta)
Šajā rakstā mēs detalizēti uzzināsim par kvadrātsakni no 3.
Satura rādītājs
- Kas ir kvadrātsakne no 3?
- 3. saknes vērtība matemātikā
- Vai kvadrātsakne no 3 ir racionāla vai neracionāla?
- Kā atrast kvadrātsakni no 3?
- Skaitļa kvadrātsaknes īpašības
- Kvadrātsaknes tabula
Kas ir kvadrātsakne no 3?
Skaitļa kvadrātsakne ir skaitlis, kuru reizinot ar sevi, tiek iegūts sākotnējais skaitlis.
Piemērs: Kvadrātsakne no 16 ir 4, jo 4 × 4 = 16 tātad √16 = 4
java slēdža paziņojums
Kvadrātsakne no 3 vai vienkārši saukta par sakni 3 ir iracionāls skaitlis, kas, reizinot ar sevi, iegūst skaitli 3. Mēs varam norādīt saknes 3 aptuveno vērtību kā:
- Decimāldaļa: 1,732
- Eksponenta forma: 31/2
- Radikālā forma: √3
3. saknes vērtība matemātikā
Matemātikā jebkura skaitļa kvadrātsaknes atrašana ir ļoti svarīga, ideālā kvadrāta kvadrātsakni var viegli aprēķināt. Nepilnīgiem kvadrātiem ir grūti atrast kvadrātsakni, un to parasti aprēķina, izmantojot garās dalīšanas metodi.
3 sakne ir izteikta kā √3, tas ir neracionāls skaitlis, tāpēc tā decimālvērtību nekad nevar aprēķināt. Tas tiek attēlots radikālā formā kā (3)½. Kvadrātsakne no 3, kas noapaļota līdz 7 zīmēm aiz komata, ir 1,7320508.
Kvadrātsakne no 3 = 1,7320508075688772…
Vai kvadrātsakne no 3 ir racionāla vai neracionāla?
Kvadrātsakne 3 ir nebeidzama un neatkārtota decimāldaļa, un visas decimāldaļas un neatkārtojas decimāldaļskaitļi attiecas uz neracionālajiem skaitļiem. Tāpēc var droši teikt, ka √3 ir an neracionāls skaitlis .
java kamēr nosacījums
Kvadrātsaknes no 3 decimālais izvērsums ir,
√3 = 1,7320508075688772…
Tā kā tas neatkārtojas un nebeidzas, mēs droši varam teikt, ka √3 ir neracionāls.
Kā atrast kvadrātsakni no 3?
Vienmēr ir vieglāk aprēķināt perfekto kvadrātu kvadrātsakni, bet, lai aprēķinātu kvadrātsakni neperfektam kvadrātam, mums ir jāveic garās dalīšanas metode.
Lai aprēķinātu kvadrātsakni no 3, mums ir jāveic tālāk norādītās darbības.
1. darbība: Ierakstiet 3 kā 3,000000 (kur nulles vienmēr tiek turētas pāru veidā), lai būtu vieglāk sadalīt.
2. darbība: Tagad meklējiet ideālo kvadrātu, kas ir mazāks par 3, t.i., 1, un sadaliet skaitli ar to.
foreach mašīnrakstā
3. darbība: Tagad koeficients ir 1, bet atlikums ir 2. Mēs ievietosim koeficientā decimāldaļu un pazemināsim nulles pāri tālākai dalīšanai.
4. darbība: Tagad nākamā dividende ir 200 un nākamais dalītājs būs 2X (koeficients 1 tiek pievienots iepriekšējam dalītājam 1 un X ir desmitajā vietā), lai skaitļa 2X un X reizinājumam būtu jābūt mazākam par 200. nākamā vērtība 27 kā jaunais dalītājs.
5. darbība: Tagad koeficientam aiz komata tiek pievienots 7, tātad koeficienta vērtība būs 1,7 un jaunais dalītājs tiks iegūts, saskaitot 7 pret 27, tātad 34Y, kur Y atrodas simtajā vietā. Izmantojot iepriekšējās darbības, mēs varam turpināt un iegūt kvadrātsakni no 3 koeficientā.
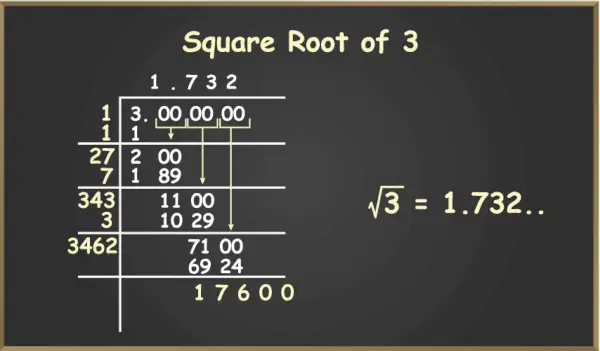
Kvadrātsakne no 3
Tagad samaziniet nākamo nulles pāri un atkārtojiet 4. un 5. darbību. To var izdarīt bezgalīgiem soļiem, jo precīza kvadrātsaknes vērtība no 2 palielinās līdz bezgalīgām zīmēm aiz komata. Mēs varam aprēķināt rezultātu līdz 4 zīmēm aiz komata, jo to var izmantot apm. kvadrātsaknes vērtība.
Skaitļa kvadrātsaknes īpašības
Tālāk ir apskatītas dažādas skaitļa kvadrātsaknes īpašības,
- Perfektiem kvadrātskaitļiem ir ideālas kvadrātsaknes.
- Kvadrātsakne no pat perfekta kvadrāta ir pāra.
- Kvadrātsakne no nepāra perfekta kvadrāta ir nepāra.
- Negatīvā skaitļa kvadrātsakne ir a kompleksais skaitlis .
Kvadrātsaknes tabula
Matemātikā plaši tiek izmantotas dažādu skaitļu kvadrātsaknes. Tālāk sniegtajā tabulā ir norādīta dažādu parasti izmantoto skaitļu kvadrātsakne.
| Numurs | Kvadrātsakne |
|---|---|
| 1 | √(1) = 1 |
| 2 | √(2) = 1,414 (aptuveni) |
| 3 | √(3) = 1,732 (aptuveni) |
| 4 | √(4) = 2 |
| 5 | √(5) = 2,236 (aptuveni) |
| 9 | √(9) = 3 |
| 16 | √(16) = 4 |
| 25 | √(25) = 5 |
Tāpat pārbaudiet
- Kvadrātsakne no 2
- Reālie skaitļi
- Racionālie skaitļi
Bieži uzdotie jautājumi par kvadrātsakni no 3
Kāda ir 3 kvadrātsaknes vērtība?
Aptuvenā kvadrātsaknes vērtība no 3 ir 1,73205.
Alise Manjonoka
Kāpēc kvadrātsakne no 3 ir neracionāls skaitlis?
Kvadrātsaknes 3 vērtība ir decimāldaļa, kas neatkārtojas un nebeidzas, tāpēc tas ir neracionāls skaitlis.
Vai skaitlis 3 ir ideāls kvadrāts?
3 ir pirmskaitlis, un pirmskaitļiem nav citu faktoru kā 1 un pašiem. Tādējādi mēs varam teikt, ka 3 nav ideāls kvadrāts.
Kā mēs varam atrast √3 vērtību?
Vērtību √3 var atrast, izmantojot garās dalīšanas metodi. Tā kā 3 nav ideāls kvadrāts, tā precīza vērtība nekad nav atrasta.
Kāda ir saknes 2 vērtība?
2. sakne ir neracionāls skaitlis, tāpēc tā precīza decimālvērtība nekad netiek atrasta. Aptuvenā saknes 2 vērtība ir, √2 = 1,414 (aptuveni)
