Sin Cos formulas trigonometrijā: Trigonometrija, kā norāda tās nosaukums, ir trīsstūru izpēte. Tā ir svarīga matemātikas nozare, kas pēta attiecības starp taisnleņķa trijstūra malu garumiem un leņķiem, kā arī palīdz noteikt trūkstošos trijstūra malu garumus vai leņķus. Ir sešas trigonometriskās attiecības vai funkcijas: sinusa, kosinuss, tangenss, kosekants, sekants un kotangenss, kur kosekants, sekants un kotangenss ir pārējo trīs funkciju, t.i., attiecīgi sinusa, kosinusa un tangensa, abpusējas funkcijas.
Trigonometriskā attiecība tiek definēta kā taisnleņķa trijstūra malu garumu attiecība. Trigonometrija mūsu ikdienas dzīvē tiek izmantota dažādās jomās. Tas palīdz noteikt pauguru vai ēku augstumu. To izmanto arī tādās jomās kā kriminoloģija, būvniecība, fizika, arheoloģija, kuģu dzinēju inženierija utt.
Šajā rakstā mēs izpētīsim visu trigonometrijas formulas galvenokārt sin un cos formulas ar to piemēriem, kā arī visu trigonometrijas formulu saraksts.
Satura rādītājs
- Formulas trigonometrijā
- Dažas Sin Cos pamata formulas
- Sin Cos formulu tabula
- Sin Cos formulu piemēri
- Prakses problēmas par Sin Cos formulām trigonometrijā ar piemēriem
Formulas trigonometrijā
Apskatīsim taisnleņķa trīsstūri XYZ, kur ∠Y = 90°. Lai leņķis virsotnē Z ir θ. Malu, kas atrodas blakus θ, sauc par blakus malu, un malu, kas ir pretēja θ, sauc par pretējo pusi. Hipotenūza ir mala, kas ir pretēja taisnajam leņķim vai taisnā leņķa garākā mala.
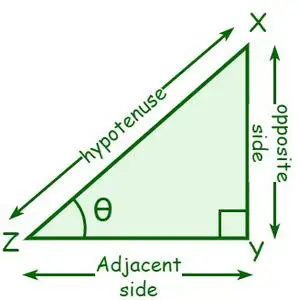
- sin θ = pretējā puse/hipotenūza
- cos θ = Blakus puse/Hipotenūza
- iedegums θ = pretējā puse/blakuspuse
- cosec θ = 1/sin θ = hipotenūza/pretējā puse
- sec θ = 1/ cos θ = Hipotenūza/Blakuspuse
- gultiņa θ = 1/ iedegums θ = blakus puse/pretējā puse
Sinusa formula
Leņķa sinuss taisnleņķa trijstūrī ir pretējās malas garuma attiecība pret hipotenūzas garumu pret doto leņķi. Sinusa funkcija tiek attēlota kā grēks.
sin θ = pretējā puse/hipotenūza
Kosinusa formula
Leņķa kosinuss taisnleņķa trijstūrī ir blakus esošās malas garuma attiecība pret hipotenūzas garumu pret doto leņķi. Kosinusa funkcija tiek attēlota kā cos.
burbuļu kārtošana algoritmācos θ = Blakus puse/Hipotenūza
Dažas Sin Cos pamata formulas
Sinusa un kosinusa funkcijas kvadrantos
- Sinusa funkcija ir pozitīva pirmajā un otrajā kvadrantā un negatīva trešajā un ceturtajā kvadrantā.
- Kosinusa funkcija ir pozitīva pirmajā un ceturtajā kvadrantā un negatīva otrajā un trešajā kvadrantā.
Grādi
Kvadrants
Sinusa funkcijas zīme
Kosinusa funkcijas zīme
0° līdz 90°
1. kvadrants
+ (pozitīvs)
+ (pozitīvs)
90° līdz 180°
2. kvadrants
+ (pozitīvs)
– (negatīvs)
180° līdz 270°
3. kvadrants
– (negatīvs)
– (negatīvs)
270° līdz 360°
4. kvadrants
– (negatīvs)
+ (pozitīvs)
Sinusa un kosinusa funkciju negatīvā leņķa identitāte
- Negatīvā leņķa sinuss vienmēr ir vienāds ar leņķa negatīvo sinusu.
sin (– θ) = – grēks θ
- Negatīvā leņķa kosinuss vienmēr ir vienāds ar leņķa kosinusu.
cos (– θ) = cos θ
Saistība starp sinusu un kosinusu funkciju
sin θ = cos (90° – θ)
Sinusa un kosinusa funkciju savstarpējās funkcijas
- Kosekanta funkcija ir sinusa funkcijas abpusēja funkcija.
cosec θ = 1/sin θ
- Sekanta funkcija ir kosinusa funkcijas abpusēja funkcija.
sec θ = 1/cos θ
Pitagora identitāte
bez 2 θ + cos 2 θ = 1
Sinusa un kosinusa funkciju periodiskas identitātes
sin (θ + 2nπ) = grēks θ
cos (θ + 2nπ) = cos θ
Double Angle formulas sinusa un kosinusa funkcijām
sin 2θ = 2 sin θ cos θ
cos 2θ = cos 2 θ – grēks 2 θ = 2 cos 2 θ – 1 = 1 – 2 grēks 2 i
Pusleņķa identitātes sinusa un kosinusa funkcijām
sin (θ/2) = ±√[(1 – cos θ)/2]
cos (θ/2) = ±√[(1 + cos θ)/2]
Trīskāršās leņķa identitātes sinusa un kosinusa funkcijām
sin 3θ = 3 sin θ – 4 sin 3 i
cos 3θ = 4cos 3 θ – 3 cos θ
Summu un starpības formulas
- Sinusa funkcija
grēks (A + B) = grēks A cos B + cos A grēks B
sin (A – B) = grēks A cos B – cos A grēks B
- Kosinusa funkcija
cos (A + B) = cos A cos B – sin A sin B
cos (A – B) = cos A cos B + sin A sin B
Sinusu likums jeb sinusa likums
Sinusa likuma sinusu likums ir trigonometrisks likums, kas nosaka attiecību starp trijstūra malu garumiem un leņķiem.

a/sin A = b/sin B = c/sin C
Kur a, b un c ir trīsstūra ABC trīs malu garumi, bet A, B un C ir leņķi.
Kosinusu likums
Kosinusa likuma kosinusu likumu izmanto, lai noteiktu trūkstošos vai nezināmos trijstūra leņķus vai malu garumus.

a 2 = b 2 + c 2 – 2bc cos A
b 2 = c 2 + a 2 – 2ca cos B
c 2 = a 2 + b 2 – 2ab cos C
Kur a, b un c ir trīsstūra ABC trīs malu garumi, bet A, B un C ir leņķi.
Sin Cos formulu tabula
Šeit ir Sin un Cos formulu tabula/ saraksts dažādiem leņķiem grādos un radiānos:
Sin Cos formulu saraksts
| Leņķis (grādos) | Leņķis (radiānos) | grēks i | cos θ |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | p/6 | 1/2 | _3/2 |
| 45° | p/4 | 1/√2 | 1/√2 |
| 60° | p/3 | √3/2 | 1/2 |
| 90° | p/2 | 1 | 0 |
| 120° | 2p/3 | √3/2 | -1/2 |
| 150° | 5p/6 | 1/2 | -√3/2 |
| 180° | Pi | 0 | -1 |
Sin Cos formulu piemēri
1. uzdevums: ja cos α = 24/25, tad atrodiet sin α vērtību.
Risinājums:
Ņemot vērā,
cos α = 24/25
No Pitagora identitātēm, kas mums ir;
cos2θ + grēks2θ = 1
(24/25)2+ bez2α = 1
bez2α = 1 – (24/25)2
bez2α = 1 – (576/625) = (625 – 576)/625
bez2α = (625–576)/625 = 49/626
sin α = √49/625 = ±7/25
Tādējādi grēks α = ±7/25.
2. uzdevums: pierādi sin 2A un cos 2A formulas, ja ∠A= 30°.
Risinājums:
Dots, ∠A= 30°
Mēs to zinām,
1) sin 2A = 2 sin A cos A
sin 2(30°) = 2 sin 30° cos 30°
sin 60° = 2 × (1/2) × (√3/2) {Tā kā grēks 30° = 1/2, cos 30° = √3/2 un sin 60° = √3/2}
√3/2 = √3/2
L.H.S = R.H.S
2) cos 2A = 2cos2A-1
cos 2(30°) = 2cos2(30°) – 1
cos 60° = 2 (√3/2)2– 1 = 3/2 – 1 {Tā kā cos 60° = 1/2 un cos 30° = √3/2}
1/2 = 1/2
L.H.S = R.H.S
Līdz ar to pierādīts.
3. uzdevums: atrodiet cos x vērtību, ja tan x = 3/4.
Risinājums:
Ņemot vērā, iedegums x = 3/4
Mēs to zinām,
iedegums x = pretējā puse/blakuspuse = 3/4
Lai atrastu hipotenūzu, mēs izmantojam Pitagora teorēmu:
hipotenūza2= pretējs2+ blakus2
H2= 32+ 42
H2= 9 + 16 = 25
H = √25 = 5
Tagad cos x = blakus esošā puse/hipotenūza
cos x = 4/5
Tādējādi cos x vērtība ir 4/5.
4. problēma: atrodiet ∠C (grādos) un ∠A (grādos), ja ∠B = 45°, BC = 15 collas un AC = 12 collas.

Risinājums:
Dots: ∠B = 45°, BC = a = 15 collas un AC = b = 12 collas.
No sinusa likuma mums ir
a/sin A = b/sin B = c/sin C
⇒ a/sin A = b/sin B
⇒ 15/sin A = 12/sin 45°
⇒ 15/sin A = 12/(1/√2)
⇒ 15/sin A = 12√2 = 16,97
⇒ bez A = 15/16,97 = 0,8839
⇒ ∠A = grēks-1(0,8839) = 62,11°
Mēs zinām, ka trijstūra iekšējo leņķu summa ir 180°.
Tātad ∠A + ∠B + ∠C = 180°
⇒ 62,11° + 45° + ∠C = 180°
⇒ ∠C = 180° – (62,11° + 45°) = 72,89°
Tādējādi ∠A = 62,11° un ∠C = 72,89°.
5. uzdevums. Pierādiet kosinusa funkcijas pusleņķa identitātes.
Risinājums:
Kosinusa funkcijas pusleņķa identitāte ir:
cos (θ/2) = ±√[(1 + cos θ)/2]
No dubultā leņķa identitātēm mums ir,
cos 2A = 2 cos2A-1
Tagad nomainiet A ar θ/2 abās pusēs
⇒ cos 2(θ/2) = 2 cos2(i/2) – 1
⇒ cos θ = 2 cos2(i/2) – 1
⇒ 2cos2(θ/2) = cos θ + 1
⇒ cos2(θ/2) = (cos θ + 1)/2
⇒ cos (θ/2) = ±√[(1 + cos θ)/2]
Līdz ar to pierādīts.
Prakses problēmas par Sin Cos formulām trigonometrijā ar piemēriem
1. Dots sin θ = 3/5. Atrodiet cos θ.
2. Pierādiet identitāti sin(2A) = 2 sinA cosA, ja A=45∘.
3. Ja cos α = 5/13. Atrodi grēku(2a).
4. Atrisiniet θ, ja sin θ = cos(90∘−θ).
5. Ja tan β = 2. Izmantojot Pitagora identitāti, atrodiet sin β un cos β.
Bieži uzdotie jautājumi par Sin Cos formulām trigonometrijā ar piemēriem
Kādas ir trigonometrijas sinusa un kosinusa pamatformulas?
Galvenās sinusa un kosinusa formulas ir sin θ = Pretstats/Hipotenūza un cos θ = Blakus/Hipotenūza, kur θ ir leņķis taisnleņķa trijstūrī.
Kā atrast īpašu leņķu sinusu un kosinusu?
Īpašiem leņķiem, piemēram, 0∘, 30∘, 45∘, 60∘ un 90∘, ir noteiktas sinusa un kosinusa vērtības, kuras var atcerēties, izmantojot trigonometriskās tabulas vai vienību apļa jēdzienus.
Kāda ir saistība starp sinusa un kosinusa funkcijām?
Sinusa un kosinusa funkcijas ir saistītas ar identitāti sin θ = cos(90∘- θ) un Pitagora identitāte bez 2 θ+cos 2 θ = 1.
atlases kārtot java
Kā jūs izmantojat dubultā leņķa formulas sinususam un kosinusam?
Dubultā leņķa formulas ir sin(2θ) = 2sinθcosθ un cos(2θ)=cos 2 θ – grēks 2 i. Tos izmanto, lai izteiktu dubultleņķu trigonometriskās funkcijas atsevišķu leņķu izteiksmē.
Kā jūs varat atrast sinusa un kosinusa vērtības leņķiem dažādos kvadrantos?
Sinusa un kosinusa funkciju zīmes ir atkarīgas no kvadranta, kurā atrodas leņķis:
- Pirmais kvadrants: sin θ> 0 un cos θ> 0
- Otrais kvadrants: sin θ> 0 un cos θ < 0
- Trešais kvadrants: sinθ <0 un cosθ < 0
- Ceturtais kvadrants: sinθ 0
