 #practiceLinkDiv { display: none !important; }
#practiceLinkDiv { display: none !important; }Reversās dzēšanas algoritms ir cieši saistīts ar Kruskala algoritms . Kruskal algoritmā mēs darām: kārtojam malas, palielinot to svaru secību. Pēc šķirošanas mēs pa vienam paņemam malas augošā secībā. Mēs iekļaujam pašreizējo atlasīto malu, ja, iekļaujot to aptverošajā kokā, neveido nekādu ciklu, kamēr nav V-1 malas, kur V = virsotņu skaits.
Apgrieztās dzēšanas algoritmā mēs kārtojam visas malas samazinās to svaru secība. Pēc šķirošanas mēs pa vienam noņemam malas dilstošā secībā. Mēs iekļaut pašreizējo izvēlēto malu, ja pašreizējās malas izslēgšana izraisa atvienojumu pašreizējā grafikā . Galvenā ideja ir dzēst malu, ja tās dzēšana neizraisa grafa atvienošanu.
python inicializācijas saraksts
Algoritms:
- Kārtot visas grafika malas malu svara nepalielinošā secībā.
- Inicializējiet MST kā sākotnējo grafiku un noņemiet papildu malas, izmantojot 3. darbību.
- Izvēlieties augstāko svara malu no atlikušajām malām un pārbaudiet, vai, dzēšot malu, grafiks tiek atvienots vai nē .
Ja atvieno, mēs neizdzēšam malu.
Citādi izdzēšam malu un turpinām.
Ilustrācija:
Ļaujiet mums saprast, izmantojot šādu piemēru:
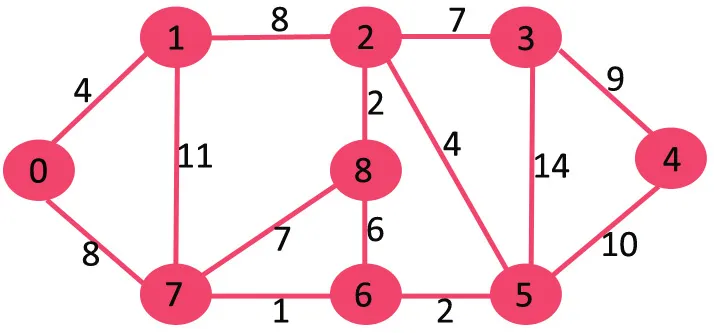
Ja izdzēšam 14. svara lielākās malas, grafiks netiek atvienots, tāpēc mēs to noņemam.
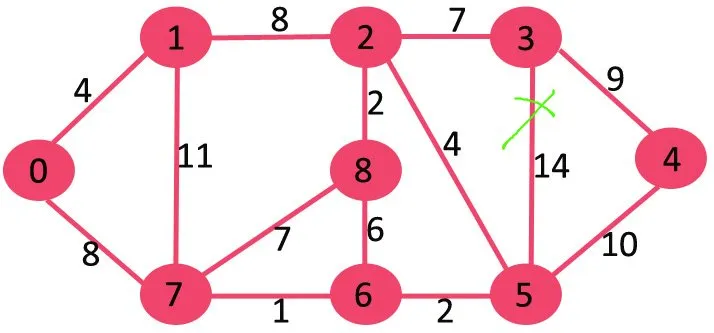
Pēc tam mēs izdzēšam 11, jo tā dzēšana neatvieno grafiku.
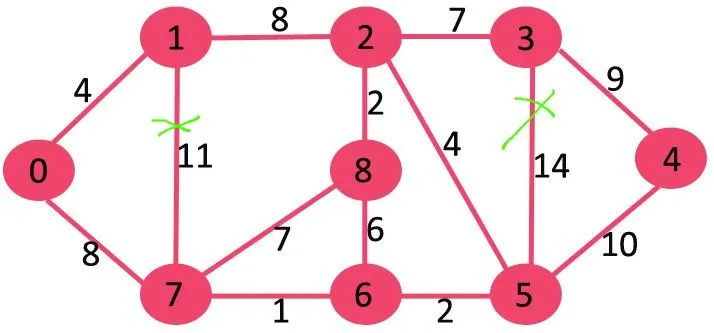
Pēc tam mēs izdzēšam 10, jo to dzēšana neatvieno grafiku.

Nākamais ir 9. Mēs nevaram izdzēst 9, jo tā dzēšana izraisa atvienošanu.
nav ieejas signāla

Mēs turpinām šo ceļu, un nākamās malas paliek pēdējā MST.
Edges in MST
(3 4)
(0 7)
(2 3)
(2 5)
(0 1)
(5 6)
(2 8)
(6 7)
Piezīme: Vienāda svara malu gadījumā varam izvēlēties jebkuru viena un tā paša svara malu malu.
Ieteicamā prakse Reversās dzēšanas algoritms minimālajam aptverošajam kokam Izmēģiniet to!Īstenošana:
C++// C++ program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm #include
// Java program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm import java.util.*; // class to represent an edge class Edge implements Comparable<Edge> { int u v w; Edge(int u int v int w) { this.u = u; this.w = w; this.v = v; } public int compareTo(Edge other) { return (this.w - other.w); } } // Class to represent a graph using adjacency list // representation public class GFG { private int V; // No. of vertices private List<Integer>[] adj; private List<Edge> edges; @SuppressWarnings({ 'unchecked' 'deprecated' }) public GFG(int v) // Constructor { V = v; adj = new ArrayList[v]; for (int i = 0; i < v; i++) adj[i] = new ArrayList<Integer>(); edges = new ArrayList<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].add(v); // Add w to v’s list. adj[v].add(u); // Add w to v’s list. edges.add(new Edge(u v w)); } // function to perform dfs private void DFS(int v boolean[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex for (int i : adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private boolean IsConnected() { boolean[] visited = new boolean[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost Collections.sort(edges); int mst_wt = 0; // Initialize weight of MST System.out.println('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.size() - 1; i >= 0; i--) { int u = edges.get(i).u; int v = edges.get(i).v; // Remove edge from undirected graph adj[u].remove(adj[u].indexOf(v)); adj[v].remove(adj[v].indexOf(u)); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].add(v); adj[v].add(u); // This edge is part of MST System.out.println('(' + u + ' ' + v + ')'); mst_wt += edges.get(i).w; } } System.out.println('Total weight of MST is ' + mst_wt); } // Driver code public static void main(String[] args) { // create the graph given in above figure int V = 9; GFG g = new GFG(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by Prithi_Dey
# Python3 program to find Minimum Spanning Tree # of a graph using Reverse Delete Algorithm # Graph class represents a directed graph # using adjacency list representation class Graph: def __init__(self v): # No. of vertices self.v = v self.adj = [0] * v self.edges = [] for i in range(v): self.adj[i] = [] # function to add an edge to graph def addEdge(self u: int v: int w: int): self.adj[u].append(v) # Add w to v’s list. self.adj[v].append(u) # Add w to v’s list. self.edges.append((w (u v))) def dfs(self v: int visited: list): # Mark the current node as visited and print it visited[v] = True # Recur for all the vertices adjacent to # this vertex for i in self.adj[v]: if not visited[i]: self.dfs(i visited) # Returns true if graph is connected # Returns true if given graph is connected else false def connected(self): visited = [False] * self.v # Find all reachable vertices from first vertex self.dfs(0 visited) # If set of reachable vertices includes all # return true. for i in range(1 self.v): if not visited[i]: return False return True # This function assumes that edge (u v) # exists in graph or not def reverseDeleteMST(self): # Sort edges in increasing order on basis of cost self.edges.sort(key = lambda a: a[0]) mst_wt = 0 # Initialize weight of MST print('Edges in MST') # Iterate through all sorted edges in # decreasing order of weights for i in range(len(self.edges) - 1 -1 -1): u = self.edges[i][1][0] v = self.edges[i][1][1] # Remove edge from undirected graph self.adj[u].remove(v) self.adj[v].remove(u) # Adding the edge back if removing it # causes disconnection. In this case this # edge becomes part of MST. if self.connected() == False: self.adj[u].append(v) self.adj[v].append(u) # This edge is part of MST print('( %d %d )' % (u v)) mst_wt += self.edges[i][0] print('Total weight of MST is' mst_wt) # Driver Code if __name__ == '__main__': # create the graph given in above figure V = 9 g = Graph(V) # making above shown graph g.addEdge(0 1 4) g.addEdge(0 7 8) g.addEdge(1 2 8) g.addEdge(1 7 11) g.addEdge(2 3 7) g.addEdge(2 8 2) g.addEdge(2 5 4) g.addEdge(3 4 9) g.addEdge(3 5 14) g.addEdge(4 5 10) g.addEdge(5 6 2) g.addEdge(6 7 1) g.addEdge(6 8 6) g.addEdge(7 8 7) g.reverseDeleteMST() # This code is contributed by # sanjeev2552
// C# program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm using System; using System.Collections.Generic; // class to represent an edge public class Edge : IComparable<Edge> { public int u v w; public Edge(int u int v int w) { this.u = u; this.v = v; this.w = w; } public int CompareTo(Edge other) { return this.w.CompareTo(other.w); } } // Graph class represents a directed graph // using adjacency list representation public class Graph { private int V; // No. of vertices private List<int>[] adj; private List<Edge> edges; public Graph(int v) // Constructor { V = v; adj = new List<int>[ v ]; for (int i = 0; i < v; i++) adj[i] = new List<int>(); edges = new List<Edge>(); } // function to Add an edge public void AddEdge(int u int v int w) { adj[u].Add(v); // Add w to v’s list. adj[v].Add(u); // Add w to v’s list. edges.Add(new Edge(u v w)); } // function to perform dfs private void DFS(int v bool[] visited) { // Mark the current node as visited and print it visited[v] = true; // Recur for all the vertices adjacent to // this vertex foreach(int i in adj[v]) { if (!visited[i]) DFS(i visited); } } // Returns true if given graph is connected else false private bool IsConnected() { bool[] visited = new bool[V]; // Find all reachable vertices from first vertex DFS(0 visited); // If set of reachable vertices includes all // return true. for (int i = 1; i < V; i++) { if (visited[i] == false) return false; } return true; } // This function assumes that edge (u v) // exists in graph or not public void ReverseDeleteMST() { // Sort edges in increasing order on basis of cost edges.Sort(); int mst_wt = 0; // Initialize weight of MST Console.WriteLine('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (int i = edges.Count - 1; i >= 0; i--) { int u = edges[i].u; int v = edges[i].v; // Remove edge from undirected graph adj[u].Remove(v); adj[v].Remove(u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (IsConnected() == false) { adj[u].Add(v); adj[v].Add(u); // This edge is part of MST Console.WriteLine('({0} {1})' u v); mst_wt += edges[i].w; } } Console.WriteLine('Total weight of MST is {0}' mst_wt); } } class GFG { // Driver code static void Main(string[] args) { // create the graph given in above figure int V = 9; Graph g = new Graph(V); // making above shown graph g.AddEdge(0 1 4); g.AddEdge(0 7 8); g.AddEdge(1 2 8); g.AddEdge(1 7 11); g.AddEdge(2 3 7); g.AddEdge(2 8 2); g.AddEdge(2 5 4); g.AddEdge(3 4 9); g.AddEdge(3 5 14); g.AddEdge(4 5 10); g.AddEdge(5 6 2); g.AddEdge(6 7 1); g.AddEdge(6 8 6); g.AddEdge(7 8 7); g.ReverseDeleteMST(); } } // This code is contributed by cavi4762
// Javascript program to find Minimum Spanning Tree // of a graph using Reverse Delete Algorithm // Graph class represents a directed graph // using adjacency list representation class Graph { // Constructor constructor(V) { this.V = V; this.adj = []; this.edges = []; for (let i = 0; i < V; i++) { this.adj[i] = []; } } // function to add an edge to graph addEdge(u v w) { this.adj[u].push(v);// Add w to v’s list. this.adj[v].push(u);// Add w to v’s list. this.edges.push([w [u v]]); } DFS(v visited) { // Mark the current node as visited and print it visited[v] = true; for (const i of this.adj[v]) { if (!visited[i]) { this.DFS(i visited); } } } // Returns true if given graph is connected else false isConnected() { const visited = []; for (let i = 0; i < this.V; i++) { visited[i] = false; } // Find all reachable vertices from first vertex this.DFS(0 visited); // If set of reachable vertices includes all // return true. for (let i = 1; i < this.V; i++) { if (!visited[i]) { return false; } } return true; } // This function assumes that edge (u v) // exists in graph or not reverseDeleteMST() { // Sort edges in increasing order on basis of cost this.edges.sort((a b) => a[0] - b[0]); let mstWt = 0;// Initialize weight of MST console.log('Edges in MST'); // Iterate through all sorted edges in // decreasing order of weights for (let i = this.edges.length - 1; i >= 0; i--) { const [u v] = this.edges[i][1]; // Remove edge from undirected graph this.adj[u] = this.adj[u].filter(x => x !== v); this.adj[v] = this.adj[v].filter(x => x !== u); // Adding the edge back if removing it // causes disconnection. In this case this // edge becomes part of MST. if (!this.isConnected()) { this.adj[u].push(v); this.adj[v].push(u); // This edge is part of MST console.log(`(${u} ${v})`); mstWt += this.edges[i][0]; } } console.log(`Total weight of MST is ${mstWt}`); } } // Driver code function main() { // create the graph given in above figure var V = 9; var g = new Graph(V); // making above shown graph g.addEdge(0 1 4); g.addEdge(0 7 8); g.addEdge(1 2 8); g.addEdge(1 7 11); g.addEdge(2 3 7); g.addEdge(2 8 2); g.addEdge(2 5 4); g.addEdge(3 4 9); g.addEdge(3 5 14); g.addEdge(4 5 10); g.addEdge(5 6 2); g.addEdge(6 7 1); g.addEdge(6 8 6); g.addEdge(7 8 7); g.reverseDeleteMST(); } main();
Izvade
Edges in MST (3 4) (0 7) (2 3) (2 5) (0 1) (5 6) (2 8) (6 7) Total weight of MST is 37
Laika sarežģītība: O((E*(V+E)) + E log E) kur E ir malu skaits.
Telpas sarežģītība: O(V+E) kur V ir virsotņu skaits un E ir šķautņu skaits. Mēs izmantojam blakus esošo sarakstu, lai saglabātu grafiku, tāpēc mums ir nepieciešama vieta, kas ir proporcionāla O(V+E).
Piezīmes:
- Iepriekš minētā ieviešana ir vienkārša/naiva reversās dzēšanas algoritma ieviešana, un to var optimizēt uz O (E log V (log log V)3) [Avots: Nedēļa ]. Bet šī optimizētā laika sarežģītība joprojām ir mazāka par Prim un Kruskal MST algoritmi.
- Iepriekš minētā ieviešana maina sākotnējo grafiku. Mēs varam izveidot diagrammas kopiju, ja ir jāsaglabā sākotnējā diagramma.
Izveidojiet viktorīnu
