R-matrica ir divdimensiju datu izkārtojums rindās un kolonnās.
Matricā rindas ir tās, kas darbojas horizontāli, un kolonnas ir tās, kas darbojas vertikāli. In R programmēšana , matricas ir divdimensiju, viendabīgas datu struktūras. Šie ir daži matricu piemēri:
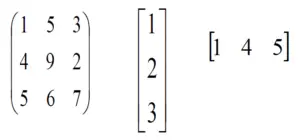
R – Matricas
Matricas izveide R
Lai izveidotu matricu R, jums jāizmanto funkcija, ko sauc matrica () .
Argumenti tam matrica () ir vektora elementu kopa. Jums ir jānorāda, cik rindu un cik kolonnu vēlaties iekļaut savā matricā.
Piezīme: Pēc noklusējuma matricas ir kolonnu secībā.
Sintakse, lai izveidotu R-matricu
matrica (dati, nrow, ncol, byrow, dimnames)
Parametri:
- dati - vērtības, kuras vēlaties ievadīt
- nrow - Nē. no rindām
- ncol - Nē. kolonnu
- blakus - loģisks pavediens, ja “patiesā” vērtība tiks piešķirta pēc rindām
- dimnames - rindu un kolonnu nosaukumi
Piemērs:
java struktūra
R
# R program to create a matrix> > A =>matrix>(> > ># Taking sequence of elements> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> > ># No of rows> >nrow = 3,> > ># No of columns> >ncol = 3,> > ># By default matrices are in column-wise order> ># So this parameter decides how to arrange the matrix> >byrow =>TRUE> )> > # Naming rows> rownames>(A) =>c>(>'a'>,>'b'>,>'c'>)> > # Naming columns> colnames>(A) =>c>(>'c'>,>'d'>,>'e'>)> > cat>(>'The 3x3 matrix:
'>)> print>(A)> |
>
>Izvade
The 3x3 matrix: c d e a 1 2 3 b 4 5 6 c 7 8 9>
Īpašu matricu izveide R
R ļauj izveidot dažādu veidu matricas, izmantojot argumentus, kas tiek nodoti funkcijai matrix().
1. Matrica, kurā visas rindas un kolonnas ir aizpildītas ar vienu konstanti “k”.
Lai izveidotu šādu R matricu, sintakse ir norādīta zemāk:
Sintakse: matrica(k, m, n)
Parametri:
k: konstante
m: rindu skaits
n: kolonnu skaits
Piemērs:
R
# R program to illustrate> # special matrices> # Matrix having 3 rows and 3 columns> # filled by a single constant 5> print>(>matrix>(5, 3, 3))> |
>
>Izvade
[,1] [,2] [,3] [1,] 5 5 5 [2,] 5 5 5 [3,] 5 5 5>
2. Diagonālā matrica:
Diagonālā matrica ir matrica, kurā visi ieraksti ārpus galvenās diagonāles ir nulle. Lai izveidotu šādu R matricu, sintakse ir norādīta zemāk:
Sintakse: diag(k, m, n)
Parametri:
k: konstantes/masīvs
m: rindu skaits
n: kolonnu skaits
Piemērs:
R
# R program to illustrate> # special matrices> # Diagonal matrix having 3 rows and 3 columns> # filled by array of elements (5, 3, 3)> print>(>diag>(>c>(5, 3, 3), 3, 3))> |
>
>Izvade
[,1] [,2] [,3] [1,] 5 0 0 [2,] 0 3 0 [3,] 0 0 3>
3. Identitātes matrica:
Identitātes matrica, kurā visi galvenās diagonāles elementi ir vieninieki un visi pārējie elementi ir nulles. Lai izveidotu šādu R matricu, sintakse ir norādīta zemāk:
Sintakse: diag(k, m, n)
Parametri:
k: 1
m: rindu skaits
n: kolonnu skaits
Piemērs:
R
# R program to illustrate> # special matrices> # Identity matrix having> # 3 rows and 3 columns> print>(>diag>(1, 3, 3))> |
c# datetime
>
>Izvade
[,1] [,2] [,3] [1,] 1 0 0 [2,] 0 1 0 [3,] 0 0 1>
4. Matricas metrika
Matricas metrika stāsta par jūsu izveidoto matricu. Iespējams, vēlēsities uzzināt rindu skaitu, kolonnu skaitu, matricas izmērus.
Tālāk sniegtais piemērs palīdzēs jums atbildēt uz šādiem jautājumiem:
- Kā jūs varat uzzināt matricas dimensiju?
- Kā jūs varat zināt, cik rindu ir matricā?
- Cik kolonnu ir matricā?
- Cik daudz elementu ir matricā?
Piemērs:
R
# R program to illustrate> # matrix metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> cat>(>'Dimension of the matrix:
'>)> print>(>dim>(A))> cat>(>'Number of rows:
'>)> print>(>nrow>(A))> cat>(>'Number of columns:
'>)> print>(>ncol>(A))> cat>(>'Number of elements:
'>)> print>(>length>(A))> # OR> print>(>prod>(>dim>(A)))> |
>
>Izvade
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 Dimension of the matrix: [1] 3 3 Number of rows: [1] 3 Number of columns: [1] 3 Number of elements: [1] ...>
Piekļuve R-Matrix elementiem
Mēs varam piekļūt elementiem R matricās, izmantojot to pašu vienošanos, kas tiek ievērota datu rāmjos. Tātad jums būs matrica, kurai seko kvadrātiekava ar komatu starp masīviem.
Vērtība pirms komata tiek izmantota, lai piekļūtu rindām, un vērtība, kas atrodas pēc komata, tiek izmantota, lai piekļūtu kolonnām. Ilustrēsim to, izmantojot vienkāršu R kodu.
Piekļuve rindām:
R
# R program to illustrate> # access rows in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> # Accessing first and second row> cat>(>'Accessing first and second row
'>)> print>(A[1:2, ])> |
>
>Izvade
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 Accessing first and second row [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6>
Piekļuve kolonnām:
R
# R program to illustrate> # access columns in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> # Accessing first and second column> cat>(>'Accessing first and second column
'>)> print>(A[, 1:2])> |
>
>Izvade
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 Accessing first and second column [,1] [,2] [1,] 1 2 [2,] 4 5 [3,] 7 8>
Papildu piemērs, kā piekļūt R-matricas elementiem:
R
# R program to illustrate> # access an entry in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> # Accessing 2> print>(A[1, 2])> # Accessing 6> print>(A[2, 3])> |
>
>Izvade
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 [1] 2 [1] 6>
Piekļuve R apakšmatricām:
Mēs varam piekļūt apakšmatricai matricā, izmantojot kols(:) operators.
R
nat vs gulta
# R program to illustrate> # access submatrices in a matrix> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> cat>(>'Accessing the first three rows and the first two columns
'>)> print>(A[1:3, 1:2])> |
>
>Izvade
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 Accessing the first three rows and the first two columns [,1] [,2] [1,] 1 2 [2,] 4 5 [3...>
R-matricas elementu modificēšana
R var modificēt matricu elementus ar tiešu piešķiršanu.
Piemērs:
R
# R program to illustrate> # editing elements in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> # Editing the 3rd rows and 3rd column element> # from 9 to 30> # by direct assignments> A[3, 3] = 30> cat>(>'After edited the matrix
'>)> print>(A)> |
>
>Izvade
pd sapludināšana
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 After edited the matrix [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 30>
R-matricas savienošana
Matricas konkatenācija attiecas uz esošas R matricas rindu vai kolonnu sapludināšanu.
Rindas savienošana:
Rindas savienošana ar matricu tiek veikta, izmantojot rbind() .
R
# R program to illustrate> # concatenation of a row in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> # Creating another 1x3 matrix> B =>matrix>(> >c>(10, 11, 12),> >nrow = 1,> >ncol = 3> )> cat>(>'The 1x3 matrix:
'>)> print>(B)> # Add a new row using rbind()> C =>rbind>(A, B)> cat>(>'After concatenation of a row:
'>)> print>(C)> |
>
>Izvade
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 The 1x3 matrix: [,1] [,2] [,3] [1,] 10 11 12 After concatenation of a row: [,1] [,2] [,3...>
Kolonnas savienošana:
Kolonnas savienošana ar matricu tiek veikta, izmantojot cbind() .
R
# R program to illustrate> # concatenation of a column in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> # Creating another 3x1 matrix> B =>matrix>(> >c>(10, 11, 12),> >nrow = 3,> >ncol = 1,> >byrow =>TRUE> )> cat>(>'The 3x1 matrix:
'>)> print>(B)> # Add a new column using cbind()> C =>cbind>(A, B)> cat>(>'After concatenation of a column:
'>)> print>(C)> |
>
>Izvade
The 3x3 matrix: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 The 3x1 matrix: [,1] [1,] 10 [2,] 11 [3,] 12 After concatenation of a column: [,1] [,2] ...>
Izmēru neatbilstība: Ņemiet vērā, ka pirms šīs matricas savienošanas jums ir jāpārliecinās par izmēru konsekvenci starp matricu.
R
# R program to illustrate> # Dimension inconsistency in metrics concatenation> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'The 3x3 matrix:
'>)> print>(A)> # Creating another 1x3 matrix> B =>matrix>(> >c>(10, 11, 12),> >nrow = 1,> >ncol = 3,> )> cat>(>'The 1x3 matrix:
'>)> print>(B)> # This will give an error> # because of dimension inconsistency> C =>cbind>(A, B)> cat>(>'After concatenation of a column:
'>)> print>(C)> |
>
>
Izvade:
The 3x3 matrix: [, 1] [, 2] [, 3] [1, ] 1 2 3 [2, ] 4 5 6 [3, ] 7 8 9 The 1x3 matrix: [, 1] [, 2] [, 3] [1, ] 10 11 12 Error in cbind(A, B) : number of rows of matrices must match (see arg 2)>
Rindu un kolonnu pievienošana R-matricā
Lai pievienotu rindu R-matricā, varat izmantot rbind() funkciju un, lai pievienotu kolonnu R-matricai, varat izmantot cbind () funkcija.
Tiek pievienota rinda
Apskatīsim tālāk piemēru, kā pievienot rindu R-matricā?
Piemērs:
R
# Create a 3x3 matrix> number <->matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'Before inserting a new row:
'>)> print>(number)> # New row to be inserted> new_row <->c>(10, 11, 12)># Define the new row> # Inserting the new row at the second position> A <->rbind>(number[1, ], new_row, number[-1, ])> cat>(>'
After inserting a new row:
'>)> print>(number)> |
>
>Izvade
Before inserting a new row: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 After inserting a new row: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,]...>
Kolonnas pievienošana
Tālāk aplūkosim piemēru, kā pievienot kolonnu R-matricā?
R
# Create a 3x3 matrix> number <->matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'Before adding a new column:
'>)> print>(number)> # New column to be added> new_column <->c>(10, 11, 12)># Define the new column> # Adding the new column at the end> number <->cbind>(number, new_column)> cat>(>'
After adding a new column:
'>)> print>(number)> |
>
>Izvade
Before adding a new column: [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 After adding a new column: new_column [1,] 1 2 3 10 [2,] 4 5 6 1...>
R-matricas rindu un kolonnu dzēšana
Lai izdzēstu rindu vai kolonnu, vispirms ir jāpiekļūst šai rindai vai kolonnai un pēc tam pirms šīs rindas vai kolonnas jāievieto negatīva zīme. Tas norāda, ka jums bija jāizdzēš šī rinda vai kolonna.
Rindas dzēšana:
R
java nosaukumu piešķiršanas konvencija
# R program to illustrate> # row deletion in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'Before deleting the 2nd row
'>)> print>(A)> # 2nd-row deletion> A = A[-2, ]> cat>(>'After deleted the 2nd row
'>)> print>(A)> |
>
>Izvade
Before deleting the 2nd row [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 After deleted the 2nd row [,1] [,2] [,3] [1,] 1 2 3 [2,] 7 8 9>
Kolonnas dzēšana:
R
# R program to illustrate> # column deletion in metrics> # Create a 3x3 matrix> A =>matrix>(> >c>(1, 2, 3, 4, 5, 6, 7, 8, 9),> >nrow = 3,> >ncol = 3,> >byrow =>TRUE> )> cat>(>'Before deleting the 2nd column
'>)> print>(A)> # 2nd-row deletion> A = A[, -2]> cat>(>'After deleted the 2nd column
'>)> print>(A)> |
>
>Izvade
Before deleting the 2nd column [,1] [,2] [,3] [1,] 1 2 3 [2,] 4 5 6 [3,] 7 8 9 After deleted the 2nd column [,1] [,2] [1,] 1 3 [2,] 4 6 [3,] 7 9>
Mēs esam apsprieduši R-matricas un to pamatdarbības, piemēram, jaunu rindu un kolonnu pievienošanu, rindu un kolonnu dzēšanu, matricu apvienošanu utt.
Cerams, ka tas jums palīdzēja izprast R matricas, un tagad varat ērti izmantot R matricas savos projektos.
Pārbaudiet arī:
- R – masīvs
- R – saraksti
- R – Tuples
