A Rindas datu struktūra ir datorzinātņu pamatjēdziens, ko izmanto datu glabāšanai un pārvaldībai noteiktā secībā. Tas izriet no principa Pirmais iekšā, pirmais ārā (FIFO) , kur pirmais rindai pievienotais elements ir pirmais, kas tiek noņemts. Rindas parasti izmanto dažādos algoritmos un lietojumprogrammās to vienkāršības un efektivitātes dēļ datu plūsmas pārvaldībā.

Rindas datu struktūra

Satura rādītājs

• Rindas lietojumprogrammas
• Queue implementācijas dažādās programmēšanas valodās
• Kas ir rinda datu struktūrās?

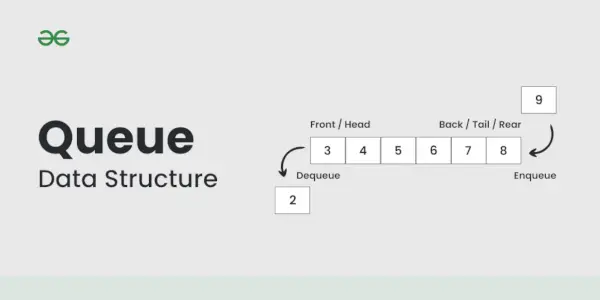
  Rinda ir lineāra datu struktūra, kas seko Pirmais iekšā-pirmais ārā (FIFO) principu. Tas darbojas kā līnija, kuras vienā galā tiek pievienoti elementi ( aizmugure ) un izņemta no otra gala ( priekšā ).

  Atsaukt no rindas (dzēst) : noņem un atgriež elementu no rindas priekšpuses.

• Palūrēt : atgriež rindas sākumā esošo elementu, to nenoņemot.
• Tukšs : pārbauda, ​​vai rinda ir tukša.
• Pilns : pārbauda, ​​vai rinda ir pilna.

• Rinda C++ standarta veidņu bibliotēkā (STL)
• Rindas interfeiss Java
• Rinda programmā Python
• Rinda C#
• Rinda Javascript

Ieviesiet steku, izmantojot vienu rindu

Īstenojiet rindu, izmantojot skursteņus

Kā efektīvi ieviest k rindas vienā masīvā?

LRU kešatmiņas ieviešana

Noteikt ciklu nevirzītā grafikā, izmantojot BFS

Platuma pirmā meklēšana vai BFS diagrammai

Java direktorija šķērsošana, izmantojot BFS

Binārā koka vertikālā secība, izmantojot karti

Drukāt binārā koka labo skatu

Atrodiet binārā koka minimālo dziļumu

Pārbaudiet, vai dotais grafiks ir divpusējs vai nē

Līmenis ar maksimālo mezglu skaitu

Atrodiet, vai virzītā grafā ir ceļš starp divām virsotnēm

Drukājiet visus mezglus starp diviem norādītajiem līmeņiem Binārajā kokā

Atrodiet dotās atslēgas nākamo labo mezglu

Minimālie soļi, lai bruņinieks sasniegtu mērķi

Salas grafikā, izmantojot BFS

Līmeņa secības šķērsošana rindu pa rindiņai | 3. kopa (izmantojot vienu rindu)

Atrodiet pirmo rakstzīmi, kas neatkārtojas no rakstzīmju straumes

Plūdu piepildīšanas algoritms

Minimālais laiks, kas nepieciešams visu apelsīnu sapuvšanai

Īsākais ceļš binārajā labirintā

Interesanta metode bināro skaitļu ģenerēšanai no 1 līdz n

Maksimālo izmaksu ceļš no avota mezgla līdz galamērķim

Īsākais attālums starp divām šūnām matricā vai režģī

Čūskas un kāpņu problēma

Atrodiet īsāko drošo ceļu ceļā ar kājnieku mīnām

Saskaitiet visus iespējamos gājienus no avota līdz galamērķim ar precīzi K malām

Vienkāršā ceļa minimālās izmaksas starp diviem mezgliem virzītā un svērtā diagrammā

Minimālo izmaksu ceļš virzītā diagrammā, izmantojot noteiktu starpmezglu kopu

Atrodiet pirmo apļveida ceļvedi, kas apmeklē visus benzīna sūkņus

Ātrās saites:

• 'Video' rindā
• Ieteicams:
  • Uzziniet datu struktūru un algoritmus | DSA apmācība
  • Rinda Go valodā
  • Rinda Scalā