Datorzinātnēs pastāv dažas problēmas, kuru risinājumi vēl nav atrasti, problēmas ir sadalītas klasēs, kas pazīstamas kā Sarežģītības klases . Sarežģītības teorijā sarežģītības klase ir problēmu kopums ar saistītu sarežģītību. Šīs nodarbības palīdz zinātniekiem grupēt problēmas, pamatojoties uz to, cik daudz laika un vietas tām nepieciešams, lai atrisinātu problēmas un pārbaudītu risinājumus. Tā ir skaitļošanas teorijas nozare, kas nodarbojas ar resursiem, kas nepieciešami problēmas risināšanai.
ms Word ātrās piekļuves rīkjosla
Kopējie resursi ir laiks un telpa, kas nozīmē, cik daudz laika algoritmam nepieciešams, lai atrisinātu problēmu, un atbilstošo atmiņas lietojumu.
- Algoritma laika sarežģītību izmanto, lai aprakstītu problēmas atrisināšanai nepieciešamo darbību skaitu, taču to var izmantot arī, lai aprakstītu, cik ilgs laiks nepieciešams atbildes pārbaudei.
- Algoritma telpas sarežģītība apraksta, cik daudz atmiņas ir nepieciešams algoritma darbībai.
Sarežģītības nodarbības ir noderīgas līdzīga veida problēmu organizēšanā.
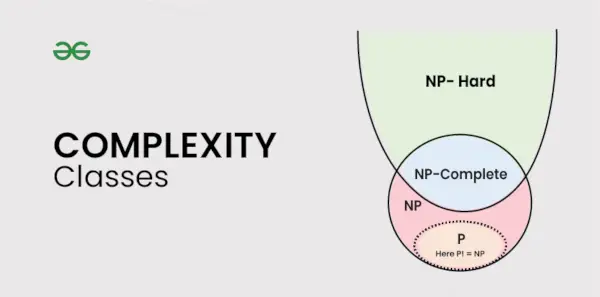
Sarežģītības klašu veidi
Šajā rakstā ir apskatītas šādas sarežģītības klases:
- P klase
- NP klase
- CoNP klase
- NP-grūti
- NP-pilnīgs
P klase
P klasē P apzīmē Polinoma laiks. Tā ir lēmumu problēmu kolekcija (problēmas ar atbildi jā vai nē), ko var atrisināt ar deterministisku mašīnu polinoma laikā.
Iespējas:
- Risinājums, lai P problēma s ir viegli atrast.
- P bieži vien ir skaitļošanas problēmu klase, kuras ir atrisināmas un izsekojamas. Izsekojamais nozīmē, ka problēmas var atrisināt gan teorētiski, gan praktiski. Bet problēmas, kuras var atrisināt teorētiski, bet ne praksē, sauc par neatrisināmām.
Šajā klasē ir daudz problēmu:
- Lielākā kopīgā dalītāja aprēķināšana.
- Maksimālās atbilstības atrašana.
- Sapludināt Kārtot
NP klase
NP NP klasē apzīmē Nedeterministiskais polinoma laiks . Tas ir lēmumu problēmu kopums, ko var atrisināt ar nedeterministisku mašīnu polinoma laikā.
Iespējas:
- NP klases risinājumus ir grūti atrast, jo tos risina nedeterministiska mašīna, taču risinājumus ir viegli pārbaudīt.
- NP problēmas var pārbaudīt ar Tjūringa mašīnu polinoma laikā.
Piemērs:
pārdēvējiet Linux mapi
Apskatīsim piemēru, lai labāk izprastu NP klase . Pieņemsim, ka pastāv uzņēmums, kura kopējais skaits ir 1000 darbinieki ar unikālu darbinieku ID . Pieņemsim, ka tādi ir 200 viņiem pieejamas telpas. Izlase no 200 darbinieki ir jāsavieno pārī, bet uzņēmuma vadītāja rīcībā ir dati par dažiem darbiniekiem, kuri personisku iemeslu dēļ nevar strādāt vienā telpā.
Šis ir piemērs an E.G problēma. Tā kā ir viegli pārbaudīt, vai dotā izvēle 200 kolēģa ieteiktie darbinieki ir apmierinoši vai nē, t.i., neviens pāris, kas ņemts no kolēģu saraksta, neparādās izpilddirektora norādītajā sarakstā. Taču šāda saraksta izveide no nulles šķiet tik grūta, ka tas ir pilnīgi nepraktiski.
Tas norāda, ka, ja kāds var sniegt mums problēmas risinājumu, mēs varam atrast pareizo un nepareizo pāri polinoma laikā. Tādējādi priekš E.G klases uzdevums, ir iespējama atbilde, kuru var aprēķināt polinoma laikā.
Šajā klasē ir daudzas problēmas, kuras vēlaties efektīvi atrisināt:
- Būla apmierinātības problēma (SAT).
- Hamiltona ceļa problēma.
- Grafiku krāsošana.
Co-NP klase
Co-NP apzīmē NP klases papildinājumu. Tas nozīmē, ja atbilde uz problēmu Co-NP ir nē, tad ir pierādījums, ko var pārbaudīt polinoma laikā.
Iespējas:
java objektu vienlīdzība
- Ja problēma X atrodas NP, tad tās papildinājums X’ ir arī CoNP.
- NP un CoNP problēmai nav nepieciešams pārbaudīt visas atbildes uzreiz polinoma laikā, ir nepieciešams pārbaudīt tikai vienu konkrētu atbildi jā vai nē polinoma laikā, lai problēma būtu NP vai CoNP.
Daži CoNP problēmu piemēri ir:
- Lai pārbaudītu pirmskaitli.
- Veselu skaitļu faktorizācija.
NP-hard klase
NP sarežģīta problēma ir vismaz tikpat smaga kā NP smagākā problēma, un tā ir tādu problēmu klase, ka katra NP problēma tiek samazināta līdz NP smagai.
Iespējas:
- Visas NP sarežģītās problēmas nav NP.
- Lai tos pārbaudītu, ir nepieciešams ilgs laiks. Tas nozīmē, ka, ja tiek sniegts NP smagas problēmas risinājums, ir nepieciešams ilgs laiks, lai pārbaudītu, vai tas ir pareizs vai nē.
- Problēma A ir NP grūti, ja katrai NP problēmai L pastāv polinoma laika samazinājums no L uz A.
Daži no Np-hard problēmu piemēriem ir:
- Apturēšanas problēma.
- Kvalificētas Būla formulas.
- Nav Hamiltona cikla.
NP-pilna klase
Problēma ir NP-pilnīga, ja tā ir gan NP, gan NP-grūta. Pilnīgas NP problēmas ir NP smagās problēmas.
Iespējas:
- NP-pilnīgas problēmas ir īpašas, jo jebkura NP klases problēma var tikt pārveidota vai reducēta par NP-pilnīgām problēmām polinoma laikā.
- Ja varētu atrisināt NP pilnu uzdevumu polinoma laikā, tad var atrisināt arī jebkuru NP uzdevumu polinoma laikā.
Daži problēmu piemēri:
- Hamiltona cikls.
- Apmierināmība.
- Virsotnes vāks .
| Sarežģītības klase | Raksturīga iezīme |
| P | Viegli atrisināms polinoma laikā. |
| E.G | Jā, atbildes var pārbaudīt polinoma laikā. |
| Co-NP | Nē, atbildes var pārbaudīt polinoma laikā. |
| NP-grūti | Visas NP-hard problēmas nav NP, un ir nepieciešams ilgs laiks, lai tās pārbaudītu. |
| NP-pilnīgs | Problēma, kas ir NP un NP grūti, ir NP-pilnīga. |
