• Naive Bayes algoritms ir uzraudzīts mācīšanās algoritms, kura pamatā ir Bayes teorēma un izmanto klasifikācijas problēmu risināšanai.
• To galvenokārt izmanto teksta klasifikācija kas ietver augstas dimensijas apmācības datu kopu.
• Naive Bayes klasifikators ir viens no vienkāršākajiem un efektīvākajiem klasifikācijas algoritmiem, kas palīdz izveidot ātrus mašīnmācīšanās modeļus, kas var ātri prognozēt.
Tas ir varbūtības klasifikators, kas nozīmē, ka tas prognozē, pamatojoties uz objekta varbūtību.
• Daži populāri Naiv Bayes algoritma piemēri ir surogātpasta filtrēšana, sentimentālā analīze un rakstu klasificēšana .

Kāpēc to sauc par Naive Bayes?

Naive Bayes algoritms sastāv no diviem vārdiem Naive un Bayes, kurus var raksturot kā:

Naivi: To sauc par naivu, jo tiek pieņemts, ka noteiktas pazīmes rašanās nav atkarīga no citu pazīmju rašanās. Piemēram, ja augļus identificē pēc krāsas, formas un garšas, tad sarkans, sfērisks un salds auglis tiek atpazīts par ābolu. Tādējādi katra iezīme atsevišķi palīdz noteikt, ka tas ir ābols, neatkarīgi viens no otra.Bayes: To sauc par Bayes, jo tas ir atkarīgs no Beijes teorēmas principa.

Beijesa teorēma:

• Bayes teorēma ir pazīstama arī kā Beijesa noteikums vai Beijesa likums , ko izmanto, lai noteiktu hipotēzes varbūtību ar priekšzināšanām. Tas ir atkarīgs no nosacītās varbūtības.
• Beijesa teorēmas formula ir dota šādi:

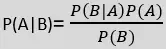
kur,

rinda un kolonna

P(A|B) ir aizmugures varbūtība : Hipotēzes A varbūtība par novēroto notikumu B.

P(B|A) ir varbūtības varbūtība : pierādījumu varbūtība, ņemot vērā, ka hipotēzes varbūtība ir patiesa.

P(A) ir iepriekšējā varbūtība : hipotēzes varbūtība pirms pierādījumu novērošanas.

P(B) ir robežvarbūtība : Pierādījumu iespējamība.

Naivā Beijesa klasifikatora darbība:

Naive Bayes klasifikatora darbību var saprast, izmantojot tālāk norādīto piemēru:

Pieņemsim, ka mums ir datu kopa laika apstākļi un atbilstošais mērķa mainīgais ' Spēlēt '. Tāpēc, izmantojot šo datu kopu, mums ir jāizlemj, vai mums vajadzētu spēlēt vai nē konkrētā dienā atbilstoši laika apstākļiem. Tātad, lai atrisinātu šo problēmu, mums ir jāveic šādas darbības:

1. Konvertējiet doto datu kopu biežuma tabulās.
2. Izveidojiet varbūtības tabulu, atrodot doto pazīmju varbūtības.
3. Tagad izmantojiet Bayes teorēmu, lai aprēķinātu aizmugurējo varbūtību.

Problēma : Ja laiks ir saulains, tad Spēlētājam jāspēlē vai nē?

Risinājums : Lai to atrisinātu, vispirms apsveriet tālāk norādīto datu kopu.

Laikapstākļu biežuma tabula:

Laika apstākļi varbūtības tabulā:

Lietojot Beijesa teorēmu:

P(Jā|saulains)= P(saulains|Jā)*P(Jā)/P(saulains)

P(saulains|jā)= 3/10= 0,3

P(saulains)= 0,35

P(Jā)=0,71

java savienojamība

Tātad P(jā|saulains) = 0,3*0,71/0,35= 0,60

P(nē|saulains)= P(saulains|nē)*P(nē)/P(saulains)

P(saulains|NO)= 2/4=0,5

P(Nē)= 0,29

P(saulains)= 0,35

Tātad P(nē|saulains)= 0,5*0,29/0,35 = 0.41

Tātad, kā mēs redzam no iepriekš minētā aprēķina, ka P(jā|saulains)>P(nē|saulains)

Tādējādi saulainā dienā spēlētājs var spēlēt spēli.

Naive Bayes klasifikatora priekšrocības:

• Naive Bayes ir viens no ātrajiem un vienkāršajiem ML algoritmiem datu kopu klases prognozēšanai.
• To var izmantot gan binārajai, gan vairāku klašu klasifikācijai.
• Salīdzinājumā ar citiem algoritmiem tas labi darbojas vairāku klašu prognozēs.
• Tā ir vispopulārākā izvēle teksta klasifikācijas problēmas .

Naive Bayes klasifikatora trūkumi:

• Naive Bayes pieņem, ka visas pazīmes ir neatkarīgas vai nesaistītas, tāpēc tas nevar uzzināt saistību starp pazīmēm.

Naive Bayes klasifikatora pielietojumi:

• To lieto, lai Kredīta vērtēšana .
• Tas tiek izmantots medicīnisko datu klasifikācija .
• To var izmantot reāllaika prognozes jo Naive Bayes klasifikators ir dedzīgs mācīšanās.
• To izmanto teksta klasifikācijā, piemēram, Surogātpasta filtrēšana un Sentimenta analīze .

Naivā Bayes modeļa veidi:

Ir trīs Naive Bayes modeļa veidi, kas ir norādīti zemāk:

apakšvirkne bash

Gausa: Gausa modelis pieņem, ka pazīmes seko normālam sadalījumam. Tas nozīmē, ja prognozētāji ņem nepārtrauktas vērtības, nevis diskrētas, tad modelī tiek pieņemts, ka šīs vērtības tiek ņemtas no Gausa sadalījuma.Multinomiāls: Multinomial Naive Bayes klasifikators tiek izmantots, ja dati ir sadalīti vairākos nominālos. To galvenokārt izmanto dokumentu klasifikācijas problēmām, tas nozīmē, ka konkrēts dokuments pieder kādai kategorijai, piemēram, sports, politika, izglītība utt.
Klasifikators prognozētājiem izmanto vārdu biežumu.Bernulli: Bernulli klasifikators darbojas līdzīgi Multinomial klasifikatoram, bet prognozēšanas mainīgie ir neatkarīgi Būla mainīgie. Piemēram, vai konkrēts vārds dokumentā ir vai nav. Šis modelis ir slavens arī ar dokumentu klasifikācijas uzdevumiem.

Naivā Beijesa algoritma Python ieviešana:

Tagad mēs ieviesīsim naivu Bayes algoritmu, izmantojot Python. Tāpēc šim nolūkam mēs izmantosim lietotāja_dati ' datu kopa , ko esam izmantojuši savā citā klasifikācijas modelī. Tāpēc mēs varam viegli salīdzināt Naive Bayes modeli ar citiem modeļiem.

Īstenošanas soļi:

• Datu priekšapstrādes solis
• Naive Bayes pielāgošana treniņu komplektam
• Pārbaudes rezultāta prognozēšana
• Rezultāta precizitātes pārbaude (apjukuma matricas izveide)
• Testa kopas rezultāta vizualizācija.

1) Datu priekšapstrādes solis:

Šajā darbībā mēs iepriekš apstrādāsim/sagatavosim datus, lai varētu tos efektīvi izmantot savā kodā. Tas ir līdzīgi kā mēs to darījām datu priekšapstrādē. Kods tam ir norādīts zemāk:

 Importing the libraries import numpy as nm import matplotlib.pyplot as mtp import pandas as pd # Importing the dataset dataset = pd.read_csv('user_data.csv') x = dataset.iloc[:, [2, 3]].values y = dataset.iloc[:, 4].values # Splitting the dataset into the Training set and Test set from sklearn.model_selection import train_test_split x_train, x_test, y_train, y_test = train_test_split(x, y, test_size = 0.25, random_state = 0) # Feature Scaling from sklearn.preprocessing import StandardScaler sc = StandardScaler() x_train = sc.fit_transform(x_train) x_test = sc.transform(x_test) 

Iepriekš minētajā kodā mēs esam ielādējuši datu kopu mūsu programmā, izmantojot datu kopa = pd.read_csv('user_data.csv') . Ielādētā datu kopa ir sadalīta apmācības un pārbaudes kopā, un pēc tam esam mērogojuši līdzekļa mainīgo.

Datu kopas izvade tiek dota šādi:

2) Naive Bayes pievienošana treniņu komplektam:

Pēc priekšapstrādes soļa mēs Naive Bayes modeli pievienosim apmācības komplektam. Zemāk ir tā kods:

 # Fitting Naive Bayes to the Training set from sklearn.naive_bayes import GaussianNB classifier = GaussianNB() classifier.fit(x_train, y_train) 

Iepriekš minētajā kodā mēs esam izmantojuši GaussianNB klasifikators lai to pielāgotu apmācības datu kopai. Mēs varam izmantot arī citus klasifikatorus atbilstoši mūsu prasībām.

Izvade:

 Out[6]: GaussianNB(priors=None, var_smoothing=1e-09) 

3) Testa komplekta rezultāta prognozēšana:

Tagad mēs prognozēsim testa komplekta rezultātu. Šim nolūkam mēs izveidosim jaunu prognozēšanas mainīgo y_pred , un izmantos prognozēšanas funkciju, lai veiktu prognozes.

 # Predicting the Test set results y_pred = classifier.predict(x_test) 

Izvade:

Iepriekšējā izvade parāda prognozēšanas vektora rezultātu y_pred un reālā vektora y_tests. Mēs redzam, ka dažas prognozes atšķiras no reālajām vērtībām, kas ir nepareizas prognozes.

4) Apjukuma matricas izveide:

Tagad mēs pārbaudīsim Naive Bayes klasifikatora precizitāti, izmantojot Confusion matricu. Zemāk ir tā kods:

 # Making the Confusion Matrix from sklearn.metrics import confusion_matrix cm = confusion_matrix(y_test, y_pred) 

Izvade:

Kā redzams iepriekš sniegtajā neskaidrības matricas izvadē, ir 7+3=10 nepareizas prognozes un 65+25=90 pareizas prognozes.

5) Treniņkomplekta rezultāta vizualizēšana:

Tālāk mēs vizualizēsim treniņu komplekta rezultātu, izmantojot Na�ve Bayes klasifikatoru. Zemāk ir tā kods:

 # Visualising the Training set results from matplotlib.colors import ListedColormap x_set, y_set = x_train, y_train X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (Training set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Izvade:

Iepriekš minētajā izvadā mēs redzam, ka Na�ve Bayes klasifikators ir atdalījis datu punktus ar precīzu robežu. Tā ir Gausa līkne, kā mēs esam izmantojuši Gauss NB klasifikators mūsu kodā.

6) Testa kopas rezultāta vizualizācija:

 # Visualising the Test set results from matplotlib.colors import ListedColormap x_set, y_set = x_test, y_test X1, X2 = nm.meshgrid(nm.arange(start = x_set[:, 0].min() - 1, stop = x_set[:, 0].max() + 1, step = 0.01), nm.arange(start = x_set[:, 1].min() - 1, stop = x_set[:, 1].max() + 1, step = 0.01)) mtp.contourf(X1, X2, classifier.predict(nm.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha = 0.75, cmap = ListedColormap(('purple', 'green'))) mtp.xlim(X1.min(), X1.max()) mtp.ylim(X2.min(), X2.max()) for i, j in enumerate(nm.unique(y_set)): mtp.scatter(x_set[y_set == j, 0], x_set[y_set == j, 1], c = ListedColormap(('purple', 'green'))(i), label = j) mtp.title('Naive Bayes (test set)') mtp.xlabel('Age') mtp.ylabel('Estimated Salary') mtp.legend() mtp.show() 

Izvade:

Iepriekš minētā izvade ir testa kopas datu galīgā izvade. Kā redzams, klasifikators ir izveidojis Gausa līkni, lai sadalītu mainīgos “pirktos” un “nepirktos”. Ir dažas nepareizas prognozes, kuras esam aprēķinājuši Confusion matricā. Bet tomēr tas ir diezgan labs klasifikators.

apakšvirknes metode Java