Reālajā pasaulē mašīnmācība lietojumprogrammām, parasti ir daudzas atbilstošas funkcijas, taču var būt novērojama tikai daļa no tām. Strādājot ar mainīgajiem, kas dažreiz ir novērojami un dažreiz nē, patiešām ir iespējams izmantot gadījumus, kad šis mainīgais ir redzams vai novērots, lai uzzinātu un veiktu prognozes gadījumiem, kad tas nav novērojams. Šo pieeju bieži dēvē par trūkstošo datu apstrādi. Izmantojot pieejamos gadījumus, kad mainīgais ir novērojams, mašīnmācīšanās algoritmi var apgūt modeļus un attiecības no novērotajiem datiem. Pēc tam šos apgūtos modeļus var izmantot, lai prognozētu mainīgā lieluma vērtības gadījumos, kad tā trūkst vai nav novērojama.
Gaidījumu maksimizēšanas algoritmu var izmantot, lai risinātu situācijas, kurās mainīgie ir daļēji novērojami. Ja daži mainīgie ir novērojami, mēs varam izmantot šos gadījumus, lai uzzinātu un novērtētu to vērtības. Tad mēs varam paredzēt šo mainīgo vērtības gadījumos, kad tas nav novērojams.
EM algoritms tika ierosināts un nosaukts pamatrakstā, ko 1977. gadā publicēja Arturs Dempsters, Nans Lairds un Donalds Rubins. Viņu darbs formalizēja algoritmu un parādīja tā lietderību statistiskajā modelēšanā un novērtēšanā.
EM algoritms ir piemērojams latentiem mainīgajiem, kas ir mainīgie, kas nav tieši novērojami, bet ir izsecināti no citu novēroto mainīgo vērtībām. Izmantojot zināmo vispārējo varbūtības sadalījuma formu, kas regulē šos latentos mainīgos, EM algoritms var paredzēt to vērtības.
EM algoritms kalpo par pamatu daudziem nepārraudzītiem klasterizācijas algoritmiem mašīnmācības jomā. Tas nodrošina sistēmu, lai atrastu statistiskā modeļa lokālos maksimālās iespējamības parametrus un izsecinātu latentos mainīgos gadījumos, kad trūkst datu vai tie ir nepilnīgi.
Expectation-Maximization (EM) algoritms
Expectation-Maximization (EM) algoritms ir iteratīva optimizācijas metode, kas apvieno dažādas bez uzraudzības mašīnmācība algoritmus, lai atrastu parametru maksimālo iespējamību vai maksimālos aizmugures aplēses statistikas modeļos, kas ietver nenovērotus latentus mainīgos. EM algoritmu parasti izmanto latentiem mainīgo modeļiem, un tas var apstrādāt trūkstošos datus. Tas sastāv no aplēses soļa (E-solis) un maksimizācijas posma (M-solis), veidojot iteratīvu procesu, lai uzlabotu modeļa piemērotību.
- E solī algoritms aprēķina latentos mainīgos, t.i., loga varbūtības prognozi, izmantojot pašreizējos parametru aprēķinus.
- M solī algoritms nosaka parametrus, kas maksimāli palielina sagaidāmo E solī iegūto log-iespējamību, un atbilstošie modeļa parametri tiek atjaunināti, pamatojoties uz aplēstiem latentiem mainīgajiem.

Cerības-maksimizācija EM algoritmā
Iteratīvi atkārtojot šīs darbības, EM algoritms cenšas maksimāli palielināt novēroto datu iespējamību. To parasti izmanto neuzraugotiem mācību uzdevumiem, piemēram, klasteru veidošanai, kur tiek secināti latenti mainīgie, un to var izmantot dažādās jomās, tostarp mašīnmācībā, datorredzēšanā un dabiskās valodas apstrādē.
Galvenie termini gaidu maksimizēšanas (EM) algoritmā
Daži no visbiežāk izmantotajiem galvenajiem terminiem gaidu maksimizēšanas (EM) algoritmā ir šādi:
- Latentie mainīgie: latentie mainīgie ir nenovēroti mainīgie statistikas modeļos, kurus var secināt tikai netieši, izmantojot to ietekmi uz novērojamajiem mainīgajiem. Tos nevar tieši izmērīt, bet tos var noteikt pēc to ietekmes uz novērojamajiem mainīgajiem. Varbūtība: tā ir doto datu novērošanas varbūtība, ņemot vērā modeļa parametrus. EM algoritmā mērķis ir atrast parametrus, kas palielina iespējamību. Log-Likelihood: tas ir iespējamības funkcijas logaritms, kas mēra atbilstību starp novērotajiem datiem un modeli. EM algoritms cenšas maksimāli palielināt log-iespējamību. Maksimālās varbūtības novērtējums (MLE) : MLE ir metode, lai novērtētu statistiskā modeļa parametrus, atrodot parametru vērtības, kas maksimāli palielina iespējamības funkciju, kas mēra, cik labi modelis izskaidro novērotos datus. Aizmugurējā varbūtība: Bajesa secinājuma kontekstā EM algoritmu var paplašināt, lai novērtētu maksimālos a posteriori (MAP) aprēķinus, kur parametru posterior varbūtība tiek aprēķināta, pamatojoties uz iepriekšējo sadalījumu un iespējamības funkciju. Gaidīšanas (E) solis: EM algoritma E-solis aprēķina latento mainīgo paredzamo vērtību vai posterioro varbūtību, ņemot vērā novērotos datus un pašreizējos parametru aplēses. Tas ietver katra latentā mainīgā varbūtības aprēķināšanu katram datu punktam. Maksimizācijas (M) solis: EM algoritma M-solis atjaunina parametru aplēses, maksimāli palielinot paredzamo log-iespējamību, kas iegūta no E-soļa. Tas ietver parametru vērtību atrašanu, kas optimizē varbūtības funkciju, parasti izmantojot skaitliskās optimizācijas metodes. Konverģence: Konverģence attiecas uz stāvokli, kad EM algoritms ir sasniedzis stabilu risinājumu. Parasti to nosaka, pārbaudot, vai izmaiņas loga varbūtībā vai parametru aplēsēs ir zemākas par iepriekš noteiktu slieksni.
Kā darbojas cerību maksimizēšanas (EM) algoritms:
Expectation-Maximization algoritma būtība ir izmantot pieejamos novērotos datu kopas datus, lai novērtētu trūkstošos datus, un pēc tam izmantot šos datus, lai atjauninātu parametru vērtības. Ļaujiet mums sīkāk izprast EM algoritmu.

EM algoritma blokshēma
- Inicializācija:
- Sākotnēji tiek ņemta vērā parametru sākotnējo vērtību kopa. Nepilnīgu novēroto datu kopa tiek dota sistēmai ar pieņēmumu, ka novērotie dati nāk no konkrēta modeļa.
- Aprēķiniet katra latentā mainīgā posterioro varbūtību vai atbildību, ņemot vērā novērotos datus un pašreizējos parametru aplēses.
- Novērtējiet trūkstošās vai nepilnīgās datu vērtības, izmantojot pašreizējos parametru aprēķinus.
- Aprēķiniet novēroto datu logaritmisko varbūtību, pamatojoties uz pašreizējiem parametru aprēķiniem un aplēstajiem trūkstošajiem datiem.
- Atjauniniet modeļa parametrus, maksimāli palielinot paredzamo pilnīgo datu žurnāla iespējamību, kas iegūta no E-soļa.
- Tas parasti ietver optimizācijas problēmu risināšanu, lai atrastu parametru vērtības, kas palielina žurnāla varbūtību.
- Konkrētā izmantotā optimizācijas metode ir atkarīga no problēmas veida un izmantotā modeļa.
- Pārbaudiet konverģenci, salīdzinot loga varbūtības izmaiņas vai parametru vērtības starp iterācijām.
- Ja izmaiņas ir zemākas par iepriekš noteiktu slieksni, apstājieties un uzskatiet, ka algoritms ir konverģēts.
- Pretējā gadījumā atgriezieties pie E-soļa un atkārtojiet procesu, līdz tiek sasniegta konverģence.
Cerību maksimizēšanas algoritms Soli pa solim ieviešana
Importējiet nepieciešamās bibliotēkas
Python3
kurš ir urfi javed
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
>
Ģenerējiet datu kopu ar diviem Gausa komponentiem
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
Izvade :

Blīvuma grafiks
f-string python
Inicializējiet parametrus
Python3
java kolekcijas ietvars
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Izpildiet EM algoritmu
- Atkārtojas noteiktajam laikmetu skaitam (šajā gadījumā 20).
- Katrā laikmetā E-solis aprēķina pienākumus (gamma vērtības), novērtējot katra komponenta Gausa varbūtības blīvumus un sverot tos ar atbilstošajām proporcijām.
- M-solis atjaunina parametrus, aprēķinot katra komponenta svērto vidējo un standarta novirzi
Python3
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Izvade :

Laikmets pret žurnāla varbūtību
ascii no a in Java
Uzzīmējiet galīgo aprēķināto blīvumu
Python3
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
>
>
Izvade :
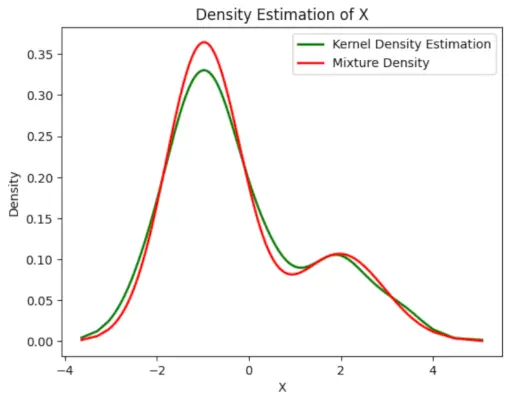
Paredzamais blīvums
Lietojumprogrammas EM algoritms
- To var izmantot, lai aizpildītu trūkstošos datus paraugā.
- To var izmantot kā pamatu klasteru nepārraudzītai apguvei.
- To var izmantot, lai novērtētu slēptā Markova modeļa (HMM) parametrus.
- To var izmantot latento mainīgo vērtību atklāšanai.
EM algoritma priekšrocības
- Vienmēr tiek garantēts, ka iespējamība palielināsies ar katru iterāciju.
- E-solis un M-solis bieži vien ir diezgan vienkāršs daudzu problēmu risināšanai ieviešanas ziņā.
- M-pakāpju risinājumi bieži pastāv slēgtā formā.
EM algoritma trūkumi
- Tam ir lēna konverģence.
- Tas veic konverģenci tikai uz vietējo optimālo.
- Tam nepieciešamas gan varbūtības, gan uz priekšu, gan atpakaļ (skaitliskajai optimizācijai nepieciešama tikai uz priekšu vērsta varbūtība).
