Kas ir datu struktūra:
Datu struktūra ir krātuve, ko izmanto datu glabāšanai un kārtošanai. Tas ir veids, kā sakārtot datus datorā, lai tiem varētu efektīvi piekļūt un tos atjaunināt.
Datu struktūra tiek izmantota ne tikai datu organizēšanai. To izmanto arī datu apstrādei, izguvei un glabāšanai. Gandrīz katrā izstrādātajā programmā vai programmatūras sistēmā tiek izmantoti dažādi pamata un uzlaboti datu struktūru veidi. Tāpēc mums ir jābūt labām zināšanām par datu struktūrām.
Datu struktūras ir neatņemama datoru sastāvdaļa, ko izmanto datu kārtošanai atmiņā. Viņi ir būtiski un atbildīgi par datu efektīvu organizēšanu, apstrādi, piekļuvi tiem un uzglabāšanu. Bet tas vēl nav viss. Dažādu veidu datu struktūrām ir savas īpašības, funkcijas, lietojumprogrammas, priekšrocības un trūkumi. Tātad, kā noteikt datu struktūru, kas ir piemērota konkrētam uzdevumam? Ko nozīmē termins “datu struktūra”? Cik datu struktūru veidu pastāv un kam tās tiek izmantotas?

Kas ir datu struktūra: veidi, klasifikācijas un lietojumprogrammas
Mēs esam jūs nodrošinājuši. Mēs esam izveidojuši pilnu sarakstu ar visu par to, kas ir datu struktūra, kādi ir datu struktūru veidi, datu struktūru klasifikācija, katras datu struktūras lietojumi utt. Šajā rakstā mēs apspriedīsim katru katras datu struktūras aspektu, lai palīdzētu jums dažu minūšu laikā izvēlēties labāko.
Satura rādītājs
- Kas ir datu struktūra?
- Kā datu struktūra atšķiras no datu veida?
- Datu struktūras klasifikācija
- Masīvi
- Saistītais saraksts
- Kaudze
- Rinda
- Koks
- Grafiks
- Secinājums
Kā datu struktūra atšķiras no datu veida:
Mēs jau esam iemācījušies par datu struktūru. Daudzas reizes cilvēki sajaucas starp datu tipu un datu struktūru. Tāpēc apskatīsim dažas atšķirības starp datu tipu un datu struktūru, lai tas būtu skaidrs.
| Datu tips | Datu struktūra |
|---|---|
| Datu tips ir mainīgā forma, kurai var piešķirt vērtību. Tas nosaka, ka konkrētais mainīgais piešķirs tikai noteiktā datu tipa vērtības. | Datu struktūra ir dažāda veida datu kopums. Visus datus var attēlot, izmantojot objektu, un tos var izmantot visā programmā. |
| Tajā var būt vērtība, bet ne dati. Tāpēc tas ir bez datiem. | Tajā vienā objektā var būt vairāku veidu dati. |
| Datu tipa ieviešana ir pazīstama kā abstrakta ieviešana. atsaukt pēdējo apņemšanos | Datu struktūras ieviešana ir pazīstama kā konkrēta ieviešana. |
| Datu tipu gadījumā nav laika sarežģītības. | Datu struktūras objektos svarīga loma ir laika sarežģītībai. |
| Datu tipu gadījumā datu vērtība netiek saglabāta, jo tā atspoguļo tikai to datu veidu, ko var uzglabāt. | Savukārt datu struktūru gadījumā dati un to vērtība ieņem vietu datora galvenajā atmiņā. Turklāt datu struktūra vienā objektā var saturēt dažāda veida un veidu datus. |
| Datu tipu piemēri ir int, float, double utt. | Datu struktūras piemēri ir kaudze, rinda, koks utt. |
Datu struktūras klasifikācija:
Datu struktūrai mūsu ikdienas dzīvē ir daudz dažādu lietojumu. Ir daudz dažādu datu struktūru, kas tiek izmantotas dažādu matemātisku un loģisku problēmu risināšanai. Izmantojot datu struktūru, salīdzinoši īsā laika periodā var sakārtot un apstrādāt ļoti lielu datu apjomu. Apskatīsim dažādas datu struktūras, kas tiek izmantotas dažādās situācijās.
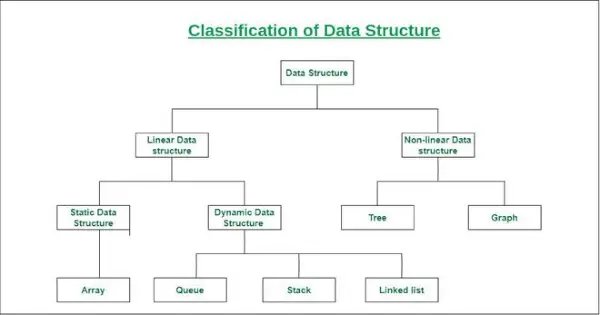
Datu struktūras klasifikācija
- Lineārā datu struktūra: Datu struktūru, kurā datu elementi ir sakārtoti secīgi vai lineāri, kur katrs elements ir pievienots tā iepriekšējam un nākamajam blakus esošajam elementam, sauc par lineāro datu struktūru.
Lineāro datu struktūru piemēri ir masīvs, steks, rinda, saistītais saraksts utt.- Statiskā datu struktūra: Statiskajai datu struktūrai ir fiksēts atmiņas lielums. Statiskās datu struktūras elementiem ir vieglāk piekļūt.
Šīs datu struktūras piemērs ir masīvs. - Dinamiskā datu struktūra: Dinamiskajā datu struktūrā lielums nav fiksēts. To var nejauši atjaunināt izpildlaikā, ko var uzskatīt par efektīvu attiecībā uz koda atmiņas (vietas) sarežģītību.
Šīs datu struktūras piemēri ir rinda, steks utt.
- Statiskā datu struktūra: Statiskajai datu struktūrai ir fiksēts atmiņas lielums. Statiskās datu struktūras elementiem ir vieglāk piekļūt.
- Nelineāra datu struktūra: Datu struktūras, kurās datu elementi nav izvietoti secīgi vai lineāri, sauc par nelineārām datu struktūrām. Nelineārā datu struktūrā mēs nevaram šķērsot visus elementus tikai vienā izpildē.
Nelineāru datu struktūru piemēri ir koki un grafiki.
Nepieciešamā datu struktūra:
Datu struktūra un algoritma sintēze ir savstarpēji saistītas. Datu noformējumam jābūt viegli saprotamam, lai izstrādātājs un lietotājs varētu efektīvi īstenot darbību.
Datu struktūras nodrošina vienkāršu veidu, kā organizēt, izgūt, pārvaldīt un uzglabāt datus.
Šeit ir saraksts ar vajadzībām pēc datiem.
- Datu struktūras pārveidošana ir vienkārša.
- Tas prasa mazāk laika.
- Ietaupiet atmiņas vietu.
- Datu attēlošana ir vienkārša.
- Ērta piekļuve lielajai datu bāzei.
Masīvi:
Masīvs ir lineāra datu struktūra, un tā ir vienumu kolekcija, kas glabājas blakus esošās atmiņas vietās. Ideja ir vienā vietā glabāt vairākus viena veida vienumus. Tas ļauj apstrādāt lielu datu apjomu salīdzinoši īsā laika periodā. Pirmais masīva elements tiek indeksēts ar apakšindeksu 0. Masīvā ir iespējamas dažādas darbības, piemēram, meklēšana, kārtošana, ievietošana, pārvietošana, apgriešana un dzēšana.
kā pārbaudīt bloķētos numurus operētājsistēmā Android

Masīvs
Masīva īpašības:
Masīvam ir dažādas īpašības, kas ir šādas:
- Masīvi izmanto uz indeksu balstītu datu struktūru, kas palīdz viegli identificēt katru masīva elementu, izmantojot indeksu.
- Ja lietotājs vēlas saglabāt vairākas viena un tā paša datu tipa vērtības, masīvu var izmantot efektīvi.
- Masīvs var apstrādāt arī sarežģītas datu struktūras, glabājot datus divdimensiju masīvā.
- Masīvs tiek izmantots arī, lai ieviestu citas datu struktūras, piemēram, Stacks, Queues, Heaps, Hash tabulas utt.
- Meklēšanas procesu masīvā var veikt ļoti vienkārši.
Ar masīvu veiktās darbības:
- Inicializācija : masīvu var inicializēt ar vērtībām deklarēšanas laikā vai vēlāk, izmantojot piešķiršanas paziņojumu.
- Piekļuve elementiem: masīva elementiem var piekļūt, izmantojot to indeksu, kas sākas no 0 un palielinās līdz masīva lielumam mīnus viens.
- Elementu meklēšana : Masīvus var meklēt pēc noteikta elementa, izmantojot lineāro vai bināro meklēšanas algoritmus.
- Elementu šķirošana : masīva elementus var kārtot augošā vai dilstošā secībā, izmantojot tādus algoritmus kā burbuļu kārtošana, ievietošanas kārtošana vai ātrā kārtošana.
- Elementu ievietošana: Elementus var ievietot masīvā noteiktā vietā, taču šī darbība var būt laikietilpīga, jo ir jāpārvieto esošie elementi masīvā.
- Elementu dzēšana: Elementus var dzēst no masīva, pārvietojot elementus, kas nāk aiz tā, lai aizpildītu tukšumu.
- Elementu atjaunināšana: Masīva elementus var atjaunināt vai modificēt, piešķirot noteiktam indeksam jaunu vērtību.
- Šķērsošanas elementi: Masīva elementus var šķērsot secībā, katru elementu apmeklējot vienu reizi.
Šīs ir dažas no visbiežāk veiktajām operācijām ar masīviem. Izmantotās īpašās darbības un algoritmi var atšķirties atkarībā no problēmas prasībām un izmantotās programmēšanas valodas.
Masīva lietojumprogrammas:
Dažādas masīva lietojumprogrammas ir šādas:
- Masīvs tiek izmantots matricas uzdevumu risināšanā.
- Datu bāzes ierakstus realizē arī masīvs.
- Tas palīdz ieviest šķirošanas algoritmu.
- To izmanto arī, lai ieviestu citas datu struktūras, piemēram, Stacks, Queues, Heaps, Hash tabulas utt.
- CPU plānošanai var izmantot masīvu.
- Var izmantot kā uzmeklēšanas tabulu datoros.
- Masīvus var izmantot runas apstrādē, kur katrs runas signāls ir masīvs.
- Datora ekrāns tiek parādīts arī ar masīvu. Šeit mēs izmantojam daudzdimensiju masīvu.
- Masīvs tiek izmantots daudzās pārvaldības sistēmās, piemēram, bibliotēkā, studentos, parlamentā utt.
- Masīvs tiek izmantots tiešsaistes biļešu rezervēšanas sistēmā. Šajā masīvā tiek parādīti kontakti mobilajā tālrunī.
- Tādās spēlēs kā tiešsaistes šahs, kur spēlētājs var saglabāt savus iepriekšējos un pašreizējos gājienus. Tas norāda uz pozīcijas mājienu.
- Lai saglabātu attēlus noteiktā izmērā Android ierīcē Like 360*1200
Masīva reālās dzīves lietojumprogrammas:
- Masīvu bieži izmanto, lai saglabātu datus matemātiskiem aprēķiniem.
- To izmanto attēlu apstrādē.
- To izmanto arī ierakstu pārvaldībā.
- Grāmatu lapas ir arī reāli masīva piemēri.
- To izmanto arī kastīšu pasūtīšanai.
Vai vēlaties sākt darbu ar masīviem? Lai iegūtu labāko praksi, varat izmēģināt mūsu atlasītos rakstus un sarakstus.
- Ievads masīva datu struktūrā
- 50 populārākās masīvu kodēšanas problēmas intervijām
- Praktizējiet masīva problēmu vietnē techcodeview.com
Saistītais saraksts:
Saistītais saraksts ir lineāra datu struktūra, kurā elementi netiek glabāti blakus esošās atmiņas vietās. Saistītā saraksta elementi ir saistīti, izmantojot norādes, kā parādīts zemāk esošajā attēlā:
Saistīto sarakstu veidi:
- Atsevišķi saistīts saraksts
- Divkārši saistīts saraksts
- Apļveida saistīts saraksts
- Divkārši apļveida saiti saraksts

Saistītais saraksts
Saistītā saraksta īpašības:
Saistītajam sarakstam ir dažādas pazīmes, kas ir šādas:
- Saistītais saraksts izmanto papildu atmiņu, lai saglabātu saites.
- Saistītā saraksta inicializācijas laikā nav jāzina elementu lielums.
- Saistītie saraksti tiek izmantoti, lai ieviestu stekus, rindas, grafikus utt.
- Saistītā saraksta pirmo mezglu sauc par galvu.
- Nākamais pēdējā mezgla rādītājs vienmēr norāda uz NULL.
- Saistītajā sarakstā ievietošana un dzēšana ir vienkārša.
- Katrs saistītā saraksta mezgls sastāv no rādītāja/saites, kas ir nākamā mezgla adrese.
- Saistītie saraksti jebkurā brīdī var viegli sarukt vai palielināties.
Saistītajā sarakstā veiktās darbības:
Saistītais saraksts ir lineāra datu struktūra, kurā katrs mezgls satur vērtību un atsauci uz nākamo mezglu. Šeit ir dažas izplatītas darbības, kas tiek veiktas saistītajos sarakstos.
- Inicializācija: Saistīto sarakstu var inicializēt, izveidojot galveno mezglu ar atsauci uz pirmo mezglu. Katrs nākamais mezgls satur vērtību un atsauci uz nākamo mezglu.
- Elementu ievietošana: Elementus var ievietot pie galvas, astes vai noteiktā pozīcijā saistītajā sarakstā.
- Elementu dzēšana : Elementus var dzēst no saistītā saraksta, atjauninot iepriekšējā mezgla atsauci, lai norādītu uz nākamo mezglu, efektīvi noņemot pašreizējo mezglu no saraksta.
- Elementu meklēšana : Saistītajos sarakstos var meklēt konkrētu elementu, sākot no galvenā mezgla un sekojot atsaucēm uz nākamajiem mezgliem, līdz tiek atrasts vajadzīgais elements.
- Elementu atjaunināšana : Saistītā saraksta elementus var atjaunināt, mainot konkrēta mezgla vērtību.
- Šķērsošanas elementi: Saistītā saraksta elementus var šķērsot, sākot no galvenā mezgla un sekojot atsaucēm uz nākamajiem mezgliem, līdz tiek sasniegts saraksta beigas.
- Saistītā saraksta apvēršana : saistīto sarakstu var mainīt, atjauninot katra mezgla atsauces, lai tās norādītu uz iepriekšējo mezglu, nevis uz nākamo mezglu.
Šīs ir dažas no visbiežāk veiktajām darbībām saistītajos sarakstos. Izmantotās īpašās darbības un algoritmi var atšķirties atkarībā no problēmas prasībām un izmantotās programmēšanas valodas.
Saistītā saraksta lietojumprogrammas:
Saistīto sarakstu dažādas lietojumprogrammas ir šādas:
- Saistītie saraksti tiek izmantoti, lai ieviestu stekus, rindas, grafikus utt.
- Saistītie saraksti tiek izmantoti, lai veiktu aritmētiskās darbības ar gariem veseliem skaitļiem.
- To izmanto retu matricu attēlošanai.
- To izmanto saistīto failu piešķiršanā.
- Tas palīdz atmiņas pārvaldībā.
- To izmanto polinomu manipulācijas attēlojumā, kur katrs polinoma termins apzīmē mezglu saistītajā sarakstā.
- Saistītie saraksti tiek izmantoti attēlu konteineru parādīšanai. Lietotāji var apmeklēt iepriekšējos, pašreizējos un nākamos attēlus.
- Tie tiek izmantoti, lai saglabātu apmeklētās lapas vēsturi.
- Tos izmanto, lai veiktu atsaukšanas darbības.
- Saistītie tiek izmantoti programmatūras izstrādē, kur tie norāda pareizo taga sintaksi.
- Saistītie saraksti tiek izmantoti, lai parādītu sociālo mediju plūsmas.
Saistītā saraksta reālās dzīves lietojumprogrammas:
- Saistīts saraksts tiek izmantots Round-Robin plānošanā, lai sekotu līdzi gājienam vairāku spēlētāju spēlēs.
- To izmanto attēlu skatītājā. Iepriekšējie un nākamie attēli ir saistīti, un tādējādi tiem var piekļūt, izmantojot iepriekšējās un nākamās pogas.
- Mūzikas atskaņošanas sarakstā dziesmas ir saistītas ar iepriekšējo un nākamo dziesmu.
Vai vēlaties sākt darbu ar saistīto sarakstu? Lai iegūtu labāko praksi, varat izmēģināt mūsu atlasītos rakstus un sarakstus.
- Saistītā saraksta datu struktūras ievads
- 20 populārākie saistītie intervijas jautājumi
- Praktizējiet saistīto sarakstu problēmu vietnē techcodeview.com
Kaudze:
Stack ir lineāra datu struktūra, kas atbilst noteiktai secībai, kādā tiek veiktas darbības. Pasūtījums ir LIFO (pēdējais pirmais ārā) . Datu ievadīšana un izgūšana ir iespējama tikai no viena gala. Datu ievadīšanu un izgūšanu sauc arī par push un pop darbību kaudzē. Kaudzē ir iespējamas dažādas darbības, piemēram, kaudzes apgriešana, izmantojot rekursiju, kārtošana, kaudzes vidējā elementa dzēšana utt.

Kaudze
Stacka īpašības:
Stackam ir dažādas īpašības, kas ir šādas:
- Stack tiek izmantots daudzos dažādos algoritmos, piemēram, Hanojas tornī, koku šķērsošanā, rekursijā utt.
- Stack tiek ieviests, izmantojot masīvu vai saistīto sarakstu.
- Tas seko operācijai Last In First Out, t.i., elements, kas ievietots pirmais, tiks parādīts pēdējais un otrādi.
- Ievietošana un dzēšana tiek veikta vienā galā, t.i., no kaudzes augšdaļas.
- Ja stekā atvēlētā vieta ir pilna un kāds mēģina pievienot vairāk elementu, tas novedīs pie steka pārpildes.
Stack pielietojumi:
Dažādas Stack lietojumprogrammas ir šādas:
- Stack datu struktūra tiek izmantota aritmētisko izteiksmju novērtēšanā un pārveidošanā.
- To izmanto iekavu pārbaudei.
- Apgriežot virkni, tiek izmantota arī kaudze.
- Stack tiek izmantots atmiņas pārvaldībā.
- To izmanto arī funkciju zvanu apstrādei.
- Kaudze tiek izmantota, lai pārvērstu izteiksmes no infix uz postfix.
- Kaudze tiek izmantota, lai tekstapstrādes programmās veiktu atsaukšanas, kā arī pārtaisīšanas darbības.
- Kaudze tiek izmantota virtuālajās mašīnās, piemēram, JVM.
- Kaudzīte tiek izmantota multivides atskaņotājos. Noder, lai atskaņotu nākamo un iepriekšējo dziesmu.
- Stacks tiek izmantots rekursijas operācijās.
Darbība veikta uz skursteņa ;
Stacks ir lineāra datu struktūra, kurā tiek īstenots LIFO princips. Šeit ir dažas izplatītas darbības, kas tiek veiktas ar skursteņiem:
- Spiediet : Elementus var uzspiest kaudzes augšpusē, pievienojot jaunu elementu kaudzes augšpusē.
- Pop : augšējo elementu var noņemt no kaudzes, veicot uznirstošo darbību, efektīvi noņemot pēdējo elementu, kas tika uzstumts uz kaudzītes.
- Ielūkoties: Augšējo elementu var pārbaudīt, neizņemot to no kaudzes, izmantojot apskates darbību.
- Ir tukšs : var veikt pārbaudi, lai noteiktu, vai kaudze ir tukša.
- Izmērs : elementu skaitu kaudzē var noteikt, izmantojot lieluma darbību.
Šīs ir dažas no visbiežāk veiktajām darbībām ar skursteņiem. Izmantotās īpašās darbības un algoritmi var atšķirties atkarībā no problēmas prasībām un izmantotās programmēšanas valodas. Stackus parasti izmanto lietojumprogrammās, piemēram, izteiksmju novērtēšanā, funkciju izsaukuma steku ieviešanā datorprogrammās un daudzās citās.
Stack reālās dzīves lietojumprogrammas:
- Reāls kaudzes piemērs ir ēšanas šķīvju slānis, kas novietots viens virs otra. Noņemot šķīvi no kaudzes, varat to paņemt līdz kaudzes augšdaļai. Bet tieši šī plāksne tika pievienota kaudzē pavisam nesen. Ja vēlaties, lai plāksne būtu kaudzes apakšā, jums ir jānoņem visas tās augšdaļas plāksnes, lai to sasniegtu.
- Pārlūkprogrammas izmanto steku datu struktūras, lai izsekotu iepriekš apmeklētajām vietnēm.
- Zvanu žurnāls mobilajā ierīcē arī izmanto steku datu struktūru.
Vai vēlaties sākt darbu ar Stack? Lai iegūtu labāko praksi, varat izmēģināt mūsu atlasītos rakstus un sarakstus.
concat virknes java
- Praktizējiet Stack problēmu vietnē techcodeview.com
Rinda:
Rinda ir lineāra datu struktūra, kas atbilst noteiktai secībai, kādā tiek veiktas darbības. Pasūtījums ir First In First Out (FIFO) i., vispirms tiks piekļūts datu vienumam, kas saglabāts pirmais. Šajā gadījumā datu ievadīšana un izgūšana netiek veikta tikai no viena gala. Rindas piemērs ir jebkura resursa patērētāju rinda, kurā vispirms tiek apkalpots patērētājs, kurš bija pirmais. Rindā tiek veiktas dažādas darbības, piemēram, rindas apgriešana (ar vai bez rekursijas izmantošanas), rindas pirmo K elementu apgriešana utt. Dažas rindā veicamās pamatoperācijas ir rinda, rinda, priekšpuse, aizmugure utt.
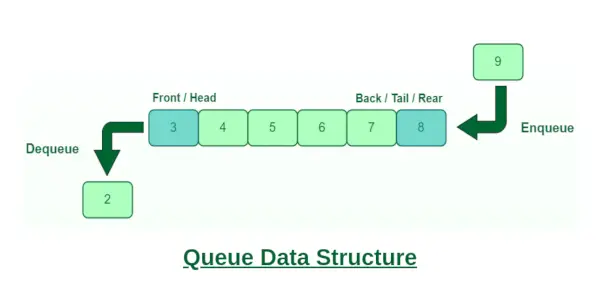
Rinda
Rindas raksturojums:
Rindai ir dažādas īpašības, kas ir šādas:
- Rinda ir FIFO (First In First Out) struktūra.
- Lai noņemtu rindas pēdējo elementu, ir jānoņem visi elementi, kas rindā ievietoti pirms jaunā elementa.
- Rinda ir sakārtots līdzīgu datu tipu elementu saraksts.
Rindas lietojumprogrammas:
Dažādas rindas lietojumprogrammas ir šādas:
- Rinda tiek izmantota vietnes trafika apstrādei.
- Tas palīdz saglabāt atskaņošanas sarakstu multivides atskaņotājos.
- Rinda tiek izmantota operētājsistēmās pārtraukumu apstrādei.
- Tas palīdz apkalpot pieprasījumus vienā koplietotā resursā, piemēram, printerī, CPU uzdevumu plānošanā utt.
- To izmanto asinhronai datu pārsūtīšanai, piem. caurules, failu IO un kontaktligzdas.
- Rindas tiek izmantotas darbu plānošanai operētājsistēmā.
- Sociālajos medijos vairāku fotoattēlu vai videoklipu augšupielādei tiek izmantota rinda.
- E-pasta nosūtīšanai tiek izmantota rinda datu struktūra.
- Lai vienā laikā apstrādātu vietnes trafiku, tiek izmantotas rindas.
- Operētājsistēmā Windows, lai pārslēgtu vairākas lietojumprogrammas.
Operācija veikta rindā:
Rinda ir lineāra datu struktūra, kas īsteno FIFO (First-In-First-Out) principu. Tālāk ir norādītas dažas biežāk veiktās darbības ar rindām.
- Rindā : Elementus var pievienot rindas aizmugurē, pievienojot jaunu elementu rindas beigās.
- Attiecīgi : priekšējo elementu var noņemt no rindas, veicot rindas noņemšanas darbību, efektīvi noņemot pirmo rindai pievienoto elementu.
- Palūrēt : priekšējo elementu var pārbaudīt, nenoņemot to no rindas, izmantojot apskates darbību.
- Ir tukšs : var veikt pārbaudi, lai noteiktu, vai rinda ir tukša.
- Izmērs : Elementu skaitu rindā var noteikt, izmantojot lieluma darbību.
Šīs ir dažas no visizplatītākajām operācijām, kas tiek veiktas rindās. Izmantotās īpašās darbības un algoritmi var atšķirties atkarībā no problēmas prasībām un izmantotās programmēšanas valodas. Rindas parasti izmanto lietojumprogrammās, piemēram, uzdevumu plānošanā, saziņas pārvaldībā starp procesiem un daudzās citās.
Rindas reālās dzīves lietojumprogrammas:
- Reāls rindas piemērs ir vienas joslas vienvirziena ceļš, kurā pirmais izbrauc transportlīdzeklis, kurš iebrauc pirmais.
- Reālāku piemēru var redzēt rindā pie biļešu logiem.
- Arī kases rinda veikalā ir rindas piemērs.
- Cilvēki uz eskalatora
Vai vēlaties sākt darbu ar rindu? Lai iegūtu labāko praksi, varat izmēģināt mūsu atlasītos rakstus un sarakstus.
- Praktizējiet rindas problēmu vietnē techcodeview.com
Koks:
Koks ir nelineāra un hierarhiska datu struktūra, kurā elementi ir sakārtoti kokam līdzīgā struktūrā. Kokā augšējo mezglu sauc par saknes mezglu. Katrs mezgls satur dažus datus, un dati var būt jebkura veida. Tas sastāv no centrālā mezgla, strukturālajiem mezgliem un apakšmezgliem, kas ir savienoti caur malām. Dažādas koka datu struktūras ļauj ātrāk un vienkāršāk piekļūt datiem, jo tā ir nelineāra datu struktūra. Kokam ir dažādas terminoloģijas, piemēram, mezgls, sakne, mala, koka augstums, koka pakāpe utt.
Ir dažādi koka veida veidi
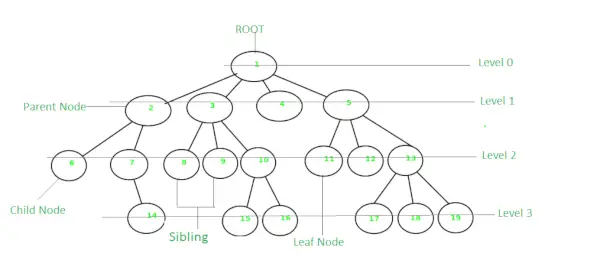
Koks
Koka īpašības:
Kokam ir dažādas īpašības, kas ir šādas:
- Koku sauc arī par rekursīvo datu struktūru.
- Kokā saknes augstumu var definēt kā garāko ceļu no saknes mezgla līdz lapas mezglam.
- Kokā var arī aprēķināt dziļumu no augšas līdz jebkuram mezglam. Saknes mezgla dziļums ir 0.
Koka pielietojumi:
Dažādi Tree pielietojumi ir šādi:
- Kaudze ir koka datu struktūra, kas tiek ieviesta, izmantojot masīvus, un tiek izmantota prioritāro rindu ieviešanai.
- B-Tree un B+ Tree tiek izmantoti indeksēšanas ieviešanai datu bāzēs.
- Sintakses koks palīdz skenēt, analizēt, ģenerēt kodu un novērtēt aritmētiskās izteiksmes kompilatora dizainā.
- K-D koks ir telpas sadalīšanas koks, ko izmanto, lai organizētu punktus K-dimensijas telpā.
- Datortīklu maršrutētājos tiek izmantoti aptverošie koki.
Operācija kokā:
Koks ir nelineāra datu struktūra, kas sastāv no mezgliem, kas savienoti ar malām. Šeit ir dažas izplatītas darbības, ko veic ar kokiem:
- Ievietošana : kokam var pievienot jaunus mezglus, lai izveidotu jaunu zaru vai palielinātu koka augstumu.
- Dzēšana : mezglus var noņemt no koka, atjauninot vecākmezgla atsauces, lai noņemtu atsauci uz pašreizējo mezglu.
- Meklēt : Elementus var meklēt kokā, sākot no saknes mezgla un šķērsojot koku, pamatojoties uz pašreizējā mezgla vērtību, līdz tiek atrasts vēlamais mezgls.
- Šķērsošana : Elementus kokā var šķērsot vairākos dažādos veidos, tostarp pasūtījuma, priekšpasūtīšanas un pēcpasūtīšanas šķērsošanas.
- Augstums : Koka augstumu var noteikt, saskaitot malu skaitu no saknes mezgla līdz tālākajam lapas mezglam.
- Dziļums : mezgla dziļumu var noteikt, saskaitot malu skaitu no saknes mezgla līdz pašreizējam mezglam.
- Balansēšana : Koku var līdzsvarot, lai nodrošinātu, ka koka augstums tiek samazināts līdz minimumam un mezglu sadalījums ir pēc iespējas vienmērīgāks.
Šīs ir dažas no visbiežāk veiktajām darbībām ar kokiem. Izmantotās īpašās darbības un algoritmi var atšķirties atkarībā no problēmas prasībām un izmantotās programmēšanas valodas. Koki parasti tiek izmantoti tādās lietojumprogrammās kā hierarhisku datu meklēšana, šķirošana un glabāšana.
Koka pielietojumi reālajā dzīvē:
- Reālajā dzīvē koka datu struktūra palīdz spēļu izstrādē.
- Tas arī palīdz indeksēt datu bāzēs.
- Lēmumu koks ir efektīvs mašīnmācības rīks, ko parasti izmanto lēmumu analīzē. Tam ir blokshēmai līdzīga struktūra, kas palīdz izprast datus.
- Domēna nosaukumu serveris izmanto arī koka datu struktūru.
- Visizplatītākais koka izmantošanas gadījums ir jebkura sociālā tīkla vietne.
Vai vēlaties sākt darbu ar Tree? Lai iegūtu labāko praksi, varat izmēģināt mūsu atlasītos rakstus un sarakstus.
- 50 populārākie koka intervijas jautājumi
- Prakses koka problēma vietnē techcodeview.com
Grafiks:
Grafiks ir nelineāra datu struktūra, kas sastāv no virsotnēm (vai mezgliem) un malām. Tas sastāv no ierobežotas virsotņu kopas un malu kopas, kas savieno mezglu pāri. Grafiku izmanto, lai atrisinātu vissarežģītākās un sarežģītākās programmēšanas problēmas. Tam ir dažādas terminoloģijas, kas ir ceļš, grāds, blakus esošās virsotnes, savienotie komponenti utt.
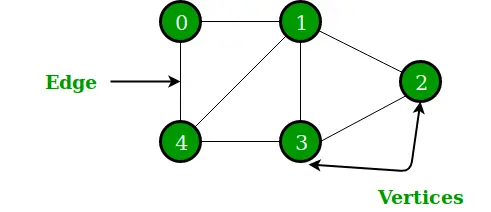
Grafiks
Grafika raksturojums:
Diagrammai ir dažādas īpašības, kas ir šādas:
- Maksimālais attālums no virsotnes līdz visām pārējām virsotnēm tiek uzskatīts par šīs virsotnes ekscentriskumu.
- Virsotne ar minimālo ekscentriskumu tiek uzskatīta par grafika centrālo punktu.
- Ekscentricitātes minimālā vērtība no visām virsotnēm tiek uzskatīta par savienotā grafika rādiusu.
Grafika pielietojumi:
Dažādi grafiku lietojumi ir šādi:
- Grafiku izmanto, lai attēlotu aprēķinu plūsmu.
- To izmanto grafiku modelēšanā.
- Operētājsistēma izmanto resursu piešķiršanas grafiku.
- Izmanto arī globālajā tīmeklī, kur tīmekļa lapas attēlo mezglus.
Darbība, kas veikta grafikā:
Grafiks ir nelineāra datu struktūra, kas sastāv no mezgliem un malām. Šeit ir dažas izplatītas darbības, kas tiek veiktas ar grafikiem:
- Pievienot virsotni: Grafam var pievienot jaunas virsotnes, lai attēlotu jaunu mezglu.
- Pievienot malu: Starp virsotnēm var pievienot malas, lai attēlotu attiecības starp mezgliem.
- Noņemiet virsotni : Virsotnes var noņemt no grafika, atjauninot blakus esošo virsotņu atsauces, lai noņemtu atsauci uz pašreizējo virsotni.
- Noņemiet Edge : malas var noņemt, atjauninot blakus esošo virsotņu atsauces, lai noņemtu atsauci uz pašreizējo malu.
- Dziļuma pirmā meklēšana (DFS) : Grafiku var šķērsot, izmantojot meklēšanu pēc dziļuma, apmeklējot virsotnes vispirms dziļumā.
- B readth-First Search (BFS): Grafiku var šķērsot, izmantojot meklēšanu pēc platuma, virsotnes apmeklējot pēc platuma.
- Īsākais ceļš: Īsāko ceļu starp divām virsotnēm var noteikt, izmantojot tādus algoritmus kā Dijkstra algoritms vai A* algoritms.
- Savienotie komponenti : Grafa savienotās sastāvdaļas var noteikt, atrodot virsotņu kopas, kas ir savienotas viena ar otru, bet nav savienotas ar citām grafa virsotnēm.
- Cikla noteikšana : Ciklus diagrammā var noteikt, pārbaudot aizmugurējās malas, veicot meklēšanu pēc dziļuma.
Šīs ir dažas no visizplatītākajām darbībām, kas tiek veiktas ar grafikiem. Izmantotās īpašās darbības un algoritmi var atšķirties atkarībā no problēmas prasībām un izmantotās programmēšanas valodas. Grafikus parasti izmanto tādās lietojumprogrammās kā datortīkli, sociālie tīkli un maršrutēšanas problēmas.
Grafika reālās dzīves lietojumi:
- Viens no visizplatītākajiem grafikas piemēriem reālajā pasaulē ir Google Maps, kur pilsētas atrodas kā virsotnes un ceļi, kas savieno šīs virsotnes, atrodas kā grafika malas.
- Sociālais tīkls ir arī viens reāls diagrammas piemērs, kur katrs tīklā esošais cilvēks ir mezgls, un visas viņu draudzības tīklā ir diagrammas malas.
- Grafiku izmanto arī molekulu pētīšanai fizikā un ķīmijā.
Vai vēlaties sākt darbu ar Graph? Lai iegūtu labāko praksi, varat izmēģināt mūsu atlasītos rakstus un sarakstus.
kā pārbaudīt monitora ekrāna izmēru
- Ievads grafika datu struktūrā
- 50 populārākie diagrammas intervijas jautājumi
- Praktizējiet Graph problēmu vietnē techcodeview.com
Datu struktūras priekšrocības:
- Uzlabota datu organizēšanas un uzglabāšanas efektivitāte.
- Ātrāka datu izguve un manipulācijas.
- Atvieglo algoritmu izstrādi sarežģītu problēmu risināšanai.
- Atvieglo datu atjaunināšanas un uzturēšanas uzdevumu.
- Nodrošina labāku izpratni par attiecībām starp datu elementiem.
Datu struktūras trūkums:
- Palielinātas skaitļošanas un atmiņas izmaksas.
- Grūtības sarežģītu datu struktūru projektēšanā un ieviešanā.
- Ierobežota mērogojamība un elastība.
- Atkļūdošanas un testēšanas sarežģītība.
- Grūtības mainīt esošās datu struktūras.
Atsauce:
Datu struktūras var atrast dažādās datorzinātņu mācību grāmatās un tiešsaistes resursos. Daži populāri teksti ietver:
- Tomasa H. Kormena, Čārlza E. Leizersona, Ronalda L. Rivesta un Kliforda Steina ievadu algoritmos.
- Datu struktūru un algoritmu analīze Java valodā, Marks Allens Veiss.
- Stīvena S. Skienas algoritmu izstrādes rokasgrāmata.
- Tiešsaistes resursi, piemēram, Coursera, Udemy un Khan Academy, piedāvā arī kursus par datu struktūrām un algoritmiem.
Secinājums
Lai gan šīs ir visplašāk zināmās un lietotās datu struktūras, ir arī daži citi datu struktūru veidi, kas tiek izmantoti datorzinātnēs, piemēram, uz politiku balstītas datu struktūras u.c. Taču neatkarīgi no izvēlētās datu struktūras katrai no tām ir savas priekšrocības un trūkumi, par kuriem nezinot, nepareiza veida datu struktūras izvēle var būt ļoti dārga. Tāpēc ir ļoti svarīgi izprast situācijas nepieciešamību un pēc tam izlemt, kāda veida datu struktūra ir vispiemērotākā šim darbam.
