Tradicionālo bināro meklēšanas koku ierobežojumi var būt neapmierinoši. Iepazīstieties ar B-Tree — daudzpusīgu datu struktūru, kas var viegli apstrādāt milzīgus datu apjomus. Runājot par liela datu apjoma uzglabāšanu un meklēšanu, tradicionālie binārie meklēšanas koki var kļūt nepraktiski to sliktās veiktspējas un lielā atmiņas lietojuma dēļ. B-Trees, kas pazīstams arī kā B-Tree vai Balanced Tree, ir pašbalansējoša koka veids, kas tika īpaši izstrādāts, lai pārvarētu šos ierobežojumus.
Atšķirībā no tradicionālajiem binārajiem meklēšanas kokiem, B-Trees raksturo liels skaits atslēgu, ko tie var saglabāt vienā mezglā, tāpēc tos sauc arī par lieliem atslēgu kokiem. Katrs B-koka mezgls var saturēt vairākas atslēgas, kas ļauj kokam iegūt lielāku sazarojuma koeficientu un līdz ar to arī zemāku augstumu. Šis zemais augstums samazina diska ievades/izvades apjomu, kā rezultātā tiek veiktas ātrākas meklēšanas un ievietošanas darbības. B-Trees ir īpaši labi piemēroti uzglabāšanas sistēmām, kurām ir lēna, apjomīga piekļuve datiem, piemēram, cietajiem diskiem, zibatmiņai un CD-ROM.
B-Trees saglabā līdzsvaru, nodrošinot, ka katram mezglam ir minimāls atslēgu skaits, tāpēc koks vienmēr ir līdzsvarots. Šis līdzsvars garantē, ka laika sarežģītība tādām darbībām kā ievietošana, dzēšana un meklēšana vienmēr ir O(log n) neatkarīgi no koka sākotnējās formas.
B koka laika sarežģītība:
| kungs Nr. | Algoritms | Laika sarežģītība |
|---|---|---|
| 1. | Meklēt | O(log n) |
| 2. | Ievietot | O(log n) |
| 3. | Dzēst | O(log n) |
Piezīme: n ir kopējais elementu skaits B-kokā
kas ir f5 uz tastatūras
B-Tree īpašības:
- Visas lapas atrodas vienā līmenī.
- B-koks tiek definēts ar terminu minimālā pakāpe ' t ‘. Vērtība ' t 'atkarīgs no diska bloka lieluma.
- Katrā mezglā, izņemot sakni, jābūt vismaz t-1 atslēgām. Saknē var būt vismaz 1 taustiņu.
- Visos mezglos (ieskaitot saknes) var būt ne vairāk kā ( 2*t – 1 ) atslēgas.
- Mezgla bērnu skaits ir vienāds ar tajā esošo atslēgu skaitu plus 1 .
- Visas mezgla atslēgas tiek sakārtotas augošā secībā. Bērns starp divām atslēgām k1 un k2 satur visas atslēgas diapazonā no k1 un k2 .
- B-Tree aug un saraujas no saknes, kas ir atšķirībā no Binary Search Tree. Binārie meklēšanas koki aug uz leju un arī saraujas no lejas.
- Tāpat kā citiem līdzsvarotiem binārās meklēšanas kokiem, meklēšanas, ievietošanas un dzēšanas laika sarežģītība ir O(log n).
- Mezgla ievietošana B-kokā notiek tikai lapu mezglā.
Tālāk ir sniegts B-koka piemērs ar minimālo pasūtījumu 5
Piezīme: ka praktiskajos B-Trees minimālā pasūtījuma vērtība ir daudz lielāka par 5.

Iepriekš redzamajā diagrammā redzams, ka visi lapu mezgli atrodas vienā līmenī un visām lapām, kurām nav tukšu apakškoku, un tām ir par vienu atslēgu mazāks nekā to bērnu skaits.
Interesanti fakti par B-kokiem:
- Minimālais B koka augstums, kas var pastāvēt ar n mezglu skaitu un m ir maksimālais mezgla bērnu skaits, kas var būt:
- Maksimālais B koka augstums, kas var pastāvēt ar n mezglu skaitu un t ir minimālais bērnu skaits, kas var būt mezglam, kas nav saknes mezgls, ir:
un
Braukšana pa B koku:
Traversal ir arī līdzīgs Inorder traversal of Binary Tree. Mēs sākam no vistālāk kreisā bērna, rekursīvi izdrukājam vistālāk kreiso bērnu, pēc tam atkārtojam to pašu darbību pārējiem bērniem un atslēgām. Beigās rekursīvi izdrukājiet vislabāko bērnu.
javascript cilpai
Meklēšanas darbība B-Tree:
Meklēšana ir līdzīga meklēšanai binārajā meklēšanas kokā. Lai meklējamā atslēga ir k.
- Sāciet no saknes un rekursīvi virzieties uz leju.
- Par katru apmeklēto ne-lapu mezglu,
- Ja mezglam ir atslēga, mēs vienkārši atgriežam mezglu.
- Pretējā gadījumā mēs atgriežamies līdz atbilstošajam mezgla bērnam (bērnam, kas atrodas tieši pirms pirmās lielākās atslēgas).
- Ja sasniedzam lapas mezglu un lapas mezglā neatrodam k, atgrieziet NULL.
B-koka meklēšana ir līdzīga binārā koka meklēšanai. Algoritms ir līdzīgs un iet ar rekursiju. Katrā līmenī meklēšana tiek optimizēta tā, it kā atslēgas vērtība neatrastos vecāka diapazonā, tad atslēga atrodas citā atzarā. Tā kā šīs vērtības ierobežo meklēšanu, tās sauc arī par ierobežojošām vērtībām vai atdalīšanas vērtībām. Ja mēs sasniedzam lapas mezglu un neatrodam vajadzīgo atslēgu, tas parādīs NULL.
Algoritms elementa meklēšanai B-kokā:
C++
struct> Node {> >int> n;> >int> key[MAX_KEYS];> >Node* child[MAX_CHILDREN];> >bool> leaf;> };> Node* BtreeSearch(Node* x,>int> k) {> >int> i = 0;> >while> (i n && k>x->key[i]) {> >i++;> >}> >if> (i n && k == x->taustiņš [i]) {> >return> x;> >}> >if> (x->lapa) {> >return> nullptr;> >}> >return> BtreeSearch(x->bērns [i], k);> }> |
>
>
C
BtreeSearch(x, k)> >i = 1> > >// n[x] means number of keys in x node> >while> i ? n[x] and k ? keyi[x]> >do> i = i + 1> >if> i n[x] and k = keyi[x]> >then>return> (x, i)> >if> leaf [x]> >then>return> NIL> >else> >return> BtreeSearch(ci[x], k)> |
>
>
Java
class> Node {> >int> n;> >int>[] key =>new> int>[MAX_KEYS];> >Node[] child =>new> Node[MAX_CHILDREN];> >boolean> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i =>0>;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Python3
class> Node:> >def> __init__(>self>):> >self>.n>=> 0> >self>.key>=> [>0>]>*> MAX_KEYS> >self>.child>=> [>None>]>*> MAX_CHILDREN> >self>.leaf>=> True> def> BtreeSearch(x, k):> >i>=> 0> >while> i and k>= x.atslēga[i]: i += 1, ja i un k == x.atslēga[i]: atgriež x, ja x.leaf: atgriež Nav atgriež BtreeSearch(x.child[i], k)> |
>
>
C#
class> Node {> >public> int> n;> >public> int>[] key =>new> int>[MAX_KEYS];> >public> Node[] child =>new> Node[MAX_CHILDREN];> >public> bool> leaf;> }> Node BtreeSearch(Node x,>int> k) {> >int> i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Javascript
// Define a Node class with properties n, key, child, and leaf> class Node {> >constructor() {> >this>.n = 0;> >this>.key =>new> Array(MAX_KEYS);> >this>.child =>new> Array(MAX_CHILDREN);> >this>.leaf =>false>;> >}> }> // Define a function BtreeSearch that takes in a Node object x and an integer k> function> BtreeSearch(x, k) {> >let i = 0;> >while> (i = x.key[i]) {> >i++;> >}> >if> (i return x; } if (x.leaf) { return null; } return BtreeSearch(x.child[i], k); }> |
>
>
Piemēri:
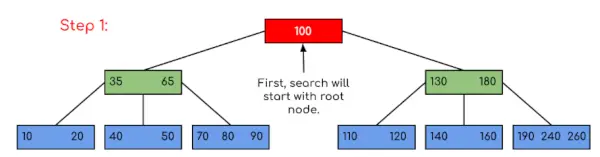
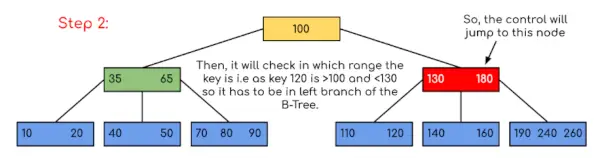
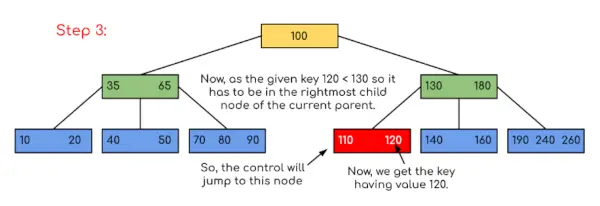
Ievade: Meklēt 120 dotajā B-Kokā.
Risinājums:
javascript virknes apgriešana
Šajā piemērā mēs redzam, ka mūsu meklēšana tika samazināta, tikai ierobežojot iespējas, kur varētu būt atslēga, kas satur vērtību. Līdzīgi, ja iepriekš minētajā piemērā mums ir jāmeklē 180, vadīkla apstāsies pie 2. darbības, jo programma atklās, ka atslēga 180 atrodas pašreizējā mezglā. Un līdzīgi, ja ir jāmeklē 90, tad kā 90 <100, tas automātiski pāriet uz kreiso apakškoku, un tāpēc vadības plūsma notiks līdzīgi, kā parādīts iepriekš minētajā piemērā.
kā noņemt atlasi programmā gimp
Tālāk ir aprakstīta iepriekš minētās pieejas īstenošana.
C++
// C++ implementation of search() and traverse() methods> #include> using> namespace> std;> // A BTree node> class> BTreeNode {> >int>* keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode** C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> public>:> >BTreeNode(>int> _t,>bool> _leaf);>// Constructor> >// A function to traverse all nodes in a subtree rooted> >// with this node> >void> traverse();> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode*> >search(>int> k);>// returns NULL if k is not present.> >// Make the BTree friend of this so that we can access> >// private members of this class in BTree functions> >friend> class> BTree;> };> // A BTree> class> BTree {> >BTreeNode* root;>// Pointer to root node> >int> t;>// Minimum degree> public>:> >// Constructor (Initializes tree as empty)> >BTree(>int> _t)> >{> >root = NULL;> >t = _t;> >}> >// function to traverse the tree> >void> traverse()> >{> >if> (root != NULL)> >root->traverse();> >}> >// function to search a key in this tree> >BTreeNode* search(>int> k)> >{> >return> (root == NULL) ? NULL : root->meklēt(k);> >}> };> // Constructor for BTreeNode class> BTreeNode::BTreeNode(>int> _t,>bool> _leaf)> {> >// Copy the given minimum degree and leaf property> >t = _t;> >leaf = _leaf;> >// Allocate memory for maximum number of possible keys> >// and child pointers> >keys =>new> int>[2 * t - 1];> >C =>new> BTreeNode*[2 * t];> >// Initialize the number of keys as 0> >n = 0;> }> // Function to traverse all nodes in a subtree rooted with> // this node> void> BTreeNode::traverse()> {> >// There are n keys and n+1 children, traverse through n> >// keys and first n children> >int> i;> >for> (i = 0; i // If this is not leaf, then before printing key[i], // traverse the subtree rooted with child C[i]. if (leaf == false) C[i]->traversa(); cout<< ' ' << keys[i]; } // Print the subtree rooted with last child if (leaf == false) C[i]->traversa(); } // Funkcija, lai meklētu taustiņu k apakškokā, kas sakņojas ar šo mezglu BTreeNode* BTreeNode::search(int k) { // Atrast pirmo atslēgu, kas ir lielāka vai vienāda ar k int i = 0; while (i taustiņi[i]) i++; // Ja atrastā atslēga ir vienāda ar k, atgriež šo mezglu if (keys[i] == k) atgriež šo; // Ja atslēga šeit nav atrasta un šis ir lapas mezgls if (leaf == true) return NULL; // Dodieties uz atbilstošo bērnu atgriešanu C[i]->search(k); }> |
>
>
Java
// Java program to illustrate the sum of two numbers> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >System.out.println();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >boolean> >leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>boolean> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[>2> * t ->1>];> >this>.C =>new> BTreeNode[>2> * t];> >this>.n =>0>;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i =>0>;> >for> (i =>0>; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >System.out.print(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i =>0>;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> |
>
>
Python3
# Create a node> class> BTreeNode:> >def> __init__(>self>, leaf>=>False>):> >self>.leaf>=> leaf> >self>.keys>=> []> >self>.child>=> []> # Tree> class> BTree:> >def> __init__(>self>, t):> >self>.root>=> BTreeNode(>True>)> >self>.t>=> t> ># Insert node> >def> insert(>self>, k):> >root>=> self>.root> >if> len>(root.keys)>=>=> (>2> *> self>.t)>-> 1>:> >temp>=> BTreeNode()> >self>.root>=> temp> >temp.child.insert(>0>, root)> >self>.split_child(temp,>0>)> >self>.insert_non_full(temp, k)> >else>:> >self>.insert_non_full(root, k)> ># Insert nonfull> >def> insert_non_full(>self>, x, k):> >i>=> len>(x.keys)>-> 1> >if> x.leaf:> >x.keys.append((>None>,>None>))> >while> i>>> and> k[>0>] 0]: x.keys[i + 1] = x.keys[i] i -= 1 x.keys[i + 1] = k else: while i>= 0 un k[0] 0]: i -= 1 i += 1, ja len(x.child[i].keys) == (2 * self.t) - 1: self.split_child(x, i) if k[0]> x.keys[i][0]: i += 1 self.insert_non_full(x.child[i], k) # Sadaliet bērnu def split_child(self, x, i): t = self .t y = x.child[i] z = BTreeNode(y.leaf) x.child.insert(i + 1, z) x.keys.insert(i, y.keys[t - 1]) z.keys = y.keys[t: (2 * t) - 1] y.keys = y.keys[0: t - 1] ja nav y.leaf: z.child = y.child[t: 2 * t] y. bērns = y.bērns[0: t - 1] # Drukāt koku def print_tree(self, x, l=0): print('Level ', l, ' ', len(x.keys), end=':') for i in x.keys: print(i, end=' ') print() l += 1 if len(x.child)> 0: for i in x.child: self.print_tree(i, l) # Meklēšanas atslēga kokā def search_key(self, k, x=None): ja x nav Nav: i = 0 kamēr i |
>
>
C#
// C# program to illustrate the sum of two numbers> using> System;> // A BTree> class> Btree {> >public> BTreeNode root;>// Pointer to root node> >public> int> t;>// Minimum degree> >// Constructor (Initializes tree as empty)> >Btree(>int> t)> >{> >this>.root =>null>;> >this>.t = t;> >}> >// function to traverse the tree> >public> void> traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >Console.WriteLine();> >}> >// function to search a key in this tree> >public> BTreeNode search(>int> k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> }> // A BTree node> class> BTreeNode {> >int>[] keys;>// An array of keys> >int> t;>// Minimum degree (defines the range for number> >// of keys)> >BTreeNode[] C;>// An array of child pointers> >int> n;>// Current number of keys> >bool> leaf;>// Is true when node is leaf. Otherwise false> >// Constructor> >BTreeNode(>int> t,>bool> leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> int>[2 * t - 1];> >this>.C =>new> BTreeNode[2 * t];> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted> >// with this node> >public> void> traverse()> >{> >// There are n keys and n+1 children, traverse> >// through n keys and first n children> >int> i = 0;> >for> (i = 0; i <>this>.n; i++) {> >// If this is not leaf, then before printing> >// key[i], traverse the subtree rooted with> >// child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >Console.Write(keys[i] +>' '>);> >}> >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> >// A function to search a key in the subtree rooted with> >// this node.> >public> BTreeNode search(>int> k)> >{>// returns NULL if k is not present.> >// Find the first key greater than or equal to k> >int> i = 0;> >while> (i keys[i])> >i++;> >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> >// If the key is not found here and this is a leaf> >// node> >if> (leaf ==>true>)> >return> null>;> >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by Rajput-Ji> |
>
>
Javascript
// Javascript program to illustrate the sum of two numbers> // A BTree> class Btree> {> >// Constructor (Initializes tree as empty)> >constructor(t)> >{> >this>.root =>null>;> >this>.t = t;> >}> > >// function to traverse the tree> >traverse()> >{> >if> (>this>.root !=>null>)> >this>.root.traverse();> >document.write(>' '>);> >}> > >// function to search a key in this tree> >search(k)> >{> >if> (>this>.root ==>null>)> >return> null>;> >else> >return> this>.root.search(k);> >}> > }> // A BTree node> class BTreeNode> {> >// Constructor> >constructor(t,leaf)> >{> >this>.t = t;> >this>.leaf = leaf;> >this>.keys =>new> Array(2 * t - 1);> >this>.C =>new> Array(2 * t);> >this>.n = 0;> >}> >// A function to traverse all nodes in a subtree rooted with this node> >traverse()> >{> >// There are n keys and n+1 children, traverse through n keys> >// and first n children> >let i = 0;> >for> (i = 0; i <>this>.n; i++) {> > >// If this is not leaf, then before printing key[i],> >// traverse the subtree rooted with child C[i].> >if> (>this>.leaf ==>false>) {> >C[i].traverse();> >}> >document.write(keys[i] +>' '>);> >}> > >// Print the subtree rooted with last child> >if> (leaf ==>false>)> >C[i].traverse();> >}> > >// A function to search a key in the subtree rooted with this node.> >search(k)>// returns NULL if k is not present.> >{> > >// Find the first key greater than or equal to k> >let i = 0;> >while> (i keys[i])> >i++;> > >// If the found key is equal to k, return this node> >if> (keys[i] == k)> >return> this>;> > >// If the key is not found here and this is a leaf node> >if> (leaf ==>true>)> >return> null>;> > >// Go to the appropriate child> >return> C[i].search(k);> >}> }> // This code is contributed by patel2127> |
>
>
Piezīme: Iepriekš minētais kods nesatur draivera programmu. Mēs apskatīsim visu programmu mūsu nākamajā ierakstā B-koka ievietošana .
Ir divas konvencijas, lai definētu B-koku, viens ir definēt pēc minimālās pakāpes, otrs ir definēt pēc kārtas. Mēs esam ievērojuši minimālo grādu konvenciju un ievērosim to arī nākamajos ierakstos vietnē B-Tree. Iepriekš minētajā programmā izmantotie mainīgo nosaukumi arī paliek nemainīgi
B-Trees pielietojumi:
- To izmanto lielās datu bāzēs, lai piekļūtu diskā saglabātajiem datiem
- Izmantojot B-Tree, datu meklēšanu datu kopā var veikt ievērojami īsākā laikā
- Izmantojot indeksēšanas funkciju, var panākt daudzlīmeņu indeksēšanu.
- Lielākā daļa serveru izmanto arī B-koka pieeju.
- B-koki tiek izmantoti CAD sistēmās, lai organizētu un meklētu ģeometriskos datus.
- B-koki tiek izmantoti arī citās jomās, piemēram, dabiskās valodas apstrādē, datortīklos un kriptogrāfijā.
B-koku priekšrocības:
- B-Trees ir garantēta laika sarežģītība O(log n) pamata darbībām, piemēram, ievietošanai, dzēšanai un meklēšanai, kas padara tos piemērotus lielām datu kopām un reāllaika lietojumprogrammām.
- B-koki paši līdzsvaro.
- Augsta vienlaicīgums un liela caurlaidspēja.
- Efektīva uzglabāšanas izmantošana.
B-koku trūkumi:
- B-Trees pamatā ir diska datu struktūras, un tiem var būt liels diska lietojums.
- Nav labākais visiem gadījumiem.
- Lēns salīdzinājumā ar citām datu struktūrām.
Ievietošana un dzēšana:
B-koka ievietošana
B koku dzēšana