Ņemot vērā a BST , uzdevums ir meklēt mezglu šajā BST .
Lai meklētu vērtību BST, uzskatiet to par sakārtotu masīvu. Tagad mēs varam viegli veikt meklēšanas darbību BST, izmantojot Binārās meklēšanas algoritms .
Algoritms atslēgas meklēšanai noteiktā binārajā meklēšanas kokā:
Pieņemsim, ka vēlamies meklēt numuru X, Mēs sākam no saknes. Pēc tam:
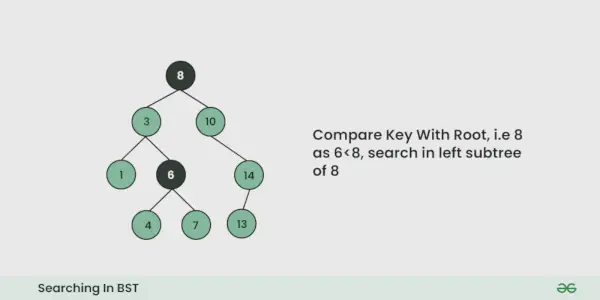
- Mēs salīdzinām meklējamo vērtību ar saknes vērtību.
- Ja tas ir vienāds, mēs pabeidzam meklēšanu, ja tas ir mazāks, mēs zinām, ka mums ir jāiet uz kreiso apakškoku, jo binārā meklēšanas kokā visi kreisā apakškoka elementi ir mazāki un visi labā apakškoka elementi ir lielāki.
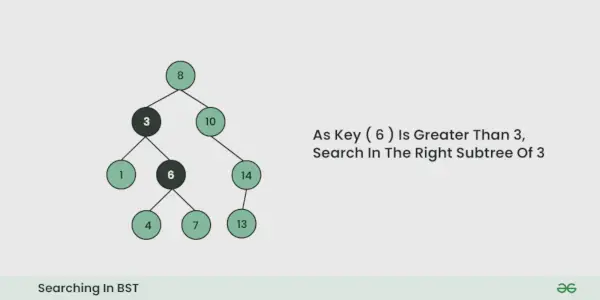
- Atkārtojiet iepriekš minēto darbību, līdz vairs nav iespējams pārvietoties
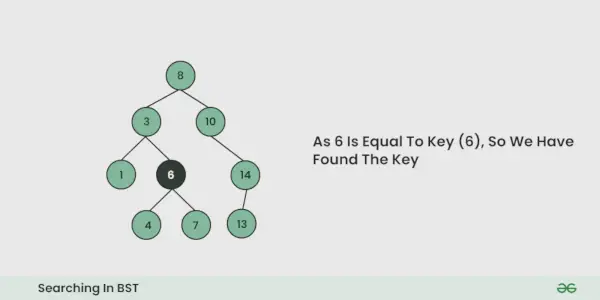
- Ja kādā iterācijā atslēga tiek atrasta, atgrieziet True. Citādi Nepatiesi.
Ilustrācija par meklēšanu BST:
Lai labāk izprastu, skatiet tālāk redzamo ilustrāciju:
Ieteicamā prakseMeklējiet mezglu BSTTIzmēģiniet to!
javascript izsaukšanas funkcija no html
Programma meklēšanas ieviešanai BST:
C++
// C++ function to search a given key in a given BST> #include> using> namespace> std;> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >=>new> struct> node;> >temp->atslēga = prece;> >temp->pa kreisi = temp->right = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);> >else> if> (key>mezgls->atslēga)> >node->pa labi = ievietot(mezgls->labais, atslēga);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > >// Base Cases: root is null or key is present at root> >if> (root == NULL> // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >cout << key <<>' not found'> << endl;> >else> >cout << key <<>' found'> << endl;> >return> 0;> }> |
>
>
C
// C function to search a given key in a given BST> #include> #include> struct> node {> >int> key;> >struct> node *left, *right;> };> // A utility function to create a new BST node> struct> node* newNode(>int> item)> {> >struct> node* temp> >= (>struct> node*)>malloc>(>sizeof>(>struct> node));> >temp->atslēga = prece;> >temp->pa kreisi = temp->right = NULL;> >return> temp;> }> // A utility function to insert> // a new node with given key in BST> struct> node* insert(>struct> node* node,>int> key)> {> >// If the tree is empty, return a new node> >if> (node == NULL)> >return> newNode(key);> >// Otherwise, recur down the tree> >if> (key key)> >node->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);> >else> if> (key>mezgls->atslēga)> >node->pa labi = ievietot(mezgls->labais, atslēga);> >// Return the (unchanged) node pointer> >return> node;> }> // Utility function to search a key in a BST> struct> node* search(>struct> node* root,>int> key)> > // Driver Code> int> main()> {> >struct> node* root = NULL;> >root = insert(root, 50);> >insert(root, 30);> >insert(root, 20);> >insert(root, 40);> >insert(root, 70);> >insert(root, 60);> >insert(root, 80);> >// Key to be found> >int> key = 6;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >key = 60;> >// Searching in a BST> >if> (search(root, key) == NULL)> >printf>(>'%d not found
'>, key);> >else> >printf>(>'%d found
'>, key);> >return> 0;> }> |
>
>
Java
// Java program to search a given key in a given BST> class> Node {> >int> key;> >Node left, right;> >public> Node(>int> item) {> >key = item;> >left = right =>null>;> >}> }> class> BinarySearchTree {> >Node root;> >// Constructor> >BinarySearchTree() {> >root =>null>;> >}> >// A utility function to insert> >// a new node with given key in BST> >Node insert(Node node,>int> key) {> >// If the tree is empty, return a new node> >if> (node ==>null>) {> >node =>new> Node(key);> >return> node;> >}> >// Otherwise, recur down the tree> >if> (key node.left = insert(node.left, key); else if (key>mezgls.atslēga) node.right = insert(mezgls.labais, atslēga); // Atgriezt (nemainītā) mezgla rādītāja atgriešanas mezglu; } // Lietderības funkcija atslēgas meklēšanai BST mezglā (mezgla sakne, int atslēga) // Draivera kods public static void main(String[] args) { BinarySearchTree tree = new BinarySearchTree(); // Mezglu ievietošana tree.root = koks.insert(koks.sakne, 50); koks.ievietot(koks.sakne, 30); koks.ievietot(koks.sakne, 20); koks.ievietot(koks.sakne, 40); koks.ievietot(koks.sakne, 70); koks.ievietot(koks.sakne, 60); koks.ievietot(koks.sakne, 80); // Atslēga jāatrod int atslēga = 6; // Meklē BST if (tree.search(tree.root, key) == null) System.out.println(key + ' not found'); else System.out.println(atslēga + ' atrasta'); atslēga = 60; // Meklē BST if (tree.search(tree.root, key) == null) System.out.println(key + ' not found'); else System.out.println(atslēga + ' atrasta'); } }> |
>
>
Python3
skudra pret maven
# Python3 function to search a given key in a given BST> class> Node:> ># Constructor to create a new node> >def> __init__(>self>, key):> >self>.key>=> key> >self>.left>=> None> >self>.right>=> None> # A utility function to insert> # a new node with the given key in BST> def> insert(node, key):> ># If the tree is empty, return a new node> >if> node>is> None>:> >return> Node(key)> ># Otherwise, recur down the tree> >if> key node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Atgriezt (nemainītu) mezgla rādītāja atgriešanas mezglu # Utilīta funkcija, lai meklētu atslēgu BST def meklēšanā (sakne, atslēga): # Pamata gadījumi: sakne ir Nulle vai atslēga atrodas saknē, ja sakne ir None vai root.key == atslēga: return root # Key ir lielāka par root's key if root.key return search(root.right, key) # Atslēga ir mazāka par sakni 's key return search(root.left, key) # Draivera kods if __name__ == '__main__': root = Nav root = ievietot(sakne, 50) insert(root, 30) insert(root, 20) insert (sakne, 40) ievietot(sakne, 70) ievietot(sakne, 60) ievietot(sakne, 80) # Atrodams taustiņš = 6 # Meklēšana BST, ja meklēšana(sakne, atslēga) ir None: print(key, 'nav atrasts') else: print(atslēga, 'atrasts') taustiņš = 60 # Meklēšana BST, ja meklēšana (sakne, atslēga) ir None: print(atslēga, 'nav atrasts') else: print(atslēga, 'atrasts')> |
>
>
C#
// C# function to search a given key in a given BST> using> System;> public> class> Node {> >public> int> key;> >public> Node left, right;> }> public> class> BinaryTree {> >// A utility function to create a new BST node> >public> Node NewNode(>int> item)> >{> >Node temp =>new> Node();> >temp.key = item;> >temp.left = temp.right =>null>;> >return> temp;> >}> >// A utility function to insert> >// a new node with given key in BST> >public> Node Insert(Node node,>int> key)> >{> >// If the tree is empty, return a new node> >if> (node ==>null>)> >return> NewNode(key);> >// Otherwise, recur down the tree> >if> (key node.left = Insert(node.left, key); else if (key>node.key) node.right = Ievietot(mezgls.labais, atslēga); // Atgriezt (nemainītā) mezgla rādītāja atgriešanas mezglu; } // Lietderības funkcija atslēgas meklēšanai BST publiskā mezgla meklēšanā (mezgla sakne, int atslēga) // Pamata gadījumi: sakne ir null vai atslēga atrodas saknē if (root == null // Draivera kods public static void Galvenā () { Node root = null; BinaryTree (sakne) , 40; bt.Insert(root, 60); bt.Insert(root, 80); bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(atslēga + 'atslēga = 60); if (bt.Search(root, key) == null) Console.WriteLine(key + ' not found'); else Console.WriteLine(key + ' found' } }>'>); |
java šķirošanas masīvs
>
// Javascript function to search a given key in a given BST>class Node {>>constructor(key) {>>this>.key = key;>>this>.left =>null>;>>this>.right =>null>;>>}>}>// A utility function to insert>// a new node with given key in BST>function>insert(node, key) {>>// If the tree is empty, return a new node>>if>(node ===>null>) {>>return>new>Node(key);>>}>>// Otherwise, recur down the tree>>if>(key node.left = insert(node.left, key); } else if (key>mezgls.atslēga) { mezgls.labais = ievietot(mezgls.labais, atslēga); } // Atgriezt (nemainītā) mezgla rādītāja atgriešanas mezglu; } // Lietderības funkcija atslēgas meklēšanai BST funkcijā search(root, key) { // Pamata gadījumi: sakne ir null vai atslēga atrodas saknē if (root === null || root.key === taustiņš ) { atgriezt sakni; } // Atslēga ir lielāka par saknes atslēgu if (root.key return search(root.right, key); } // Atslēga ir mazāka par root's key return search(root.left, key); } // Driver Code let root = insert(root, 30 insert(root, 70); 60 atrasts');} else { console.log(key + ' found' } key = 60 // Meklēšana BST failā if (search(root, key) === null) { console.log(); taustiņš + ' nav atrasts');>6 not found 60 found> Laika sarežģītība: O(h), kur h ir BST augstums.
Palīgtelpa: O(h), kur h ir BST augstums. Tas ir tāpēc, ka maksimālais vietas daudzums, kas nepieciešams, lai saglabātu rekursijas steku, būtu h .Saistītās saites:
- Binārās meklēšanas koka ievietošanas darbība
- Binārās meklēšanas koka dzēšanas darbība