- Mēs esam pētījuši stratēģijas, kuras var spriest gan uz priekšu, gan atpakaļ, taču abu virzienu sajaukums ir piemērots sarežģītas un lielas problēmas risināšanai. Šāda jaukta stratēģija ļauj vispirms atrisināt problēmas lielāko daļu un pēc tam atgriezties un atrisināt mazās problēmas, kas rodas, apvienojot problēmas lielās daļas. Tādu tehniku sauc Līdzekļu un mērķu analīze .
- Līdzekļu un mērķu analīze ir problēmu risināšanas metodes, ko izmanto mākslīgajā intelektā, lai ierobežotu meklēšanu AI programmās.
- Tas ir atpakaļ un uz priekšu meklēšanas tehnikas sajaukums.
- MEA tehniku 1961. gadā pirmo reizi ieviesa Alens Ņūls un Herberts A. Saimons savā problēmu risināšanas datorprogrammā, kas tika nosaukta par vispārējo problēmu risinātāju (GPS).
- MEA analīzes process koncentrējās uz pašreizējā stāvokļa un mērķa stāvokļa atšķirības novērtēšanu.
Kā darbojas līdzekļu un mērķu analīze:
Līdzekļu un mērķu analīzes procesu var piemērot problēmai rekursīvi. Tā ir stratēģija, lai kontrolētu meklēšanu problēmu risināšanā. Tālāk ir norādīti galvenie soļi, kas apraksta MEA metodes darbību problēmas risināšanā.
Linux komandas
- Vispirms novērtējiet atšķirību starp sākotnējo stāvokli un galīgo stāvokli.
- Atlasiet dažādus operatorus, kurus var piemērot katrai atšķirībai.
- Pielietojiet operatoru katrai atšķirībai, kas samazina atšķirību starp pašreizējo stāvokli un mērķa stāvokli.
Operatora apakšmērķu noteikšana
MEA procesā mēs atklājam atšķirības starp pašreizējo stāvokli un mērķa stāvokli. Kad šīs atšķirības rodas, mēs varam izmantot operatoru, lai samazinātu atšķirības. Bet dažreiz ir iespējams, ka operatoru nevar piemērot pašreizējam stāvoklim. Tātad mēs izveidojam pašreizējā stāvokļa apakšproblēmu, kurā var pielietot operatoru, tiek saukts tāds atpakaļgaitas ķēdes veids, kurā tiek atlasīti operatori un pēc tam tiek uzstādīti apakšmērķi, lai izveidotu operatora priekšnoteikumus. Operatora apakšmērķu noteikšana .
Līdzekļu un mērķu analīzes algoritms:
Pieņemsim pašreizējo stāvokli kā PAŠREIZĒJĀ un mērķa stāvokli kā MĒRĶI, tad tālāk ir norādītas MEA algoritma darbības.
- Izvēlieties jaunu operatoru O, kas ir piemērojams pašreizējai starpībai, un, ja tāda nav, signāla kļūme.
- Mēģiniet lietot operatoru O CURRENT. Izveidojiet divu stāvokļu aprakstu.
i) O-Start, stāvoklis, kurā ir izpildīti O priekšnosacījumi.
ii) O-rezultāts — stāvoklis, kas rastos, ja O tiktu lietots O startē. - Ja
(Pirmā daļa<------ mea (current, o-start)< strong>
Un
(PĒDĒJĀ daļa<----- mea (o-result, goal)< strong>, ir veiksmīgi, pēc tam signalizē par panākumiem un atgriež FIRST-PART, O un LAST-PART apvienošanas rezultātu.
Iepriekš apskatītais algoritms ir vairāk piemērots vienkāršai problēmai un nav piemērots sarežģītu problēmu risināšanai.
Vidējo mērķu analīzes piemērs:
Ņemsim piemēru, kur mēs zinām sākotnējo stāvokli un mērķa stāvokli, kā norādīts tālāk. Šajā problēmā mums ir jāiegūst mērķa stāvoklis, atrodot atšķirības starp sākotnējo stāvokli un mērķa stāvokli un piemērojot operatorus.
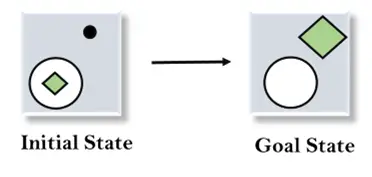
Risinājums:
Lai atrisinātu iepriekš minēto problēmu, mēs vispirms atradīsim atšķirības starp sākotnējiem stāvokļiem un mērķa stāvokļiem, un katrai atšķirībai mēs ģenerēsim jaunu stāvokli un izmantosim operatorus. Mūsu operatori šai problēmai ir:
1. Sākotnējā stāvokļa novērtēšana: Pirmajā darbībā mēs novērtēsim sākotnējo stāvokli un salīdzināsim sākotnējo un mērķa stāvokli, lai atrastu atšķirības starp abiem stāvokļiem.

2. Dzēst operatora lietošana: Kā mēs varam pārbaudīt, pirmā atšķirība ir tāda, ka mērķa stāvoklī nav punkta simbola, kas atrodas sākotnējā stāvoklī, tāpēc vispirms izmantosim Dzēst operatoru lai noņemtu šo punktu.

3. Move Operator lietošana: Pēc operatora Dzēst pielietošanas parādās jaunais stāvoklis, kuru mēs atkal salīdzināsim ar mērķa stāvokli. Pēc šo stāvokļu salīdzināšanas ir vēl viena atšķirība, proti, kvadrāts atrodas ārpus apļa, tāpēc mēs izmantosim Pārvietot operatoru .

4. Izvēršanas operatora lietošana: Tagad trešajā darbībā tiek ģenerēts jauns stāvoklis, un mēs salīdzināsim šo stāvokli ar mērķa stāvokli. Pēc štatu salīdzināšanas joprojām ir viena atšķirība, kas ir laukuma lielums, tāpēc mēs pielietosim Izvērst operatoru , un visbeidzot, tas ģenerēs mērķa stāvokli.

