Ievads
Vigenere šifrs ir algoritms, ko izmanto teksta šifrēšanai un atšifrēšanai. Vigenere šifrs ir alfabēta teksta šifrēšanas algoritms, kurā tiek izmantota virkne savstarpēji savienotu cēzara šifru. Tas ir balstīts uz atslēgvārda burtiem. Tas ir polialfabētiskā aizstāšanas šifra piemērs. Šo algoritmu ir viegli saprast un ieviest. Šo algoritmu pirmo reizi aprakstīja 1553. gadā Džovans Batista Belaso . Teksta šifrēšanai un atšifrēšanai tiek izmantota Vigenere tabula vai Vigenere kvadrāts. Vigenere tabulu sauc arī par tabula recta.
Vigenere šifrēšanu veic divas metodes.
1. metode
Kad ir dota vigenere tabula, šifrēšana un atšifrēšana tiek veikta, izmantojot vigenere tabulu (26 * 26 matrica) šajā metodē.
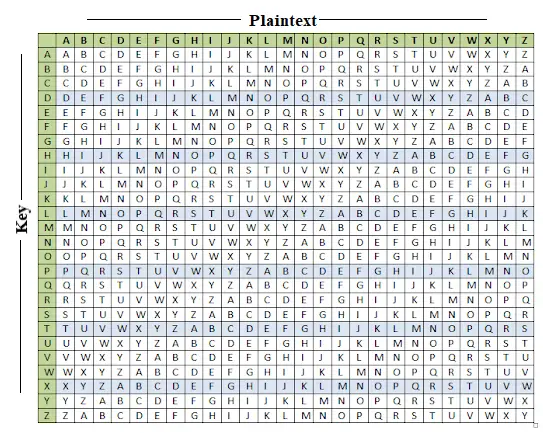
Piemērs: vienkāršais teksts ir 'JAVATPOINT', un atslēga ir 'BEST'.
Lai ģenerētu jaunu atslēgu, dotā atslēga tiek atkārtota apļveida veidā, ja vien vienkāršā teksta garums nav vienāds ar jauno atslēgu.

Šifrēšana
kad beidzas q1
Vienkāršā teksta pirmais burts tiek apvienots ar atslēgas pirmo burtu. Vienkāršā teksta kolonna “J” un atslēgas “B” rinda krustojas ar “K” alfabētu vigenere tabulā, tāpēc šifrētā teksta pirmais burts ir “K”.
Līdzīgi vienkāršā teksta otrais burts tiek apvienots ar atslēgas otro burtu. Vienkāršā teksta kolonna “A” un atslēgas “E” rinda krustojas ar “E” alfabētu vigenere tabulā, tāpēc šifrētā teksta otrais burts ir “E”.
Šis process turpinās nepārtraukti, līdz vienkāršais teksts ir pabeigts.
Šifrēts teksts = KENTUTGBOX
Atšifrēšana
Atšifrēšana tiek veikta, izmantojot atslēgu rindu vigenere tabulā. Vispirms atlasiet atslēgas burta rindu, atrodiet šifrētā teksta burta pozīciju šajā rindā un pēc tam atlasiet atbilstošā šifrētā teksta kolonnas apzīmējumu kā vienkāršu tekstu.

Piemēram, atslēgas rindā ir “B” un šifrētais teksts ir “K”, un šis šifrētā teksta burts parādās kolonnā “J”, tas nozīmē, ka pirmais vienkāršā teksta burts ir “J”.
Tālāk atslēgas rindā ir “E” un šifrētais teksts ir “E”, un šis šifrētā teksta burts parādās kolonnā “A”, tas nozīmē, ka otrais vienkāršā teksta burts ir “A”.
masīva virkne c
Šis process turpinās nepārtraukti, līdz šifrētais teksts ir pabeigts.
Vienkāršs teksts = JAVATPOINT
2. metode
Ja vigenere tabula nav norādīta, šifrēšana un atšifrēšana tiek veikta ar Vigenar algebrisko formulu šajā metodē (pārvērš burtus (A-Z) skaitļos (0-25)).
Šifrēšanas formula ir,
UNi= (Pi+ Ki) pret 26Atšifrēšanas formula ir,
Di= (Ei- Ki) pret 26Ja kāds gadījums (Di) vērtība kļūst negatīva (-ve), šajā gadījumā mēs pievienosim 26 negatīvajai vērtībai.
kur,
E apzīmē šifrēšanu.
Belforda algoritms
D apzīmē atšifrēšanu.
P apzīmē vienkāršu tekstu.
K apzīmē atslēgu.
Piezīme: “i” apzīmē burtu i-tā skaitļa nobīdi, kā parādīts tabulā zemāk.

Piemērs: vienkāršais teksts ir 'JAVATPOINT', un atslēga ir 'BEST'.
Šifrēšana: UNi= (Pi+ Ki) pret 26
java slēdzis int
| Vienkāršs teksts | Dž | A | IN | A | T | P | O | es | N | T |
| Vienkāršā teksta vērtība (P) | 09 | 00 | divdesmitviens | 00 | 19 | piecpadsmit | 14 | 08 | 13 | 19 |
| Atslēga | B | UN | S | T | B | UN | S | T | B | UN |
| Atslēgas vērtība (K) | 01 | 04 | 18 | 19 | 01 | 04 | 18 | 19 | 01 | 04 |
| Šifrēta teksta vērtība (E) | 10 | 04 | 13 | 19 | divdesmit | 19 | 06 | 01 | 14 | 23 |
| Šifrēts teksts | K | UN | N | T | IN | T | G | B | O | X |
Atšifrēšana: Di= (Ei- Ki) pret 26
Ja kāda gadījuma (Di) vērtība kļūst negatīva (-ve), šajā gadījumā mēs pievienosim 26 negatīvajai vērtībai. Tāpat kā šifrētā teksta trešais burts;
N = 13 un S = 18
Di= (Ei- Ki) pret 26
Di= (13 - 18) pret 26
Di= -5 pret 26
Di= (-5 + 26) pret 26
Di= 21
| Šifrēts teksts | K | UN | N | T | IN | T | G | B | O | X |
| Šifrēta teksta vērtība (E) | 10 | 04 | 13 | 19 | divdesmit | 19 | 06 | 01 | 14 | 23 |
| Atslēga | B | UN | S | T | B | UN | S | T | B | UN |
| Atslēgas vērtība (K) | 01 | 04 | 18 | 19 | 01 | 04 | 18 | 19 | 01 | 04 |
| Vienkāršā teksta vērtība (P) | 09 | 00 | divdesmitviens | 00 | 19 | piecpadsmit | 14 | 08 | 13 | 19 |
| Vienkāršs teksts | Dž | A | IN | A | T | P | O | es | N | T |
Programma:
C valoda
#include #include using namespace std; int main() { Vigenere cipher('VIGENERECIPHER'); string original = 'I AM INDIAN'; string encrypted = cipher.encrypt(original); string decrypted = cipher.decrypt(encrypted); cout << original << endl; cout << 'Encrypted: ' << encrypted << endl; cout << 'Decrypted: ' << decrypted << endl; } class Vigenere { public: string key; Vigenere(string key) { for (int i = 0; i = 'A' && key[i] key += key[i]; else if (key[i]>= 'a' && key[i] key += key[i] + 'A' - 'a'; } } string encrypt(string text) { string out; for (int i = 0, j = 0; i = 'a' && c <= 2 26 'z') c +="A" - 'a'; else if (c continue; out key[j] * 'a') % j="(j" 1) key.length(); } return out; string decrypt(string text) { for (int i="0," && <="z" ) 26) }; pre> <p> <strong>Output:</strong> </p> <pre> I AM INDIAN Encrypted: SDERFGTUJ Decrypted: IAMINDIAN </pre> <hr></=> 