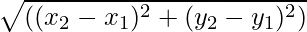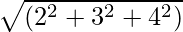logo

TechCodeview

Vektora lielums

Vektoru lielumi ir lielumi, kuriem ir gan virziens, gan lielums. Vektora lielums ir vektora garums. To nosaka vektora skaitliskā vērtība, un, tā kā tas attēlo vektora garumu, tas vienmēr ir pozitīvs. Jebkuram vektoram 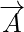overrightarrow{A}tā lielums ir attēlots kā overrightarrow{A}.

Šajā rakstā uzzināsim vairāk par vektora lielumu, tā formulu, piemēriem un citiem.



Satura rādītājs

Kāds ir vektora lielums?

Vektora lielums ir definēts kā vektora garums. Tā kā vektora lielums apzīmē vektora garumu, tas vienmēr ir pozitīvs. Jebkuram vektoram A tā lielums tiek attēlots kā |A|. Pieņemsim, ka vektors ir definēts kā xi + yj, tad tā lielums tiek definēts kā kvadrātsakne no atsevišķo terminu kvadrātu summas. Vektora lielums atspoguļo vektora garumu, t.i., vektora vērtību vai ietekmi.

Piemēram, ja uz objektu darbojas spēks 5i N, tad tā lielums ir 5 N, kas nozīmē, ka pielietotā spēka stiprums ir 5 N, un ' es' 5i nozīmē, ka tas tiek piemērots pozitīvā x virzienā.



Vektora formulas lielums

Ir dažādi veidi, kā aprēķināt vektora lielumu. Pamatojoties uz dotajiem datiem, izmantojiet cita veida formulu, lai atrastu vektora lielumu. Vektora A lielumu attēlo, izmantojot moduļa operatoru, t.i., |A|

Ir dažādas formulas, ko izmanto vektora lieluma saskaitīšanai. Nākamajā attēlā parādītas svarīgās formulas, kas izmantotas vektora lieluma noteikšanai.

Vektora formulas lielums

Tālāk ir sniegti veidi, kā aprēķināt lielumu.



  • Ja tiem ir dots vektors Ā = xi+ yĵ + zk̂, tad vektora Ā lielumu var aprēķināt, izmantojot zemāk esošo formulu

Vektora Ā lielums (|A|) = √(x 2 + un 2 +z 2 )

  • Ja sākuma punkta vektors ir (x1, un1) un vektora beigu punkts ir teikt (x2, un2) ir doti vektora lielums overrightarrow{AB}dod,
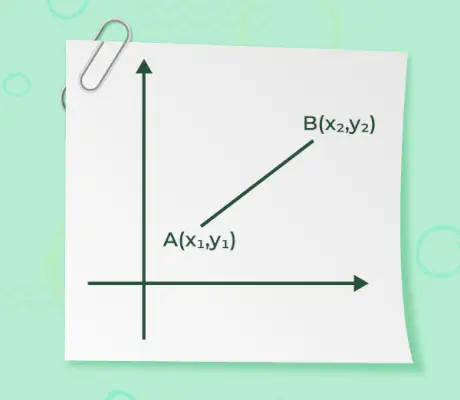
Vektora lielums, ja ir doti divi punkti

Vektora lielums, kad ir dots vektora sākuma un beigu punkts, nav nekas cits kā attālums starp punktiem. Lieluma atrašanas formula ir dota ar

overrightarrow{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Ja kāds no vektora sākuma vai beigu punktiem atrodas o(0, 0) un cits punkts ir A(x, y) kā norādīts zemāk esošajā attēlā,
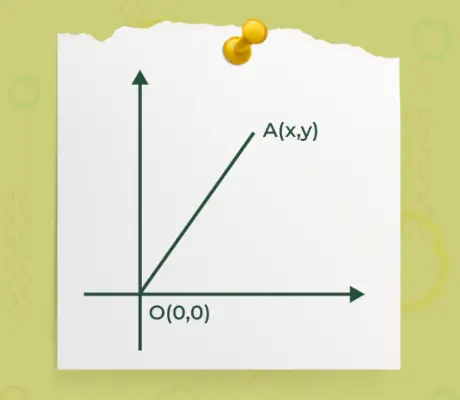
Vektora lielums, ja ir dots viens punkts un sākumpunkts

Tad formulu vektora lieluma noteikšanai, kur viens no vektora galiem atrodas sākuma punktā, dod

|Ā| = √(x 2 +y 2 )

Vektora virziens

Vektoru lielumi ir lielumi, kuriem ir gan lielumi, gan virzieni. Vektora daudzuma virziens norāda, kurā virzienā tiek piemērots vektora daudzums. To definē kā leņķi, ko vektors veido ar horizontālo līniju vai x asi. To attēlo simbols a .

Zemāk esošajā attēlā ir parādīta bultiņa, kas tiek izmantota, lai parādītu vektora virzienu.

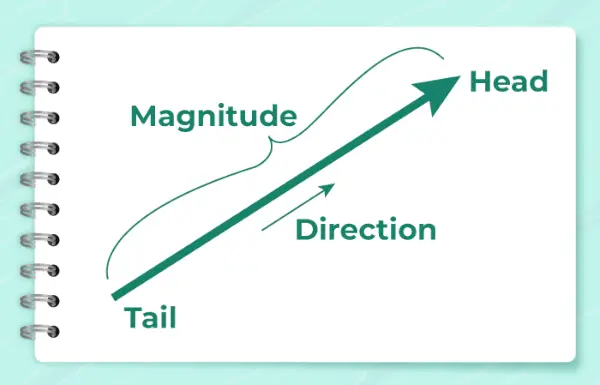
Vektora virziens

To aprēķina, izmantojot formulu,

α = iedegums -1 (y/x)

nulles pārbaude Java

Vektoram, ko ģenerē koordinātas (x1, un1) un (x2, un2) to virzienu nosaka formula,

α = iedegums -1 [(un 2 - un 1 )/(x 2 – x 1 )]

Kā atrast vektora lielumu?

Vektora lielumu aprēķina, izmantojot tālāk aprakstītās darbības,

1. darbība: Identificējiet vektora x, y un z komponentus.

2. darbība : atrodiet visu x, y un z komponentu kvadrātu.

3. darbība: Pievienojiet visus 2. darbībā atrastos kvadrātus.

4. darbība: Atrodiet kvadrātsakni no summas, kas iegūta 3. darbībā.

Pēc 4. soļa iegūtā vērtība ir dotā vektora lielums.

Piemērs: Atrodiet vektora A = 3i + 4j lielumu

Risinājums:

Vektora A lielumu aprēķina, izmantojot iepriekš aprakstītās darbības.

1. darbība: Salīdzinot A = 3i + 4j ar xi + yj, mēs iegūstam x = 3 un y = 4

2. darbība: x2= 32= 9 un y2= 42= 16

3. darbība: x2+ un2= 9 + 16 = 25

skati un galdi

4. darbība: √(25) = 5

Tādējādi vektora A = 3i + 4j lielums ir 5 vienības.

Secinājums

Noslēgumā jāsaka, ka vektora lielums norāda, cik garš ir vektors. Šī koncepcija ir ļoti svarīga daudzās jomās, piemēram, fizikā, inženierzinātnēs un datorzinātnēs, jo tā palīdz izmērīt tādas lietas kā ātrums, spēks un kustības virziens. Izprotot vektora lielumu, mēs varam labāk analizēt un atrisināt praktiskas problēmas, padarot to par galveno zināšanu daļu ikvienam, kas strādā ar skaitļiem un mērījumiem reālās pasaules lietojumprogrammās.

Lasīt vairāk,

Atrisināti piemēri par vektora lielumu

1. piemērs: Atrodiet vektora Ā = 2i + 3ĵ + 4k lielumu.

Risinājums:

virkne līdz veselam skaitlim java

Ņemot vērā,

Ā = 2i + 3ĵ + 4k

Lielums |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

Vektora lielums 2i+3ĵ+4k ir 5.38 vienība

2. piemērs: Atrodiet lielumu vektoram Ā = 3i + 3ĵ – 6k

Risinājums:

Ņemot vērā

Ā = 3i + 3ĵ – 6k

Lielums |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

Vektora lielums 3i+ 3ĵ – 6k ir 7.35 vienība.

3. piemērs. Atrodiet vektora lielumu, ja vektora sākuma punkts ir (3, 4) un beigu punkts ir (6, 2).

Risinājums:

Ņemot vērā,

(x1, un1) = (3, 4)
(x2, un2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

Tādējādi dotā vektora lielums ir 3.6 vienība.

pirmais klēpjdators

4. piemērs. Atrodiet vektora lielumu, ja vektora sākuma punkts ir (2, 1, 4) un beigu punkts ir (5, 2, 6).

Risinājums:

Ņemot vērā,

(x1, un1, Ar1) = (2, 1, 4)

(x2, un2, Ar2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Tādējādi dotā vektora lielums ir 3.74 vienība.

5. piemērs. Kāds ir vektora lielums, kas sākas no sākuma un beigu punktā (3, 4).

Risinājums:

Ņemot vērā,

Vektora sākuma punkts ir O(0, 0)

Beigu punkts (x, y) = (3, 4)

Vektora lielums (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Tādējādi dotā vektora lielums ir 5 vienība.

6. piemērs. Atrodiet vektora lielumu, kurā viens no gala punktiem atrodas sākuma punktā un otrs punkts (1, 4, 3).

Risinājums:

Ņemot vērā,

Vektora beigu punkts ir O(0, 0)

Cits punkts (x, y, z) = (1, 4, 3)

Vektora lielums (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Tādējādi dotā vektora lielums ir 5.09 vienība.

diāna ankudinova

Bieži uzdotie jautājumi par vektora lielumu

Kāds ir vektora formulas lielums?

Vektora lielums ir vektora skaitliskā vērtība, un tas nosaka vektora garumu. Jebkuram vektoram A tā lielums tiek attēlots kā |A|. Vektora lielumu aprēķina, izmantojot formulu,

Jebkuram vektoram A = xi + yj + zk tā lielumu nosaka formula

|A| = √(x 2 + un 2 + z 2 )

Jebkuram vektoram, kura sākuma punkts un beigu punkts ir attiecīgi (x1, un1) un (x2, un2) tā lielumu nosaka formula

|A| = √((x 2 – x 1 ) 2 + (un 2 - un 1 ) 2 )

Kā attēlot vektora lielumu?

Vektora lielums A ir apzīmēts ar simbolu |A|.

Kā atrast vektora lielumu?

Lai aprēķinātu vektora lielumu, tiek izmantotas dažādas formulas, dažas no tām ir,

  • |A| = √(x 2 + un 2 + z 2 ) kad vektors ir formā A = xi + yj + zk
  • |A| = √((x) 2 + (un) 2 ) kad vektors ir dots ar punktu A (x, y) un izcelsmi O(0, 0).
  • |A| = √((x 2 – x 1 ) 2 + (un 2 - un 1 ) 2 ) kad vektors ir dots ar punktu A (x1, un2) un punktu B (x2, un2).

Atrodiet 5 lieluma vektoru.

Ir dažādi vektori, kuru lielums var būt 5, piemēram, vektors A ir attēlots kā,

A = 3i + 4j vai A = 4i + 5j