Līdzīgi termini ir termini algebriskajās izteiksmēs, kuriem ir vienādi mainīgie, kas paaugstināti līdz vienādām pakāpēm. Vārdi Patīk un Atšķirīgi ir algebras terminu veidi, un mēs varam atšķirt līdzīgus un atšķirīgus terminus, vienkārši pārbaudot mainīgos un to pilnvaras. Mēs definējam algebriskos terminus kā atsevišķus terminus, kas iegūti no algebriskā vienādojuma.
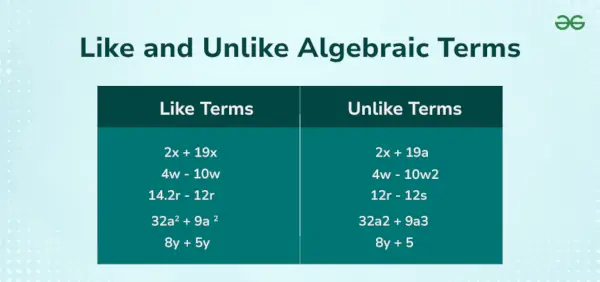
Piemēram, algebriskajā vienādojumā 5x + 3g 2 = 12 mums ir trīs termini, 5x, 3y², un 12 . Šeit, 5x, un 3 g 2 ir mainīgi termini, un 12 ir nemainīgs vārds. Zemāk esošajā attēlā ir parādīti līdzīgi un atšķirīgi termini.
Šajā rakstā mēs detalizēti uzzināsim par Patīk terminiem, Atšķirībā no terminiem, to piemēriem, vienkāršošanu un citiem.
Tāpat kā Noteikumi
Līdzīgi termini ir termini, kuriem ir vienādi mainīgie, un arī katra mainīgā jauda ir vienāda. Mēs varam apvienot līdzīgus terminus, lai vienkāršotu algebriskās izteiksmes, un to var ļoti viegli aprēķināt. Piemēram, 3y + 5y ir algebriska izteiksme ar līdzīgiem terminiem 3y un 5y. Lai vienkāršotu šo algebrisko izteiksmi, mēs pievienojam līdzīgus terminus. Tādējādi dotās izteiksmes vienkāršojums ir 8y.
Līdzīgu terminu piemēri
Līdzīgi termini ir termini, kuriem ir viens un tas pats mainīgais ar līdzīgu jaudu. Daži līdzīgu terminu piemēri ir:
- 40xy 2 un 56xy 2 : Pirmajā piemērā xy2ir abu terminu kopējais koeficients. Tātad tie ir kā termini.
- 30z 2 un 18z 2 : Ar2ir abu terminu kopējais koeficients. Tātad tie ir kā termini.
- 45abc un 29abc: abc ir abu terminu kopējais koeficients. Tātad tie ir kā termini.
- 18r 3 un 38r 3 : r3ir abu terminu kopējais koeficients. Tātad tie ir kā termini.
- 2xy un 8xy: xy ir abu terminu kopējais koeficients. Tātad tie ir kā termini.
Līdzīgu terminu saskaitīšana un atņemšana
Mēs varam viegli veikt līdzīgu terminu saskaitīšanu un atņemšanu, un tam nav nepieciešami īpaši noteikumi, tie parasti tiek vienkāršoti, izmantojot parastos saskaitīšanas un atņemšanas noteikumus. Mēs varam saprast šo jēdzienu, izmantojot šādu piemēru.
Piemērs: vienkāršojiet 11x 3 + 5x 3
c++ virknes sadalījums
Risinājums:
Kā redzam, tie ir kā termini, jo tiem ir līdzīgi mainīgie un arī to jauda ir nemainīga.
Mēs varam viegli pievienot šos terminus tieši.
= 11x3+ 5x3
= 16x3
Tas ir iespējams, jo tiem ir vienādi mainīgie ar līdzīgu jaudu, un to var saprast tā, ka mēs varam tieši pievienot rūpijas rūpijām, t.i., 5 Rs + 7 Rs ir 12 Rs. Bet mēs nevaram tieši pievienot rūpijas ar dolāriem, un 5 Rs + 7 dolārus nevar tieši vienkāršot.
Līdzīgi mēs varam arī tieši atņemt līdzīgus terminus, vienkārši pievienot mēs pievienojam līdzīgus terminus, ko var saprast ar šādu piemēru.
1. piemērs: vienkāršojiet 11 reizes 3 - 5x 3
Risinājums:
Kā redzam, tie ir kā termini, jo tiem ir līdzīgi mainīgie un arī to jauda ir nemainīga.
Mēs varam viegli atņemt šos terminus tieši.
= 11x3- 5x3
= 6x3
2. piemērs: pievienojiet 3 x + 2 un + 5 un 4 x – 3 un +7.
Risinājums:
(3 x + 2 un + 5) + (4 x – 3 un + 7)
= (3 x + 4 x) + (2 g + (-3 g))+ (5 + 7)
pārslēgt paziņojumu java= 7 x − un + 12
Atšķirībā no noteikumiem
Atšķirībā no terminiem ir termini ar dažādiem mainīgajiem, un katram mainīgajam var būt vai var nebūt dažādi eksponenti. Piemēram, 9x + 6y ir algebriska izteiksme ar atšķirībām no terminiem. Jo tam ir divi dažādi mainīgie x un y.
Ja mainīgie ir atšķirīgi, mēs nepārbaudām jaudu, jo tie nekādā veidā atšķiras no terminiem, bet, ja mainīgie ir vienādi, mēs pārbaudām to pilnvaras, jo tie var būt vai nebūt līdzīgi terminiem.
Piemēram, 5x2un 6x2ir kā termini, bet, 5x2un 6x3ir atšķirīgi termini.
Atšķirīgo noteikumu piemēri
Atšķirībā no terminiem ir termini, kuriem nav ne vienādu mainīgo, ne līdzīgas jaudas. Daži atšķirīgi terminu piemēri ir:
- 40xy 2 un 56xy: Šeit vienā algebriskajā izteiksmē mainīgais ir xy2un citā algebriskajā izteiksmē mainīgais ir xy. Abi mainīgie ir vienādi, bet tiem ir dažādas pilnvaras. Tātad tie atšķiras no terminiem.
- 45abc un 29ab: Šeit vienā algebriskajā izteiksmē mainīgais ir abc, bet otrā algebriskajā izteiksmē mainīgais ir ab. Abi mainīgie ir atšķirīgi. Tātad atšķirībā no terminiem tie ietilpst kategorijā.
Atšķirīgo terminu saskaitīšana un atņemšana
Saskaitīšana un atņemšana netiek veikta starp, atšķirībā no terminiem, t.i., mēs nevaram pievienot vai atņemt atšķirībā no vārdiem, un to var saprast ar piemēru, jo mēs nevaram pievienot 5 litrus piena ar 6 kg rīsu. Tādā pašā veidā mēs nevaram pievienot vai atņemt, atšķirībā no terminiem.
Piemēram, 3xy + 5x nevar tālāk atrisināt, un tas tiek atstāts tāpat.
Atšķirība starp līdzīgiem noteikumiem un atšķirībām no noteikumiem
Atšķirības starp līdzīgiem un atšķirīgiem terminiem ir aplūkotas tabulā zemāk.
| Funkcija | Tāpat kā Noteikumi | Atšķirībā no noteikumiem |
|---|---|---|
| Definīcija | Līdzīgi termini ir termini, kuriem ir vienādi mainīgie un tās pašas eksponenta vērtības. | Atšķirībā no terminiem ir termini, kuriem ir dažādi mainīgie un eksponenti. |
| Vienkāršošana | Mēs varam viegli vienkāršot līdzīgus terminus. | Atšķirībā no terminiem, kurus nevar vienkāršot. |
| Apvienojot terminus 100kmh līdz mph | Līdzīgus terminus var tieši apvienot, lai veiktu aprēķinus. | Atšķirībā no terminiem nevar kombinēt tieši, jo tie atspoguļo dažādus lielumus |
| Saskaitīšana vai atņemšana | Saskaitīšanu un atņemšanu var panākt līdzīgiem terminiem. | Atšķirībā no terminiem mēs nevaram pievienot vai atņemt. |
| Piemēri | Līdzīgu terminu piemēri ir x2, 5x2, -11/3x2utt. | Atšķirībā no terminu piemēri ir x2un 5x3, -11/3x utt. |
Lasīt vairāk
- Algebriskās izteiksmes
- Algebrisko izteiksmju veidi
Piemēri līdzīgiem un atšķirīgiem algebriskajiem terminiem
1. piemērs: norādiet vārdus “Patīk” un “Nepatīk” no: 3x, 5xy, 18x 2 un 5x 3 , 29xy, 50x 3
Risinājums:
Patīk un Atšķirībā no dotajiem terminiem ir,
Patīk noteikumi: (5xy, 29xy) un (5x3, 50x3)
Atšķirībā no noteikumiem: 3x, 18x2un
2. piemērs: vienkāršojiet 3xy + 5x 2 + 11ab – 4xy
modificēt failu linux
Risinājums:
Dotā izteiksme: 3xy + 5x2+ 11ab – 4xy
Tāpat kā termins dotajā izteiksmē, 3xy un -4xy
Vienkāršojot,
= 3xy – 4xy + 5x2+ 11ab
= -xy + 5x2+ 11ab
Visi noteikumi atšķiras no noteikumiem, tāpēc tos nevar tālāk atrisināt.
3. piemērs: vienkāršojiet 8x + 15x 2 + 11x – 4x 2
Risinājums:
Dotā izteiksme: 8x + 15x2+ 11x – 4x2
Līdzīgs termins dotajā izteiksmē, (8x, 11x) un (15x2, -4x2)
Vienkāršojot,
= 8x + 11x + 15x2- 4x2
= 19x – 11x2
Visi noteikumi atšķiras no noteikumiem, tāpēc tos nevar tālāk atrisināt.
Patīk un atšķirībā no algebriskiem terminiem — FAQ
Kas ir algebriskie termini?
Algebriskie termini ir atsevišķi termini, kas iegūti no algebriskā vienādojuma, t.i., termini, kas dalīti ar darbības simboliem, piemēram, + un -.
Kas ir līdzīgi un atšķirīgie termini?
Līdzīgi un atšķirīgie termini ir algebriskās izteiksmes termini. Līdzīgi mums ir līdzīgi mainīgie, un eksponenta jauda ir vienāda, savukārt atšķirībā no mainīgajiem un to jauda ir atšķirīga.
Kāda ir atšķirība starp līdzīgiem un atšķirībām algebriskajiem terminiem?
Galvenā atšķirība starp līdzīgiem un atšķirīgiem terminiem ir tāda, ka līdzīgā terminā mums ir viens un tas pats mainīgais ar vienādām pilnvarām, savukārt atšķirībā no terminiem mums ir dažādi mainīgie ar dažādām pakāpēm.
gulēt javascript
Kā atrast līdzīgus un atšķirīgus algebriskos terminus?
Līdzīgi termini ir termini, kuriem ir vienādi mainīgie ar vienādām pilnvarām, un atšķirīgie termini ir termini ar dažādiem mainīgajiem un dažādām pakāpēm, un mēs tos varam viegli identificēt, vienkārši pārbaudot mainīgos.
Vai mēs varam pievienot vai atņemt tāpat kā algebriskos terminus?
Mēs varam viegli pievienot vai atņemt līdzīgus vārdus, piemēram, 5x un 11x, ir līdzīgi termini, un tos var pievienot kā 16x.
Vai mēs varam pievienot vai atņemt atšķirībā no algebriskajiem terminiem?
Mēs nevaram pievienot vai atņemt atšķirībā no tādiem terminiem kā 2x un 3y. Tādējādi atšķirībā no terminiem nevar pievienot vai atņemt kopā.
