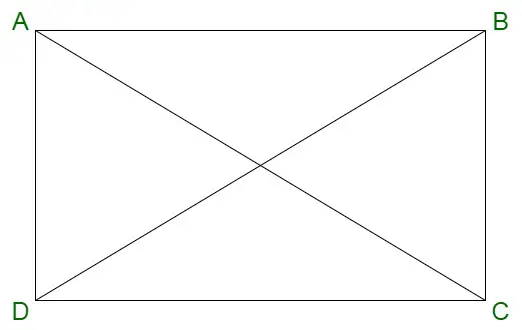
Vai katrs taisnstūris ir rombs? Taisnstūris ir divdimensiju ģeometriska figūra, kas attēlota ar četrām malām un četriem stūriem. Taisnstūrī ir tādas malas, ka pretējo malu garums ir vienāds un šīs malas ir paralēlas viena otrai. Sānu malām ir viens stūris no blakus esošajām malām ar 90° leņķi starp tām. Tāpēc taisnstūrī ir četri taisnstūra leņķi.

Satura rādītājs
- Taisnstūris
- Rombs
- Vai katrs taisnstūris ir rombs?
- Jautājumu paraugi – vai katrs taisnstūris ir rombs
Taisnstūris
Taisnstūra īpašības ir norādītas zemāk:
- Tam ir četras malas un četri stūri, kas pazīstami kā virsotnes.
- Taisnstūra diagonāles sadala viena otru uz pusēm.
- Taisnstūra laukums ir līdzvērtīgs tā garuma un platuma reizinājumam.
- Katrai virsotnei ir leņķis, kas vienāds ar 90O
- Taisnstūra pretējās malas ir vienādas un paralēlas viena otrai.
- Perimetrs ir vienāds ar divkāršu tā garuma un platuma summu.
- Visu iekšējo leņķu summa ir vienāda ar 360 grādiem
Taisnstūra perimetrs
Kopējo nobīdi, kas aptverta, izejot cauri taisnstūra robežai, var saukt par perimetru. Tā kā gan garumu, gan platumu apzīmē ar garuma vienību, perimetru mēra arī garuma vienībā.
Perimetru var apzīmēt ar,
Perimetrs, P = 2 (garums + platums)
Taisnstūra laukums
Apgabalu, ko plaknē aptver divdimensiju ģeometriskā figūra, sauc par figūras laukumu. Tādējādi taisnstūra laukums ir tā robežās ietvertais laukums. To mēra kvadrātveida vienībās. Laukums ir līdzvērtīgs taisnstūra garuma un platuma reizinājumam.
Apgabalu var apzīmēt ar,
Platība, A = garums × platums kvadrātvienības
Taisnstūra formulas diagonāle
Jebkuras ģeometriskas figūras diagonāles savieno alternatīvas virsotnes. Taisnstūra diagonāļu garumu var aprēķināt pēc šādas formulas, ko apzīmē ar d,
d = sqrt{( l^2 + w^2)} kur,
l = taisnstūra garums
w = taisnstūra platums
Lasīt detalizēti: Taisnstūra īpašības: definīcija, formulas, piemēri
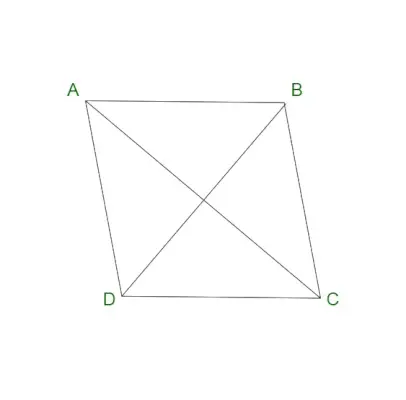
Rombs
Rombu sauc arī par četrpusīgu četrstūri. To uzskata par paralelograma īpašu gadījumu. Rombs satur paralēlas pretējās malas un vienādus pretējos leņķus. Rombs ir pazīstams arī ar nosaukumu dimants vai rombs dimants. Rombā visas romba malas ir vienādas garumā. Arī romba diagonāles sadala viena otru taisnā leņķī.
Romba īpašības
Rombam ir šādas īpašības:
- Rombs satur visas vienādas malas.
- Romba diagonāles sadala viena otru taisnā leņķī.
- Romba pretējās malas pēc būtības ir paralēlas.
- Divu blakus esošo romba leņķu summa ir vienāda ar 180O.
- Rombā nav uzraksta apļa.
- Ap rombu nav norobežojoša apļa.
- Romba diagonāles noved pie četru taisnleņķa trīsstūru veidošanās.
- Šie trīsstūri ir saskaņoti viens ar otru.
- Romba pretējie leņķi ir vienādi.
- Savienojot romba malu viduspunktu, veidojas taisnstūris.
- Kad pusi diagonāles viduspunkti ir savienoti, veidojas vēl viens rombs.
Romba perimetrs
Romba perimetrs ir definēts kā tā robežu kopējais garums, kas veido figūru. To var arī apzīmēt kā romba četru malu garuma kopējo summēšanu. Romba perimetru nosaka:
Perimetrs, P = 4a vienības
kur romba diagonāles apzīmē ar d1& d2un “a” ir puse.
Romba apgabals
Romba laukums ir definēts kā apgabals, kas ietverts divdimensiju plaknē. Romba laukums ir ekvivalents romba diagonāļu reizinājumam, kas dalīts ar 2. Romba laukumu var definēt ar šādu formulu:
Platība, A =
frac{(d_1 imes d_2)}{2} kv vienībaskur d1un d2ir romba diagonāles.
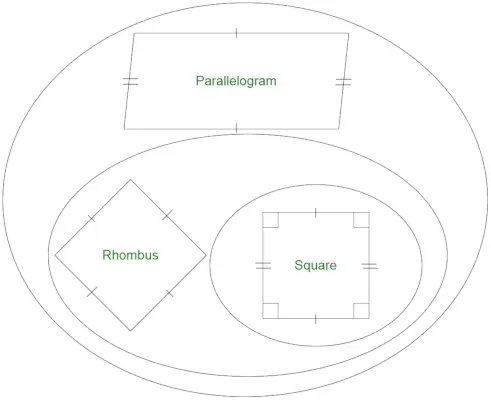
Mēs varam viegli pamanīt, ka katrs rombs ir paralelograms, bet otrādi nav taisnība. Kvadrātu var uzskatīt par īpašu romba gadījumu, jo tajā ir četras vienāda garuma malas. Kvadrātam ir visi taisnie leņķi. Tomēr visi romba leņķi ne vienmēr ir taisni . Visbeidzot, rombu, kas satur taisnus leņķus, var uzskatīt par kvadrātu. Tāpēc mēs varam teikt, ka
- Visi rombi ir paralelogrami.
- Visi paralelogrami nav rombi.
- Visi rombi nav kvadrāti.
- Visi kvadrāti ir rombi.
Vai katrs taisnstūris ir rombs?
Taisnstūris ir ģeometriska figūra, kurai nav vienādas malas. Kvadrāts ir īpašs taisnstūra gadījums ar vienādām malām. Tā kā mēs zinām, ka rombam ir vienādas malas. Taisnstūru un rombu kopas krustojas tikai kvadrātu gadījumā. Tāpēc taisnstūris nav rombs.
atšķirība starp bināro koku un bināro meklēšanas koku

Kāpēc rombs ir taisnstūris?
Rombs ir īpašs taisnstūra gadījums. Tā kā mēs zinām, ka romba diagonāles krustojas vienādos leņķos, bet taisnstūra diagonāles ir vienādas garumā. Savienojot romba malu viduspunktus, veidojas taisnstūris.
Lasīt vairāk: Kāpēc rombs nav kvadrāts?
Jautājumu paraugi – vai katrs taisnstūris ir rombs
1. jautājums. Aprēķiniet taisnstūra rāmja laukumu, kura izmērs ir 6 collas garums un 3 collas plats.
Risinājums:
Tā kā mēs zinām,
Taisnstūra laukums = (garums × platums) kvadrāta vienības.
Aizvietojot vērtības, mēs iegūstam,
taisnstūra rāmja laukums = 6 × 3 = 18 kvadrātcollas
2. jautājums. Atrodiet taisnstūra diagonāles garumu, kura garums ir attiecīgi 12 cm un platums 8 cm.
Risinājums:
Mēs zinām,
Diagonālais garums,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
3. jautājums. Atrodiet romba laukumu ar diviem diagonāles garumiem d 1 un d 2 būt attiecīgi 6 cm un 12 cm.
Risinājums:
Mums ir,
Diagonāle d1= 6 cm
Diagonāle d2= 12 cm
Romba laukumu nosaka,
A =
frac{(d_1 imes d_2)}{2} kv vienībasA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Tāpēc romba laukums = 36 cm2.
4. jautājums. Atšķirība starp rombu un taisnstūri?
Risinājums:
| Īpašums | Rombs | Taisnstūris |
| Sānu malas | Vienādas puses. | Pretējās puses ir vienādas. |
| Diagonāles | Diagonāles sadala viena otru 90° leņķī. Diagonāles centrā veido taisnus leņķus. | Diagonāles sadala viena otru dažādos leņķos. Viens leņķis ir strups leņķis, bet otrs ir akūts leņķis. Diagonāles centrā veido dažādus leņķus – strupleņķi un akūto leņķi. |
| Leņķi | Pretējie leņķi ir vienādi. Blakus esošie leņķi tiek pievienoti līdz 180°. | Pretējie un blakus leņķi ir vienādi. Leņķis, ko veido taisnstūra blakus esošās malas, ir 90°. |
