A Min-Heap ir definēts kā veids Kaudzes datu struktūra ir bināra koka veids, ko datorzinātnēs parasti izmanto dažādiem mērķiem, tostarp datu kārtošanai, meklēšanai un kārtošanai.
Ievads Min-Heap — datu struktūras un algoritmu apmācības
izrakstīšanās ar git
Min-Heap mērķis un lietošanas gadījumi:
- Prioritātes rindas ieviešana: Viens no primārajiem kaudzes datu struktūras lietojumiem ir prioritāro rindu ieviešana.
- Dijkstras algoritms : Dijkstra algoritms ir īsākā ceļa algoritms, kas atrod īsāko ceļu starp diviem diagrammas mezgliem. Minimālo kaudzi var izmantot, lai sekotu līdzi neapmeklētajiem mezgliem ar mazāko attālumu no avota mezgla.
- Kārtošana: Minimālo kaudzi var izmantot kā kārtošanas algoritmu, lai efektīvi kārtotu elementu kolekciju augošā secībā.
- Vidējais atradums: Minimālo kaudzi var izmantot, lai efektīvi atrastu skaitļu straumes mediānu. Mēs varam izmantot vienu min kaudzi, lai saglabātu lielāko daļu skaitļu, un vienu maksimālo kaudzi, lai saglabātu mazāko pusi. Mediāna būs minimālās kaudzes sakne.
Min-Heap datu struktūra dažādās valodās:
1. Min-Heap valodā C++
Minimālo kaudzi var ieviest, izmantojot prioritāte_rinda konteiners no standarta veidņu bibliotēkas (STL). The prioritāte_rinda konteiners ir konteinera adaptera veids, kas nodrošina veidu, kā saglabāt elementus rindai līdzīgā datu struktūrā, kurā katram elementam ir ar to saistīta prioritāte.
Sintakse :
C++ priority_queue < int, vector , lielāks > minH;>> 2. Min-Heap Java
Java programmā minimālo kaudzi var ieviest, izmantojot PriorityQueue klase no java.util pakotne . PriorityQueue klase ir prioritāra rinda, kas nodrošina veidu, kā saglabāt elementus rindai līdzīgā datu struktūrā, kurā katram elementam ir ar to saistīta prioritāte.
Sintakse :
JavaMin-Heap Python Programmā Python minimālo kaudzi var ieviest, izmantojot kaudze q modulis, kas nodrošina kaudžu ieviešanas funkcijas. Konkrēti, kaudze q modulis nodrošina veidu, kā izveidot un manipulēt ar kaudzes datu struktūrām.
Sintakse:
PythonC# valodā minimālo kaudzi var ieviest, izmantojot PriorityQueue klasi no System.Collections.Generic namespace . PriorityQueue klase ir prioritāra rinda, kas nodrošina veidu, kā saglabāt elementus rindai līdzīgā datu struktūrā, kurā katram elementam ir ar to saistīta prioritāte. Sintakse:
C# var minHeap = new PriorityQueue ();>>
5. Min-heap JavaScript
Minimālā kaudze ir binārs koks, kurā katram mezglam ir vērtība, kas ir mazāka vai vienāda ar tā bērniem. JavaScript var ieviest minimālo kaudzi, izmantojot masīvu, kur pirmais elements apzīmē saknes mezglu un mezgla atvases indeksā. i atrodas pie indeksiem 2i+1 un 2i+2.
Sintakse:
JavaScript Atšķirība starp Min Heap un Max Heap:
Minimālā kaudze
Max Heap
1.
kā iegūt iPhone emocijzīmes operētājsistēmā Android
Min-Heap atslēgai, kas atrodas saknes mezglā, ir jābūt mazākai vai vienādai ar to atslēgām, kas atrodas visos tā atvasumos.
Max-Heap atslēgai, kas atrodas saknes mezglā, ir jābūt lielākai vai vienādai ar atslēgām, kas atrodas visos tā atslēgpunktos.
2.
Min-Heap minimālais atslēgas elements atrodas saknē.
Max-Heap maksimālais atslēgas elements atrodas saknē.
3.
Min-Heap izmanto augošu prioritāti.
Max-Heap izmanto dilstošo prioritāti.
4.
Min-Heap konstrukcijā mazākajam elementam ir prioritāte.
Max-Heap konstrukcijā lielākajam elementam ir prioritāte.
5.
Min-Heap mazākais elements ir pirmais, kas tiek izmests no kaudzes.
Max-Heap lielākais elements ir pirmais, kas tiek izmests no kaudzes.
Min-Heap datu struktūras iekšējā ieviešana:
A Minimālā kaudze parasti tiek attēlota kā masīvs .
atgriežot masīvu java
- Saknes elements būs plkst Arr[0] .
- Jebkuram itajam mezglam Arr[i] :
- Arr[(i -1) / 2] atgriež savu vecāku mezglu.
- Arr[(2 * i) + 1] atgriež kreiso atvasināto mezglu.
- Arr[(2 * i) + 2] atgriež labo atvasināto mezglu.
Min-Heap iekšējai ieviešanai ir jāveic 3 galvenie soļi:
- Ievietošana : lai ievietotu elementu minimālajā kaudzē, vispirms pievienojam elementu masīva beigām un pēc tam pielāgojam kaudzes rekvizītu, atkārtoti apmainot elementu ar tā vecākelementu, līdz tas atrodas pareizajā pozīcijā.
- Dzēšana : Lai noņemtu minimālo elementu no minimālās kaudzes, vispirms saknes mezglu apmainām ar pēdējo masīva elementu, noņemam pēdējo elementu un pēc tam pielāgojam kaudzes rekvizītu, atkārtoti apmainot elementu ar tā mazāko pakārtoto elementu, līdz tas atrodas pareiza pozīcija.
- Veidot kaudzi : kaudzes palielināšanas darbību var izmantot, lai izveidotu minimālo kaudzi no nešķirota masīva.
Darbības ar minimālo kaudzes datu struktūru un to ieviešana:
Šeit ir dažas izplatītas darbības, kuras var veikt kaudzes datu struktūrā,
1. Ievietošana Min-Heap datu struktūrā :
Elementus var ievietot kaudzē, izmantojot līdzīgu pieeju, kā iepriekš aprakstīts dzēšanai. Ideja ir:
- Ievietošanas darbība min kaudzē ietver šādas darbības:
- Pievienojiet jauno elementu kaudzes galā nākamajā pieejamajā pozīcijā koka pēdējā līmenī.
- Salīdziniet jauno elementu ar tā vecāku elementu. Ja vecāks ir lielāks par jauno elementu, nomainiet tos.
- Atkārtojiet 2. darbību, līdz vecākais elements ir mazāks vai vienāds ar jauno elementu vai līdz jaunais elements sasniedz koka sakni.
- Jaunais elements tagad atrodas pareizajā pozīcijā min kaudzē, un kaudzes rekvizīts ir izpildīts.
Ilustrācija:
Pieņemsim, ka kaudze ir minimālā kaudze, kā:
Ievietošana Min-Heap
Ievietošanas operācijas ieviešana Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & kaudze, int vērtība) { // Pievienot jauno elementu kaudzes beigām.push_back(value); // Iegūstiet pēdējā elementa indeksu int index = heap.size() - 1; // Salīdziniet jauno elementu ar tā vecāku un apmainiet, ja // nepieciešams, kamēr (indekss> 0 && kaudze[(indekss - 1) / 2]> kaudze[indekss]) { swap(heap[indekss], kaudze[(indekss - 1) / 2]); // Pārvietot koku uz augšu uz pašreizējā // elementa vecāku // indeksa = (indekss - 1) / 2; } } // Galvenā funkcija, lai pārbaudītu funkciju insert_min_heap int main() { vector kaudze; int vērtības[] = {10, 7, 11, 5, 4, 13}; int n = lielums(vērtības) / lielums(vērtības[0]); for (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && kaudze[(indekss - 1) / 2]> kaudze[indekss]) { mijmaiņas(kaudze, indekss, (indekss - 1) / 2); // Pārvietot koku uz augšu uz pašreizējā // elementa vecāku // indeksa = (indekss - 1) / 2; } } // Funkcija, lai apmainītu divus elementus masīvā public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } // Galvenā funkcija, lai pārbaudītu funkciju insertMinHeap public static void main(String[] args) { int[] kaudze = new int[6]; int[] vērtības = {10, 7, 11, 5, 4, 13}; int izmērs = 0; for (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 un kaudze[(indekss - 1) // 2]> kaudze[indekss]: kaudze[indekss], kaudze[(rādītājs - 1) // 2] = kaudze[(indekss - 1) // 2], kaudze[ index] # Pārvietot koku uz augšu uz pašreizējā elementa vecāku indeksu = (indekss - 1) // 2 kaudze = [] vērtības = [10, 7, 11, 5, 4, 13] vērtībām vērtībās: insert_min_heap( kaudze, vērtība) print(f'Ievietota {value} minimālajā kaudzē: {heap}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List kaudze, int vērtība) { // Pievienot jauno elementu kaudzes kaudzes beigām.Pievienot(vērtība); // Iegūstiet pēdējā elementa indeksu int index = heap.Count - 1; // Salīdziniet jauno elementu ar tā vecāku un apmainiet // ja nepieciešams, kamēr (indekss> 0 && kaudze[(indekss - 1) / 2]> kaudze[indekss]) { int temp = kaudze[indekss]; kaudze[indekss] = kaudze[(indekss - 1) / 2]; kaudze [(indekss - 1) / 2] = temp; // Pārvietot koku uz augšu uz pašreizējā // elementa vecāku // indeksa = (indekss - 1) / 2; } } // Galvenā funkcija InsertMinHeap funkcijas pārbaudei public static void Main() { Saraksts kaudze = jauns saraksts (); int[] vērtības = {10, 7, 11, 5, 4, 13}; foreach(int vērtība vērtībās) { InsertMinHeap(heap, value); Console.Write('Ievietots ' + vērtība + ' minimālajā kaudzē: '); foreach(int elements kaudzē) { Console.Write(element + ' '); } Console.WriteLine(); } } }> Javascript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && kaudze[vecākuIndekss]> kaudze[indekss]) { [kaudze[indekss], kaudze[vecākuIndekss]] = [kaudze[vecākuIndekss], kaudze[indekss]]; indekss = vecākuIndekss; parentIndex = Math.floor((indekss - 1) / 2); } } // Lietošanas piemērs const kaudze = []; const vērtības = [10, 7, 11, 5, 4, 13]; for (konst vērtību vērtība) { insertMinHeap(heap, value); console.log(`Ievietots ${value} minimālajā kaudzē: ${heap}`); }>
Izvade Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Laika sarežģītība: O(log(n)) ( kur n ir kaudzes elementu skaits )
Palīgtelpa: O(n)
2. Dzēšana Min-Heap datu struktūrā :
Mazākā elementa (saknes) noņemšana no minimālās kaudzes. Sakne tiek aizstāta ar pēdējo kaudzes elementu, un pēc tam kaudzes īpašība tiek atjaunota, nomainot jauno sakni ar tās mazāko atvasi, līdz vecākais ir mazāks par abiem bērniem vai līdz jaunā sakne sasniedz lapas mezglu.
- Aizstāt sakni vai elementu, kas jādzēš, ar pēdējo elementu.
- Izdzēsiet pēdējo elementu no kaudzes.
- Tā kā pēdējais elements tagad ir novietots saknes mezgla pozīcijā. Tātad tas var neatbilst kaudzes rekvizītam. Tāpēc salieciet pēdējo mezglu, kas novietots saknes vietā.
Ilustrācija :
Pieņemsim, ka kaudze ir minimālā kaudze, kā:
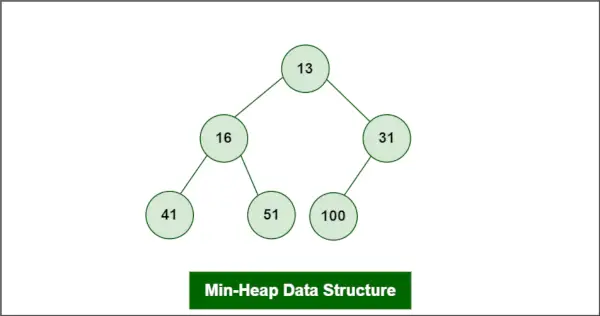
Minimālās kaudzes datu struktūra
Elements, kas jāizdzēš, ir root, t.i., 13.
Process :
Pēdējais elements ir 100.
tējkarote vs ēdamkarote
1. darbība: Aizstājiet pēdējo elementu ar sakni un izdzēsiet to.
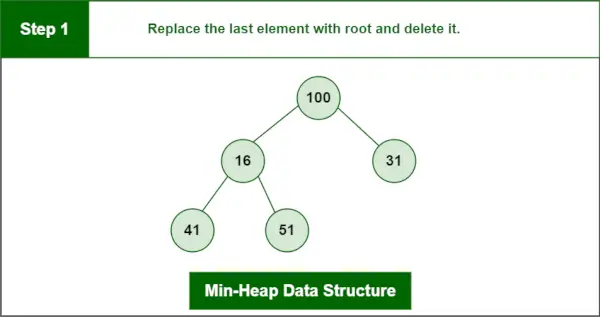
Minimālās kaudzes datu struktūra
2. darbība : Palielināt sakni.
Pēdējā kaudze:
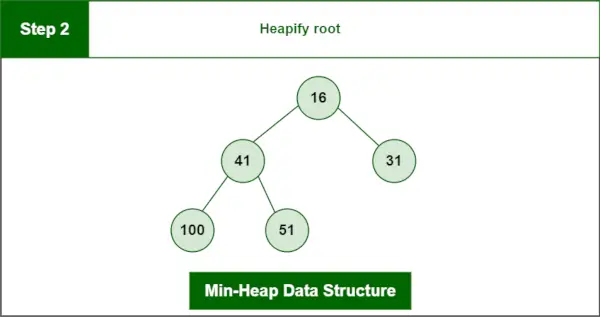
Minimālās kaudzes datu struktūra
Dzēšanas darbības ieviešana Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & kaudze, int vērtība) { // Pievienot jauno elementu kaudzes beigām.push_back(value); // Iegūstiet pēdējā elementa indeksu int index = heap.size() - 1; // Salīdziniet jauno elementu ar tā vecāku un apmainiet, ja // nepieciešams, kamēr (indekss> 0 && kaudze[(indekss - 1) / 2]> kaudze[indekss]) { swap(heap[indekss], kaudze[(indekss - 1) / 2]); // Pārvietot koku uz augšu uz pašreizējā // elementa vecāku // indeksa = (indekss - 1) / 2; } } // Funkcija mezgla dzēšanai no min-heap void delete_min_heap(vector & kaudze, int vērtība) { // Atrodiet dzēšamā elementa indeksu int index = -1; for (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector kaudze; int vērtības[] = {13, 16, 31, 41, 51, 100}; int n = lielums(vērtības) / lielums(vērtības[0]); for (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List kaudze, int vērtība) { // Pievienot jauno elementu kaudzes beigām. pievienot(vērtība); // Iegūstiet pēdējā elementa indeksu int index = heap.size() - 1; // Salīdziniet jauno elementu ar tā vecāku un apmainiet // ja nepieciešams, kamēr (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (indekss - 1) / 2); // Pārvietot koku uz augšu uz pašreizējā // elementa vecāku // indeksa = (indekss - 1) / 2; } } // Funkcija mezgla dzēšanai no minimālās kaudzes publiskā statiskā spēkā esamības deleteMinHeap(saraksts kaudze, int vērtība) { // Atrodi dzēšamā elementa indeksu int index = -1; for (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List kaudze = jauns ArrayList (); int[] vērtības = {13, 16, 31, 41, 51, 100}; int n = vērtības.garums; for (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 un kaudze[(indekss - 1) // 2]> kaudze[indekss]: kaudze[indekss], kaudze[(rādītājs - 1) // 2] = kaudze[(indekss - 1) // 2], kaudze[ indekss] indekss = (indekss - 1) // 2 def delete_min_heap(heap, value): indekss = -1 for i diapazonā(len(heap)): if kaudze[i] == vērtība: indekss = i break if index == -1: atgriešanās kaudze[indekss] = kaudze[-1] kaudze.pop(), savukārt True: kreisais_bērns = 2 * indekss + 1 labais_bērns = 2 * indekss + 2 mazākais = rādītājs, ja kreisais_bērns< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List kaudze = jauns saraksts (); public void Ievietot(int value) { kaudze.Pievienot(vērtība); int indekss = kaudze. Skaits - 1; while (indekss> 0 && kaudze[(indekss - 1) / 2]> kaudze[indekss]) { Swap(indekss, (indekss - 1) / 2); indekss = (indekss - 1) / 2; } } public void Dzēst(int vērtība) { int indekss = kaudze.IndekssOf(vērtība); if (indekss == -1) { return; } kaudze[indekss] = kaudze[kaudze.Skaits - 1]; kaudze.RemoveAt(heap.Count - 1); while (true) { int leftBērns = 2 * indekss + 1; int rightBērns = 2 * indekss + 2; int mazākais = indekss; ja (pa kreisiBērns< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && kaudze[flr]> kaudze[indekss]; flr = Math.floor((indeks - 1) / 2)) { [heap[index], heap[flr]] = [ kaudze[flr], kaudze[indekss], ]; // Pārvietot koku uz augšu uz pašreizējā elementa vecāku indeksu = Math.floor((indekss - 1) / 2); } } funkcija deleteMinHeap(heap, value) { // Atrodiet dzēšamā elementa indeksu let index = -1; for (lai i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));>
Izvade Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Laika sarežģītība : O(log n), kur n ir kaudzes elementu skaits
Palīgtelpa: O(n)
3. Min-Heap datu struktūras apskates darbība:
Lai piekļūtu minimālajam elementam (t.i., kaudzes saknei), tiek atgriezta saknes mezgla vērtība. Ielūkošanās laika sarežģītība min kaudzē ir O(1).
python jauna līnija
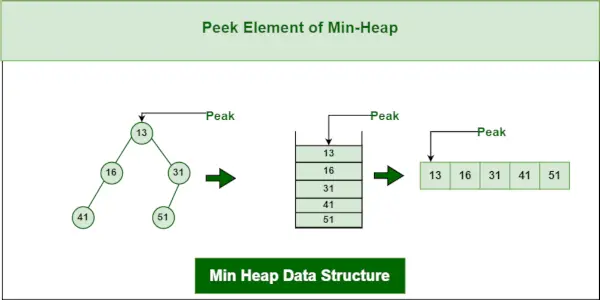
Minimālā kaudzes datu struktūra
Peek darbības ieviešana Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , lielāks > minHeap; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Iegūt maksimuma elementu (t.i., lielāko elementu) int peakElement = minHeap.top(); // Izdrukājiet pīķa elementa cout<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = new PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Iegūt maksimuma elementu (t.i., lielāko elementu) int peakElement = minHeap.peek(); // Drukāt maksimuma elementu System.out.println('Peak elements: ' + peakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Iegūt maksimuma elementu (t.i., mazāko elementu) int peakElement = minHeap.Peek(); // Izdrukājiet maksimuma elementu Console.WriteLine('Peak elements: ' + peakElement); } }> Javascript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Iegūt maksimuma elementu (t.i., mazāko elementu) const peakElement = minHeap.peek(); // Izdrukāt maksimuma elementu console.log(`Pīķa elements: ${peakElement}`);>>
Izvade Peak element: 1>
Laika sarežģītība : Minimālajā kaudzē, kas ieviests, izmantojot masīvu vai sarakstu, pīķa elementam var piekļūt konstantā laikā, O(1), jo tas vienmēr atrodas kaudzes saknē.
Minimālajā kaudzē, kas ieviesta, izmantojot bināro koku, pīķa elementam var piekļūt arī O(1) laikā, jo tas vienmēr atrodas koka saknē.
Palīgtelpa: O(n)
4. Heapify darbība Min-Heap datu struktūrā:
Lai izveidotu minimālo kaudzi no nešķirota masīva, var izmantot kaudzes palielināšanas darbību. Tas tiek darīts, sākot no pēdējā mezgla, kas nav lapas, un atkārtoti veicot burbuļu lejupvērsšanas darbību, līdz visi mezgli atbilst kaudzes īpašībai.
Heapify operācija Min Heap
Heapify operācijas ieviešana Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int mazākais = i; int l = 2*i + 1; int r = 2*i + 2; ja (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Pieņemsim, ka sakne sākotnēji ir mazākais elements int mazākais = i; // Aprēķināt pašreizējā mezgla kreisā un labā bērna indeksus int l = 2 * i + 1; int r = 2 * i + 2; // Salīdziniet kreiso bērnu ar pašreizējo mazāko if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Sākotnējais masīvs: '); // Drukāt sākotnējo masīvu (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Heap pēc kaudzes veidošanas darbības: '); // Drukāt minimālo kaudzi pēc kaudzes veidošanas operācijas (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int mazākais = i; int pa kreisi = 2 * i + 1; int pa labi = 2 * i + 2; // Salīdziniet kreiso bērnu ar pašreizējo mazāko mezglu. ja (pa kreisi< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = jauns saraksts {10, 5, 15, 2, 20, 30}; Console.Write('Sākotnējais masīvs: '); foreach (int num in arr) Console.Write(num + ' '); // Veikt kaudzes palielināšanas darbību min-heap. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap pēc kaudzes veidošanas darbības: '); foreach (int num in arr) Console.Write(num + ' '); } }> Javascript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length); // Drukāt min-heap pēc kaudzes veidošanas darbības console.log('Min-Heap pēc kaudzes veidošanas darbības: ' + arr.join(' ')); } // Izsauciet galveno funkciju, lai sāktu procesu main();>>
Izvade Kaudzes laika sarežģītība min kaudzē ir O(n). 5. Meklēšanas darbība Min-Heap datu struktūrā:
Lai meklētu elementu minimālajā kaudzē, var veikt lineāru meklēšanu masīvā, kas attēlo kaudzi. Tomēr lineārās meklēšanas laika sarežģītība ir O (n), kas nav efektīva. Tāpēc meklēšana nav bieži izmantota darbība min kaudzē.
Šeit ir koda piemērs, kas parāda, kā meklēt elementu min kaudzē, izmantojot std::find() :
C++ #include using namespace std; int main() { priority_queue , lielāks > min_heap; // piemērs max kaudze min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int elements = 6; // elements, lai meklētu būtību atrasts = false; // Kopējiet minimālo kaudzi pagaidu rindā un meklējiet // elementu std::priority_queue , lielāks > temp = min_kaudze; while (!temp.empty()) { if (temp.top() == elements) { atrasts = true; pārtraukums; } temp.pop(); } if (atrasts) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = new PriorityQueue(); min_heap.add(3); // ievietot elementus prioritārajā rindā min_heap.offer(1); min_heap.offer(4); min_heap.offer(1); min_heap.offer(6); int elements = 6; // elements, lai meklētu Būla atrasts = false; // Kopējiet minimālo kaudzi pagaidu rindā un meklējiet // elementu PriorityQueue temp = new PriorityQueue(min_heap); while (!temp.isEmpty()) { if (temp.poll() == elements) { atrasts = true; pārtraukums; } } if (atrasts) { System.out.println( 'Elements atrasts min kaudzē.'); } else { System.out.println( 'Elements nav atrasts min kaudzē.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // piemērs min kaudze minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); int elements = 6; // elements, lai meklētu būtību atrasts = false; // Kopējiet minimālo kaudzi pagaidu rindā un meklējiet // elementu var temp = new PriorityQueue (minHeap); while (temp.Count> 0) { if (temp.Peek() == elements) { found = true; pārtraukums; } temp.Dequeue(); } if (atrasts) { Console.WriteLine( 'Elements atrasts min kaudzē.'); } else { Console.WriteLine( 'Elements nav atrasts min kaudzē.'); } } }> Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == elements) { atrasts = true; pārtraukums; } temp.dequeue(); } if (atrasts) { console.log('Elements atrasts min kaudzē.'); } else { console.log('Elements nav atrasts min kaudzē.'); }>
Izvade The laika sarežģītība no šīs programmas ir O(n log n) , kur n ir prioritārās rindas elementu skaits. Ievietošanas darbībai ir laika sarežģītība O(log n) sliktākajā gadījumā, jo kaudzes īpašums ir jāuztur. Meklēšanas darbība ietver prioritārās rindas kopēšanu pagaidu rindā un pēc tam pagaidu rindas šķērsošanu, kas aizņem O(n log n) laiks sliktākajā gadījumā, jo katrs elements ir jākopē un jāizņem no rindas, un prioritārā rinda ir jāpārveido katrai darbībai.
The telpas sarežģītība no programmas ir O(n) jo tas uzglabā n elementi prioritārajā rindā un izveido pagaidu rindu ar n elementi.
Min-Heap datu struktūras pielietojumi:
- Kaudzes kārtošana: Minimālā kaudze tiek izmantota kā galvenā sastāvdaļa kaudzes kārtošanas algoritmā, kas ir efektīvs kārtošanas algoritms ar laika sarežģītību O(nlogn).
- Prioritātes rinda: Prioritātes rindu var ieviest, izmantojot minimālās kaudzes datu struktūru, kurā elements ar minimālo vērtību vienmēr atrodas saknē.
- Dijkstra algoritms: Dijkstra algoritmā min kaudze tiek izmantota, lai saglabātu grafa virsotnes ar minimālo attālumu no sākuma virsotnes. Virsotne ar minimālo attālumu vienmēr atrodas kaudzes saknē.
- Hafmena kodēšana: Hafmena kodēšanā minimālā kaudze tiek izmantota, lai ieviestu prioritāro rindu, lai izveidotu optimālu prefiksa kodu noteiktai rakstzīmju kopai.
- Apvienot K sakārtotos masīvus: Ņemot vērā K sakārtotus masīvus, mēs varam tos efektīvi apvienot vienā sakārtotā masīvā, izmantojot minimālo kaudzes datu struktūru.
Minimālās kaudzes datu struktūras priekšrocības:
- Efektīva ievietošana un dzēšana : Minimālā kaudze ļauj ātri ievietot un dzēst elementus ar laika sarežģītību O(log n), kur n ir kaudzes elementu skaits.
- Efektīva minimālā elementa izguve: Minimālais elements min kaudzē vienmēr atrodas kaudzes saknē, ko var izgūt O(1) laikā.
- Kosmosa efektīva: Minimālā kaudze ir kompakta datu struktūra, ko var ieviest, izmantojot masīvu vai bināro koku, kas padara to telpas efektīvu.
- Kārtošana: Minimālo kaudzi var izmantot, lai ieviestu efektīvu kārtošanas algoritmu, piemēram, kaudzes kārtošanu ar laika sarežģītību O(n log n).
- Prioritātes rinda: Minimālo kaudzi var izmantot, lai ieviestu prioritātes rindu, kur elementu ar minimālo prioritāti var efektīvi izgūt O(1) laikā.
- Daudzpusība: Min kaudzītei ir vairākas lietojumprogrammas datorzinātnēs, tostarp grafiku algoritmi, datu saspiešana un datu bāzu sistēmas.
Kopumā min kaudze ir noderīga un daudzpusīga datu struktūra, kas piedāvā efektīvas darbības, telpas efektivitāti un tai ir vairākas lietojumprogrammas datorzinātnēs.




