Kvadrants ir definēts kā apgabals telpā, kas ir sadalīts četrās vienādās daļās ar divām asīm, proti, X-asi un Y-asi Dekarta plaknē. Šīs divas asis krustojas viena ar otru 90 grādu leņķī, un šādi izveidotos četrus apgabalus sauc par četriem kvadrantiem, proti, I kvadrants, II kvadrants, III kvadrants un IV kvadrants.
hrithik roshan
Šajā rakstā mēs izpētīsim svarīgākos kvadrantu jēdzienus, tostarp to, kas ir kvadrants, tā laukumu, kvadrantu grafiku, Dekarta plakni, zīmju konvencijas kvadrantā, abscisu un koordinātu, kā arī punktu zīmēšanu kvadrantā.
Satura rādītājs
- Kas ir grafika kvadranti?
- Paraksti konvenciju kvadrantos
- Punktu uzzīmēšana kvadrantos
- Trigonometriskās vērtības dažādos kvadrantos
Kas ir grafika kvadranti?
Kvadrants ir noteikta vieta uz a Dekarta plakne , ko rada X un Y asu krustpunkts. Šajā plaknē veidojas četri kvadranti, katrs ar savām unikālajām iezīmēm. Pirmajā kvadrantā, kas atrodas augšējā labajā stūrī, ir pozitīvas x un y koordinātas. Otrajā kvadrantā, kas atrodas augšējā kreisajā stūrī, ir negatīvas x un pozitīvas y koordinātas utt. Šo kvadrantu izpratne ir būtiska, lai grafikā noteiktu un interpretētu punktus, nodrošinot sistemātisku veidu, kā pārvietoties un analizēt Dekarta koordinātas.
4 kvadranti koordinātu plaknē
Dekarta plakne, ko veido X un Y asis, ir sadalīta četros kvadrantos, kuriem katram ir atšķirīgas īpašības:
- Pirmais kvadrants: Atrodas augšējā labajā stūrī, gan x, gan y koordinātas ir pozitīvas. Šis kvadrants attēlo punktus plaknes augšējā labajā daļā.
- Otrais kvadrants: Atrodas augšējā kreisajā stūrī, x-koordināta ir negatīva, bet y-koordināta ir pozitīva. Šis kvadrants aptver punktus plaknes augšējā kreisajā daļā.
- Trešais kvadrants: Apakšējā kreisajā stūrī gan x, gan y koordinātas ir negatīvas. Punkti plaknes apakšējā kreisajā apgabalā ietilpst šajā kvadrantā.
- Ceturtais kvadrants: Apakšējā labajā stūrī ir x-koordināta, kas ir pozitīva, un y-koordināta ir negatīva. Šajā kvadrantā ir ietverti punkti plaknes apakšējā labajā pusē.
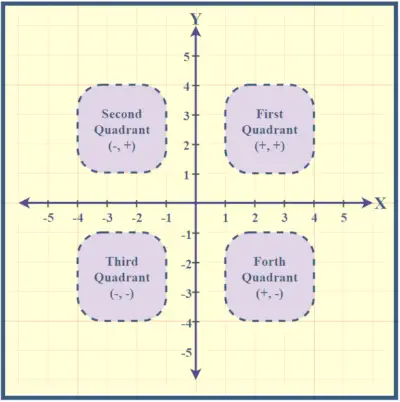
Kvadranti ir numurēti pretēji pulksteņrādītāja virzienam, sākot no augšējā labās puses. Punktu, kur krustojas X un Y asis, sauc par sākumpunktu ar koordinātām (0,0), kas norāda nulles vērtības gan x, gan y. Šo kvadrantu izpratne palīdz atrast punktus Dekarta plaknē.
Kas ir izcelsme?
Diagrammas sākuma punkts, kas pazīstams kā sākumpunkts un parādīts kā (0, 0), ir vieta, kur krustojas horizontālā x ass un vertikālā y ass. Tas nozīmē, ka sākumā gan x, gan y vērtības ir nulle. Tas kalpo kā atskaites punkts citu punktu atrašanai grafikā. Iepriekš pievienotajā attēlā punkts O parāda izcelsmi.
Abscisa un ordināta kvadrantos
Četros kvadrantos skaitļi ir attēloti kā pāri (a, b), kur “a” apzīmē x koordinātu un “b” apzīmē y koordinātu. Lai noskaidrotu, kur atrodas punkts bez diagrammas, pievērsiet uzmanību x-koordinātas (abscisas) un y-koordinātas (ordinātas) zīmēm. Piemēram, ja jums ir tāds punkts kā Q (3, -5), zīmes (+ve, -ve) norāda, ka tas atrodas IV kvadrantā.
Abscisa parāda horizontālo attālumu no Y ass. Pozitīva abscisa nozīmē pa labi, un mūsu piemērā abscisa = 3 nozīmē virzīties pa labi no sākuma pa x asi par 3 vienībām.
Ordinātas norāda vertikālo attālumu no sākuma. Negatīvā ordināta nozīmē iet uz leju no sākuma pa y asi. Piemērā ordināta = -5 nozīmē samazināties par 5 vienībām.
Paraksti konvenciju kvadrantos
Zīmju konvencijas kvadrantos var viegli saprast, izmantojot tālāk pievienoto attēlu,

XY plaknē, virzoties no kreisās puses uz labo pa x asi, x-koordināta palielinās. Tāpat pa y asi, virzoties no apakšas uz augšu, palielinās y koordināte. XY plakne ir sadalīta četros kvadrantos, katrā no kuriem ir noteiktas x un y koordinātu zīmju vienošanās:
| Kvadrants | x-koordināta | y-koordināta |
|---|---|---|
| 1. kvadrants | Pozitīvs (+) | Pozitīvs (+) |
| 2. kvadrants | Negatīvs (-) | Pozitīvs (+) |
| 3. kvadrants | Negatīvs (-) | Negatīvs (-) |
| 4. kvadrants | Pozitīvs (+) | Negatīvs (-) |
Tāpēc 1. kvadranta punktiem ir pozitīvas vērtības gan x, gan y, 2. kvadrantā ir negatīvs x un pozitīvs y, 3. kvadrantā ir gan negatīvas x, gan y vērtības, bet 4. kvadrantā ir pozitīvs x un y. negatīvs y.
Punktu uzzīmēšana kvadrantos
Dekarta plaknē punkti tiek identificēti ar x asi un y asi. Šie punkti ir apzīmēti kā (a, b), kur “a” ir x-koordināta (abscisa), bet “b” ir y-koordināta (ordināta). Lai novietotu punktu kvadrantā, mēs ņemam vērā šo koordinātu zīmes. X un y vērtības norāda, cik tālu punkts atrodas attiecīgi no x ass un y ass.
Piemēram, uzzīmējiet punktu (2, -5) Dekarta plaknē. Analizējot koordinātu zīmi, atklājas, ka punkts atrodas 4. kvadrantā. Tas būs 2 vienību attālumā no x ass (pa labi) un 5 vienības attālumā no y ass (uz leju), kā atskaites punktu izmantojot sākumpunktu.
Trigonometriskās vērtības dažādos kvadrantos
Dažādas vērtības trigonometriskās funkcijas dažādos kvadrantos var uzzināt, izpētot tālāk pievienoto tabulu kā
| Kvadrants | Bez | Cos | Tātad | Kosekants | Sekants | Kotangenss |
|---|---|---|---|---|---|---|
| 1. kvadrants | + Imessage spēles ar Android | + | + | + | + | + |
| 2. kvadrants | + | – | + | + | – | – |
| 3. kvadrants | – | – | – | – | – | + |
| 4. kvadrants | – | – | – | – | + | – |
1. kvadrantā visas trigonometriskās attiecības ir pozitīvas. 2. kvadrantā sine un kosekants ir pozitīvi (+), bet kosinuss un sekants ir negatīvi (-). 3. kvadrantā Tangenss un Kotangenss ir pozitīvi (+), bet kosinuss un sekants ir negatīvi (-). 4. kvadrantā Sine un Cosecant ir negatīvi (-), savukārt kosinuss un sekants ir pozitīvi (+).
Lasīt vairāk,
- Koordinātu ģeometrija
- Paralēlas līnijas
- Distances formula
Atrisināti piemēri kvadrantā
1. piemērs. Uzzīmējiet punktu A (3, -4) un identificējiet tā kvadrantu.
Risinājums:
Punkts A atrodas pie koordinātām (3, -4). Tā kā x-koordināta ir pozitīva (3) un y-koordināta ir negatīva (-4), punkts A atrodas IV kvadrantā.
veiksmi
2. piemērs. Uzzīmējiet punktu P (-5, 2) un nosakiet tā kvadrantu
Risinājums:
Punkta P koordinātas ir (-5, 2). Lai noteiktu kvadrantu, mēs pārbaudām x un y koordinātu zīmes.
X-koordināta ir -5, kas norāda pozīciju pa kreisi no sākuma.
Y-koordināta ir 2, kas norāda pozīciju virs sākuma.
Tāpēc, tā kā x-koordināta ir negatīva un y-koordināta ir pozitīva, punkts P atrodas II kvadrantā.
Punkts P (-5, 2) atrodas Dekarta plaknes II kvadrantā.
Prakses problēmas kvadrantos
1. problēma: Uzzīmējiet punktu (1, -1) un identificējiet tā kvadrantu.
2. problēma: Atrodiet trīs punktus uz x ass un nosakiet to kvadrantus.
3. problēma: Ja punkts atrodas uz y ass ar koordinātām (0, -3), kurā kvadrantā tas atrodas?
4. problēma: Atrodiet punktus Q (2, 2), R (-2, -2) un S (0, 0) un pārbaudiet kolinearitāti.
5. problēma: Uzzīmējiet punktu (-4, -3) un paskaidrojiet, kurā kvadrantā tas atrodas.
Bieži uzdotie jautājumi par kvadrantiem
1. Kas ir kvadrants matemātikā?
Matemātikā kvadrants ir viena no četrām sekcijām, kas izveidota, krustojoties divām perpendikulārām taisnēm vai asis. Šīs asis Dekarta koordinātu sistēmā parasti tiek apzīmētas kā x-ass un y-ass.
2. Kā sauc divu asu krustpunktu?
Divu asu krustpunktu Dekarta koordinātu sistēmā sauc par sākumpunktu. To attēlo x ass un y ass saskares punkts, ko parasti apzīmē kā (0,0).
3. Kas ir 4 kvadranti?
Četri kvadranti ir sekcijas, kas izveidotas, sadalot Dekarta koordinātu plakni četrās vienādās daļās. Tie ir apzīmēti kā pirmais kvadrants (Q1), otrais kvadrants (Q2), trešais kvadrants (Q3) un ceturtais kvadrants (Q4).
4. Kurš kvadrants ir pozitīvs?
Pozitīvais kvadrants Dekarta koordinātu sistēmā ir pirmais kvadrants (Q1). Šajā kvadrantā gan x, gan y koordinātas ir pozitīvas.
5. Kāda ir kvadrantu izmantošana grafikos?
Kvadranti grafikos nodrošina sistemātisku veidu, kā organizēt un atrast punktus, pamatojoties uz to koordinātām. Tie palīdz vizualizēt attiecības starp mainīgajiem un analizēt modeļus datu kopās, atvieglojot grafisko attēlojumu interpretāciju.
6. Kuram kvadrantam ir abas Koordinātas Pozitīvas vērtības?
Pirmais kvadrants (Q1) ir kvadrants, kurā gan punktu x, gan y koordinātas ir pozitīvas. Tas ir vienīgais kvadrants ar abām pozitīvajām vērtībām.
7. Kādi ir 4 apļa kvadranti?
Kvadrantu jēdziens nav tieši attiecināms uz apļiem. Tā vietā apļi tiek sadalīti leņķos, ko mēra grādos. Tomēr, ja attiecas uz apļveida sektoriem, var izmantot tādus terminus kā pirmais sektors, otrais sektors, trešais sektors un ceturtais sektors, kas atbilst dažādiem leņķiskajiem reģioniem.
