IEVADS CIRCULAR LINKED LIST

Kas ir Circular saistītais saraksts?

The apļveida saistīto sarakstu ir saistīts saraksts, kurā visi mezgli ir savienoti, veidojot apli. Apļveida saistītā sarakstā pirmais mezgls un pēdējais mezgls ir savienoti viens ar otru, kas veido apli. Beigās nav NULL.

Apļveida saistīts saraksts

Parasti ir divu veidu cirkulāri saistīti saraksti:

jvm

Apļveida, atsevišķi saistīts saraksts: Apļveida Atsevišķi saistītā sarakstā saraksta pēdējā mezglā ir rādītājs uz saraksta pirmo mezglu. Mēs šķērsojam apļveida, atsevišķi saistīto sarakstu, līdz sasniedzam to pašu mezglu, no kura sākām. Apļveida, atsevišķi saistītajam sarakstam nav ne sākuma, ne beigu. Neviena mezgla nākamajā daļā nav nulles vērtības.

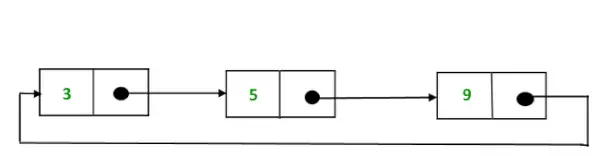
Circular atsevišķi saistītā saraksta attēlojums

Apļveida divreiz saistīts saraksts: Circular Duubly Linked List ir gan divkārši saistīta saraksta, gan apļveida saistītā saraksta īpašības, kurā divi secīgi elementi ir saistīti vai savienoti ar iepriekšējo un nākamo rādītāju, un pēdējais mezgls norāda uz pirmo mezglu ar nākamo rādītāju, un arī pirmais mezgls norāda uz pēdējais mezgls ar iepriekšējo rādītāju.

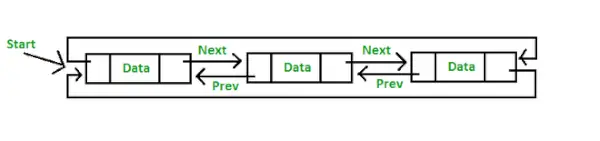
Apļveida, divkārši saistīta saraksta attēlojums

Piezīme: Mēs izmantosim atsevišķi apļveida saistīto sarakstu, lai attēlotu apļveida saistītā saraksta darbību.

Apļveida saistītā saraksta attēlojums:

Apļveida saistītie saraksti ir līdzīgi atsevišķiem saistītajiem sarakstiem, izņemot pēdējo mezglu savienošanu ar pirmo mezglu.

Apļveida saistītā saraksta mezgla attēlojums:

C++

 // Class Node, similar to the linked list class Node{  int value; // Points to the next node.  Node next; }>

 struct Node {  int data;  struct Node *next; };>

Java

 public class Node {  int data;  Node next;    public Node(int data) {  this.data = data;  this.next = null;  } }>

 public class Node {  public int data;  public Node next;    public Node(int data)  {  this.data = data;  this.next = null;  } }>

Javascript

 class Node {  constructor(data) {  this.data = data;  this.next = null;  } }>

PHP

 class Node {  public $data;  public $next;  function __construct($data) {  $this->dati = $dati;  $šis->nākamais = null;  } }>

Python3

 # Class Node, similar to the linked list class Node: def __init__(self,data): self.data = data self.next = None>

Circular atsevišķi saistītā saraksta piemērs:

Apļveida saistītā saraksta piemērs

Iepriekš minēto apļveida sarakstu var attēlot kā:

C++

 // Initialize the Nodes. Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>

Node* one = createNode(3); Node* two = createNode(5); Node* three = createNode(9); // Connect nodes one->nākamais = divi; divi->nākamie = trīs; trīs->nākamais = viens;>>Java Node one = new Node(3); Node two = new Node(5); Node three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
 Javascript let one = new Node(3); let two = new Node(5); let three = new Node(9); // Connect nodes one.next = two; two.next = three; three.next = one;>
 PHP $one = new Node(3); $two = new Node(5); $three = new Node(9); // Connect nodes $one->nākamais = $ divi; $divi->nākamais = $trīs; $trīs->nākamais = $viens;>>Python3    Paskaidrojums:    Iepriekš minētajā programmā viens, divi un trīs ir mezgli ar attiecīgi vērtībām 3, 5 un 9, kas ir savienoti apļveida veidā kā:
     Node One:    Nākamais rādītājs saglabā otrā mezgla adresi.
    Otrajam mezglam:    Nākamais saglabā trešā mezgla adresi
    Trešajam mezglam:    The         Nākamais norāda uz mezglu viens.
Darbības apļveida saistītajā sarakstā:
Mēs varam veikt dažas darbības ar apļveida saistīto sarakstu, kas ir līdzīgas atsevišķi saistītajam sarakstam, un tās ir:
 Ievietošana
Dzēšana
1. Ievietošana apļveida saistītajā sarakstā: 
Mezglu var pievienot trīs veidos:
 Ievietošana saraksta sākumā
Ievietošana saraksta beigās
Ievietošana starp mezgliem
1)    Ievietošana saraksta sākumā:    Lai saraksta sākumā ievietotu mezglu, veiciet šīs darbības:
 Izveidojiet mezglu, sakiet T.
Padarīt T -> nākamais = pēdējais -> nākamais.
pēdējais -> nākamais = T.
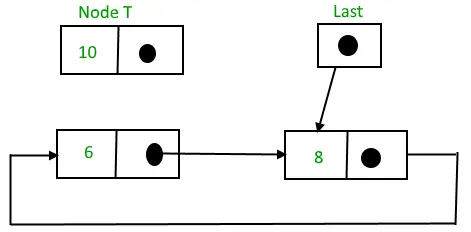
  Apļveida saistīts saraksts pirms ievietošanas
 Un tad,
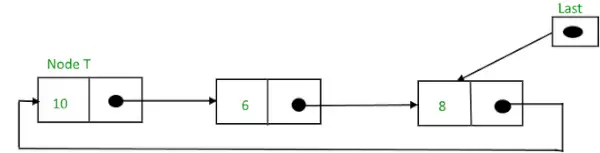
  Apļveida saistīts saraksts pēc ievietošanas
 2)    Ievietojums saraksta beigās:    Lai saraksta beigās ievietotu mezglu, rīkojieties šādi:
 Izveidojiet mezglu, sakiet T.
Make T -> nākamais = pēdējais -> nākamais;
pēdējais -> nākamais = T.
pēdējais = T.
Pirms ievietošanas,
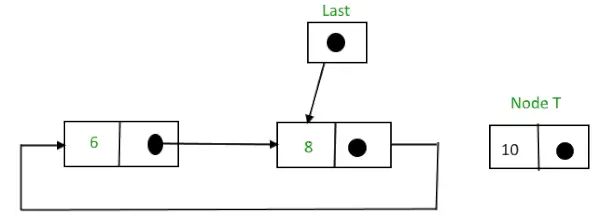
  Apļveida saistīts saraksts pirms mezgla ievietošanas beigās
 Pēc ievietošanas,
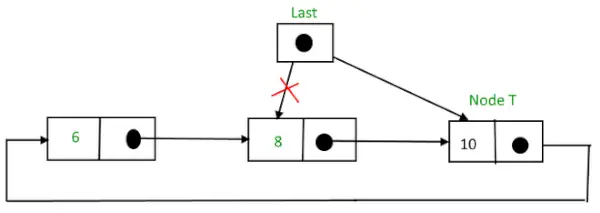
  Apļveida saistīts saraksts pēc mezgla ievietošanas beigās
 3)    Ievietošana starp mezgliem:    Lai starp abiem mezgliem ievietotu mezglu, veiciet šīs darbības:
 Izveidojiet mezglu, sakiet T.
Atrodiet mezglu, pēc kura jāievieto T, sakiet, ka mezgls ir P.
Make T -> next = P -> next;
P -> nākamais = T.
Pieņemsim, ka 12 ir jāievieto pēc tam, kad mezglam ir vērtība 10,
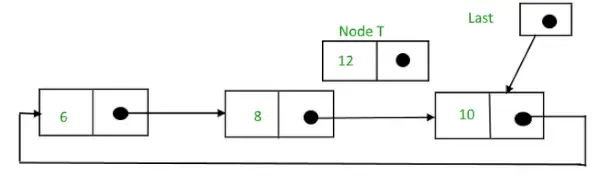
  Apļveida saistīts saraksts pirms ievietošanas
 Pēc meklēšanas un ievietošanas
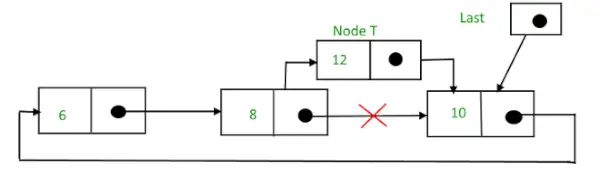
  Apļveida saistīts saraksts pēc ievietošanas
 2. Dzēšana apļveida saistītā sarakstā:
    1) Dzēsiet mezglu tikai tad, ja tas ir vienīgais mezgls apļveida saitīšanas sarakstā:    
 Atbrīvojiet mezgla atmiņu
Pēdējai vērtībai jābūt NULL Mezgls vienmēr norāda uz citu mezglu, tāpēc NULL piešķiršana nav nepieciešama.  
Kā sākumpunktu var iestatīt jebkuru mezglu.  
Mezgli tiek ātri šķērsoti no pirmā līdz pēdējam.
    2) Pēdējā mezgla dzēšana:    
 Atrodiet mezglu pirms pēdējā mezgla (lai tas būtu temp)
Saglabājiet mezgla adresi blakus pēdējam mezglam temp
Izdzēsiet pēdējo atmiņu
Beigās ielieciet temperatūru
    3) Izdzēsiet jebkuru mezglu no apļveida saistītā saraksta:    Mums tiks piešķirts mezgls, un mūsu uzdevums ir dzēst šo mezglu no apļveida saistītā saraksta.
     Algoritms:     
    1. gadījums    : saraksts ir tukšs.
 Ja saraksts ir tukšs, mēs vienkārši atgriezīsimies.
    2. gadījums    : Saraksts nav tukšs
 Ja saraksts nav tukšs, mēs definējam divus rādītājus    curr    un    iepriekj    un inicializējiet rādītāju    curr    Ar    galvu    mezgls.
Pārvietojiet sarakstu, izmantojot    curr    lai atrastu dzēšamo mezglu un pirms pārejas uz curr uz nākamo mezglu, katru reizi iestatiet prev = curr.
Ja mezgls ir atrasts, pārbaudiet, vai tas ir vienīgais mezgls sarakstā. Ja jā, iestatiet head = NULL un free(curr).
Ja sarakstā ir vairāk nekā viens mezgls, pārbaudiet, vai tas ir saraksta pirmais mezgls. Nosacījums, lai to pārbaudītu (curr == galva). Ja jā, tad pārvietojiet iepriekšējo, līdz tas sasniedz pēdējo mezglu. Kad iepriekšējais ir sasniedzis pēdējo mezglu, iestatiet head = head -> next un prev -> next = head. Dzēst curr.
Ja curr nav pirmais mezgls, mēs pārbaudām, vai tas ir pēdējais mezgls sarakstā. Nosacījums, lai to pārbaudītu, ir (curr -> next == head).
Ja curr ir pēdējais mezgls. Iestatiet iepriekšējo -> nākamo = head un izdzēsiet mezglu curr ar free(curr).
Ja dzēšamais mezgls nav ne pirmais, ne pēdējais mezgls, iestatiet prev -> next = curr -> next un dzēsiet curr.
Ja mezgls sarakstā nav iekļauts, atgrieziet galvu un nedariet neko.
Tālāk ir norādīta iepriekš minētās pieejas ieviešana.
C++ // C++ program to delete a given key from // linked list. #include  using namespace std; // Structure for a node class Node { public:  int data;  Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(Node** head_ref, int data) {  // Create a new node and make head  // as next of it.  Node* ptr1 = new Node();  ptr1->dati = dati;  ptr1->nākamais = *head_ref;  // Ja saistītais saraksts nav NULL, tad // iestatiet nākamo no pēdējā mezgla if (*head_ref != NULL) { // Atrodiet mezglu pirms galvas un // atjauniniet nākamo mezglu.  Mezgls* temp = *head_ref;  while (temp->next != *head_ref) temp = temp->next;  temp->nākamais = ptr1;  } else // Pirmajam mezglam ptr1->next = ptr1;  *head_ref = ptr1; } // Funkcija mezglu drukāšanai dotajā // cirkulāri saistītā sarakstā void printList(Node* head) { Node* temp = head;  if (galva != NULL) { do { cout<< temp->datus<< ' ';  temp = temp->Nākamais;  } while (temp != galva);  } cout<< endl; } // Function to delete a given node // from the list void deleteNode(Node** head, int key) {  // If linked list is empty  if (*head == NULL)  return;  // If the list contains only a  // single node  if ((*head)->dati == taustiņš && (*galva)->nākamais == *galva) { free(*head);  *galva = NULL;  atgriešanās;  } Mezgls *pēdējais = *galva, *d;  // Ja head ir jāizdzēš if ((*head)->data == taustiņš) { // Atrodiet saraksta pēdējo mezglu while (pēdējais->nākamais != *head) pēdējais = pēdējais->nākamais;  // Norādīt pēdējo mezglu uz nākamo // head t.i., saraksta otro mezglu // pēdējais->nākamais = (*head)->next;  brīvs(*galva);  *galva = pēdējais->nākamais;  atgriešanās;  } // Vai nu dzēšamais mezgls // nav atrasts vai saraksta beigas // nav sasniegts, kamēr (pēdējais->nākamais != *head && pēdējais->nākamais->dati != taustiņš) { pēdējais = pēdējais ->nākamais;  } // Ja tika atrasts dzēšamais mezgls if (pēdējais->nākamais->dati == atslēga) { d = pēdējais->nākamais;  pēdējais->nākamais = d->nākamais;  bezmaksas(d);  } cits cout<< 'Given node is not found in the list!!!
'; } // Driver code int main() {  // Initialize lists as empty  Node* head = NULL;  // Created linked list will be  // 2->5->7->8->10 push (&galva, 2);  push(&galva, 5);  push(&galva, 7);  push(&galva, 8);  push(&galva, 10);  cout<< 'List Before Deletion: ';  printList(head);  deleteNode(&head, 7);  cout << 'List After Deletion: ';  printList(head);  return 0; }>
 C #include  #include  // Structure for a node struct Node {  int data;  struct Node* next; }; // Function to insert a node at the // beginning of a Circular linked list void push(struct Node** head_ref, int data) {  // Create a new node and make head  // as next of it.  struct Node* ptr1 = (struct Node*)malloc(sizeof(struct Node));  ptr1->dati = dati;  ptr1->nākamais = *head_ref;  // Ja saistītais saraksts nav NULL, tad // iestatiet nākamo no pēdējā mezgla if (*head_ref != NULL) { // Atrodiet mezglu pirms galvas un // atjauniniet nākamo mezglu.  struct Node* temp = *head_ref;  while (temp->next != *head_ref) temp = temp->next;  temp->nākamais = ptr1;  } else // Pirmajam mezglam ptr1->next = ptr1;  *head_ref = ptr1; } // Funkcija mezglu drukāšanai dotajā // cirkulāri saistītā sarakstā void printList(struct Node* head) { struct Node* temp = head;  if (head != NULL) { do { printf ('%d ', temp-> data);  temp = temp->nākamais;  } while (temp != galva);  } printf('
'); } // Dotā mezgla dzēšanas funkcija // no saraksta void deleteNode(struct Node** head, int key) { // Ja saistītais saraksts ir tukšs if (*head == NULL) return;  // Ja sarakstā ir tikai // viens mezgls if ((*head)->data == taustiņš && (*head)->next == *head) { free(*head);  *galva = NULL;  atgriešanās;  } struct Node *pēdējais = *galva, *d;  // Ja head ir jāizdzēš if ((*head)->data == taustiņš) { // Atrodiet saraksta pēdējo mezglu while (pēdējais->nākamais != *head) pēdējais = pēdējais->nākamais;  // Norādīt pēdējo mezglu uz nākamo // head t.i., saraksta otro mezglu // pēdējais->nākamais = (*head)->next;  brīvs(*galva);  *galva = pēdējais->nākamais;  atgriešanās;  } // Vai nu dzēšamais mezgls // nav atrasts vai saraksta beigas // nav sasniegts, kamēr (pēdējais->nākamais != *head && pēdējais->nākamais->dati != taustiņš) { pēdējais = pēdējais ->nākamais;  } // Ja tika atrasts dzēšamais mezgls if (pēdējais->nākamais->dati == atslēga) { d = pēdējais->nākamais;  pēdējais->nākamais = d->nākamais;  bezmaksas(d);  } else printf('Dotais mezgls sarakstā nav atrasts!!!
'); } // Draivera kods int main() { // Inicializēt sarakstus kā tukšu struktūru Node* head = NULL;  // Izveidotais saistītais saraksts būs // 2->5->7->8->10 push(&head, 2);  push(&galva, 5);  push(&galva, 7);  push(&galva, 8);  push(&galva, 10);  printf('Saraksts pirms dzēšanas: ');  drukas saraksts(galva);  deleteNode(&head, 7);  printf('Saraksts pēc dzēšanas: ');  drukas saraksts(galva);  atgriezties 0; }>
 Java // Java program to delete a given key from // linked list. import java.io.*; import java.util.*; public class GFG {  /* structure for a node */  static class Node {  int data;  Node next;  };  /* Function to insert a node at the beginning of a Circular linked list */  static Node push(Node head_ref, int data)  {  // Create a new node and make head as next  // of it.  Node ptr1 = new Node();  ptr1.data = data;  ptr1.next = head_ref;  /* If linked list is not null then set the next of last node */  if (head_ref != null) {  // Find the node before head and update  // next of it.  Node temp = head_ref;  while (temp.next != head_ref)  temp = temp.next;  temp.next = ptr1;  }  else  ptr1.next = ptr1; /*For the first node */  head_ref = ptr1;  return head_ref;  }  /* Function to print nodes in a given circular linked list */  static void printList(Node head)  {  Node temp = head;  if (head != null) {  do {  System.out.printf('%d ', temp.data);  temp = temp.next;  } while (temp != head);  }  System.out.printf('
');  }  /* Function to delete a given node from the list */  static Node deleteNode(Node head, int key)  {  if (head == null)  return null;  int flag = 0;  // Find the required node  Node curr = head, prev = new Node();  while (curr.data != key) {  if (curr.next == head) {  System.out.printf(  'Given node is not found in the list!!!
');  flag = 1;  break;  }  prev = curr;  curr = curr.next;  }  // Check if the element is not present in the list  if (flag == 1)  return head;  // Check if node is only node  if (curr == head && curr.next == head) {  head = null;  return head;  }  // If more than one node, check if  // it is first node  if (curr == head) {  prev = head;  while (prev.next != head)  prev = prev.next;  head = curr.next;  prev.next = head;  }  // check if node is last node  else if (curr.next == head) {  prev.next = head;  }  else {  prev.next = curr.next;  }  return head;  }  /* Driver code */  public static void main(String args[])  {  /* Initialize lists as empty */  Node head = null;  /* Created linked list will be 2.5.7.8.10 */  head = push(head, 2);  head = push(head, 5);  head = push(head, 7);  head = push(head, 8);  head = push(head, 10);  System.out.printf('List Before Deletion: ');  printList(head);  head = deleteNode(head, 7);  System.out.printf('List After Deletion: ');  printList(head);  } } // This code is contributed by Susobhan Akhuli>
 C# using System; // Structure for a node public class Node {  public int data;  public Node next; } // Class for Circular Linked List public class CircularLinkedList {  // Function to insert a node at the  // beginning of a Circular linked list  public static void Push(ref Node head_ref, int data)  {  // Create a new node and make head  // as next of it.  Node ptr1 = new Node();  ptr1.data = data;  ptr1.next = head_ref;  // If linked list is not NULL then  // set the next of last node  if (head_ref != null) {  // Find the node before head and  // update next of it.  Node temp = head_ref;  while (temp.next != head_ref)  temp = temp.next;  temp.next = ptr1;  }  else  // For the first node  ptr1.next = ptr1;  head_ref = ptr1;  }  // Function to print nodes in a given  // circular linked list  public static void PrintList(Node head)  {  Node temp = head;  if (head != null) {  do {  Console.Write(temp.data + ' ');  temp = temp.next;  } while (temp != head);  }  Console.WriteLine();  }  // Function to delete a given node  // from the list  public static void DeleteNode(ref Node head, int key)  {  // If linked list is empty  if (head == null)  return;  // If the list contains only a  // single node  if (head.data == key && head.next == head) {  head = null;  return;  }  Node last = head, d;  // If head is to be deleted  if (head.data == key) {  // Find the last node of the list  while (last.next != head)  last = last.next;  // Point last node to the next of  // head i.e. the second node  // of the list  last.next = head.next;  head = last.next;  return;  }  // Either the node to be deleted is  // not found or the end of list  // is not reached  while (last.next != head && last.next.data != key) {  last = last.next;  }  // If node to be deleted was found  if (last.next.data == key) {  d = last.next;  last.next = d.next;  }  else  Console.WriteLine(  'Given node is not found in the list!!!');  }  // Driver code  public static void Main()  {  // Initialize lists as empty  Node head = null;  // Created linked list will be  // 2->5->7->8->10 Push(atsauces galva, 2);  Push(atsauces galva, 5);  Push(atsauces galva, 7);  Push(atsauces galva, 8);  Push(atsauces galva, 10);  Console.Write('Saraksts pirms dzēšanas: ');  Drukas saraksts(galva);  DeleteNode(ref head, 7);  Console.Write('Saraksts pēc dzēšanas: ');  Drukas saraksts(galva);  } }>
 Javascript  // Javascript program to delete a given key from linked list.  // Structure for a node  class Node {  constructor() {  this.data;  this.next;  }  }  // Function to insert a node at the  // beginning of a Circular linked list  function push(head, data) {  // Create a new node and make head  // as next of it.  var ptr1 = new Node();  ptr1.data = data;  ptr1.next = head;  // If linked list is not NULL then  // set the next of last node  if (head != null) {  // Find the node before head and  // update next of it.  let temp = head;  while (temp.next != head) temp = temp.next;  temp.next = ptr1;  }  // For the first node  else ptr1.next = ptr1;  head = ptr1;  return head;  }  // Function to print nodes in a given  // circular linked list  function printList(head) {  let tempp = head;  if (head != null) {  do {  console.log(tempp.data);  tempp = tempp.next;  } while (tempp != head);  }  }  // Function to delete a given node  // from the list  function deleteNode(head, key) {  // If linked list is empty  if (head == null) return;  // If the list contains only a  // single node  if (head.data == key && head.next == head) {  head = null;  return;  }  let last = head;  // If head is to be deleted  if (head.data == key) {  // Find the last node of the list  while (last.next != head) last = last.next;  // Point last node to the next of  // head i.e. the second node  // of the list  last.next = head.next;  head = last.next;  return;  }  // Either the node to be deleted is  // not found or the end of list  // is not reached  while (last.next != head && last.next.data != key) {  last = last.next;  }  // If node to be deleted was found  if (last.next.data == key) {  d = last.next;  last.next = d.next;  d = null;  } else console.log('Given node is not found in the list!!!');  }  // Driver code  // Initialize lists as empty  head = null;  // Created linked list will be  // 2->5->7->8->10 galva = push(head, 2);  galva = push(galva, 5);  galva = push(galva, 7);  galva = push(galva, 8);  galva = push(galva, 10);  console.log('Saraksts pirms dzēšanas: ');  drukas saraksts(galva);  dzēstNode(galva, 7);  console.log('Saraksts pēc dzēšanas: ');  drukas saraksts(galva);>>Python35->7->8->10 galva = push (galva, 2) galva = push (galva, 5) galva = push (galva, 7) galva = push (galva, 8) galva = push (galva, 10) print('Saraksts pirms dzēšanas: ') printList(head) deleteNode(head, 7) print('List After Deletion: ') printList(head)>
   
  Izvade  List Before Deletion: 10 8 7 5 2 List After Deletion: 10 8 5 2>
     Laika sarežģītība:    O(N), Sliktākais gadījums notiek, ja dzēšamais elements ir pēdējais elements un mums ir jāpārvietojas pa visu sarakstu.  
    Palīgtelpa:    O(1), kā pastāvīga papildu telpa tiek izmantota.
     Apļveida saistīto sarakstu priekšrocības:     
Jebkurš mezgls var būt sākumpunkts. Mēs varam šķērsot visu sarakstu, sākot no jebkura punkta. Mums vienkārši jāapstājas, kad pirmais apmeklētais mezgls tiek apmeklēts vēlreiz.
Noder rindas ieviešanai. Atšķirībā no šis ieviešanu, mums nav jāuztur divas norādes priekšpusē un aizmugurē, ja izmantojam apļveida saistīto sarakstu. Mēs varam saglabāt rādītāju uz pēdējo ievietoto mezglu, un priekšpusi vienmēr var iegūt kā nākamo pēc pēdējā.
Apļveida saraksti ir noderīgi lietojumprogrammās, lai atkārtoti apbrauktu sarakstu. Piemēram, ja datorā darbojas vairākas lietojumprogrammas, parasti operētājsistēma ievieto esošās lietojumprogrammas sarakstā un pēc tam tās pārlasa, dodot katrai no tām zināmu laiku izpildei un liekot tām gaidīt, kamēr CPU tiek piešķirts citai lietojumprogrammai. Operētājsistēmai ir ērti izmantot apļveida sarakstu, lai, sasniedzot saraksta beigas, tā varētu pārvietoties uz saraksta priekšpusi.
Apļveida divkārši saistītie saraksti tiek izmantoti, lai ieviestu uzlabotas datu struktūras, piemēram,  Fibonači kaudze  .
Apļveida saistītā saraksta ieviešana var būt salīdzinoši vienkārša, salīdzinot ar citām sarežģītākām datu struktūrām, piemēram, kokiem vai grafikiem.
Apļveida saistītā saraksta trūkumi:
Salīdzinot ar atsevišķi saistītiem sarakstiem, apļveida saraksti ir sarežģītāki.
Apļveida saraksta apgriešana ir sarežģītāka nekā viena vai divkārša apļveida saraksta apgriešana.
Ja kods netiek apstrādāts uzmanīgi, kods var nonākt bezgalīgā cilpā.
Ir grūtāk atrast saraksta beigas un kontrolēt cilpu.
Lai gan cirkulāri saistītie saraksti var būt efektīvi noteiktās lietojumprogrammās, to veiktspēja noteiktos gadījumos var būt lēnāka nekā citām datu struktūrām, piemēram, ja saraksts ir jākārto vai jāmeklē.
Apļveida saistītie saraksti nenodrošina tiešu piekļuvi atsevišķiem mezgliem
Apļveida saistīto sarakstu lietojumi:
Vairāku spēlētāju spēlēs tas tiek izmantots, lai katram spēlētājam dotu iespēju spēlēt.
Apļveida saistīto sarakstu var izmantot, lai sakārtotu vairākas operētājsistēmas darbojošās lietojumprogrammas. Šīs lietojumprogrammas atkārto OS.
Apļveida saistītos sarakstus var izmantot resursu piešķiršanas problēmās.
Cirkulāri saistītie saraksti parasti tiek izmantoti, lai ieviestu apļveida buferus,
Apļveida saistītos sarakstus var izmantot simulācijās un spēlēs.
Kāpēc cirkulārs saistīts saraksts?
Mezgls vienmēr norāda uz citu mezglu, tāpēc NULL piešķiršana nav nepieciešama.
Kā sākumpunktu var iestatīt jebkuru mezglu.
Mezgli tiek ātri šķērsoti no pirmā līdz pēdējam.
    Nākamās ziņas:        Circular Linked List | 2. komplekts (šķērsošana)           Apļveida atsevišķi saistītais saraksts | Ievietošana     Lūdzu, rakstiet komentārus, ja atrodat kļūdu iepriekš minētajā kodā/algoritmā vai atrodiet citus veidus, kā atrisināt to pašu problēmu

TechCodeview

Kas ir Circular saistītais saraksts?

Apļveida saistītā saraksta attēlojums:

Darbības apļveida saistītajā sarakstā:

1. Ievietošana apļveida saistītajā sarakstā:

2. Dzēšana apļveida saistītā sarakstā:

Apļveida saistīto sarakstu priekšrocības:

Apļveida saistītā saraksta trūkumi:

Apļveida saistīto sarakstu lietojumi:

Kāpēc cirkulārs saistīts saraksts?