Binārais meklēšanas koks ir datu struktūra, ko izmanto datorzinātnēs, lai sakārtotu un uzglabātu datus. Binārās meklēšanas koks seko visām binārā koka un tā īpašībām pa kreisi bērns satur vērtības, kas ir mazākas par vecāku mezglu un pa labi bērns satur vērtības, kas ir lielākas par vecāku mezglu. Šī hierarhiskā struktūra ļauj efektīvi Meklēšana , Ievietošana , un Dzēšana operācijas ar kokā saglabātajiem datiem.

Binārais meklēšanas koks

Satura rādītājs

• Kas ir binārās meklēšanas koks?
• Binārā meklēšanas koka īpašības
• Vērtību dublikātu apstrāde binārajā meklēšanas kokā
• Operācijas, kas veiktas ar BST
• 1. Meklējiet mezglu BST
• 2. Ievietojiet mezglu BST
• 3. Dzēsiet BST mezglu
• 4. Traversal (BST šķērsošana kārtībā)
• BST lietojumprogrammas
• Priekšrocības
• Trūkumi
• FAQ (bieži uzdotie jautājumi) par bināro meklēšanas koku:

Kas ir binārās meklēšanas koks?

Binārais meklēšanas koks (BST) ir īpašs veids binārais koks kurā mezgla kreisā bērnā vērtība ir mazāka par mezgla vērtību un labā bērna vērtība ir lielāka par mezgla vērtību. Šo rekvizītu sauc par BST rekvizītu, un tas ļauj efektīvi meklēt, ievietot un dzēst elementus kokā.

Binārās meklēšanas koka īpašības:

• Mezgla kreisajā apakškokā ir tikai mezgli, kuru atslēgas ir mazākas par mezgla atslēgu.
• Mezgla labajā apakškokā ir tikai mezgli, kuru atslēgas ir lielākas par mezgla atslēgu.
• Tas nozīmē, ka viss, kas atrodas pa kreisi no saknes, ir mazāks par saknes vērtību un viss, kas atrodas pa labi no saknes, ir lielāks par saknes vērtību. Pateicoties šai darbībai, binārā meklēšana ir ļoti vienkārša.
• Kreisajam un labajam apakškokam ir jābūt arī bināram meklēšanas kokam.
• Nedrīkst būt mezglu dublikātu (BST var būt dublētas vērtības ar dažādām apstrādes metodēm)

Vērtību dublikātu apstrāde binārajā meklēšanas kokā:

• Mums ir jāievēro konsekvents process, t.i., dublikāta vērtība jāsaglabā kreisajā pusē vai dublikāta vērtība saknes labajā pusē, taču jāievēro jūsu pieeja.

Pamatoperācijas binārajā meklēšanas kokā:

1. Meklējiet mezglu BST:

Meklēšana BST nozīmē noteikta mezgla atrašanu datu struktūrā. Binārajā meklēšanas kokā mezgla meklēšana ir vienkārša, jo tam ir noteikta secība. Mezgla meklēšanas darbības binārās meklēšanas kokā ir norādītas šādi:

kā iegūt Apple emocijzīmes operētājsistēmā Android

1. Vispirms salīdziniet meklējamo elementu ar koka saknes elementu.
   • Ja sakne ir saskaņota ar mērķa elementu, atgrieziet mezgla atrašanās vietu.
   • Ja tas nav saskaņots, pārbaudiet, vai vienums ir mazāks par saknes elementu, ja tas ir mazāks par saknes elementu, tad pārejiet uz kreiso apakškoku.
   • Ja tas ir lielāks par saknes elementu, pārejiet uz labo apakškoku.
2. Atkārtojiet iepriekš minēto procedūru rekursīvi, līdz tiek atrasta atbilstība.
3. Ja elements nav atrasts vai nav kokā, atgrieziet NULL.

Tagad sapratīsim meklēšanu binārajā kokā, izmantojot piemēru:

Tālāk ir norādīts BST, un mums ir jāmeklē 6. elements.

Kods:

Tālāk ir norādīta meklēšanas ieviešana BST:

// C++ function to search a given key in a given BST #include  using namespace std; struct node {  int key;  struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) {  struct node* temp  = new struct node;  temp->atslēga = prece;  temp->pa kreisi = temp->pa labi = NULL;  atgriešanās temperatūra; } // Lietderības funkcija, lai ievietotu // jaunu mezglu ar doto atslēgu BST struct node* insert(struct node* node, int key) { // Ja koks ir tukšs, atgriež jaunu mezglu if (node ​​== NULL ) return newNode(key);  // Pretējā gadījumā atkārtojiet lejup pa koku if (atslēga< node->atslēga) mezgls->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);  else if (atslēga> mezgls->atslēga) node->right = insert(mezgls->labais, atslēga);  // Atgriezt (nemainītā) mezgla rādītāja atgriešanas mezglu; } // Lietderības funkcija atslēgas meklēšanai BST struct node* search(struct node* root, int key) root->key == key) return root;  // Atslēga ir lielāka par saknes atslēgu if (root->key< key)  return search(root->pa labi, atslēga);  // Atslēga ir mazāka par root's key return search(root->left, key);>>C 
// Java program to search a given key in a given BST class Node {  int key;  Node left, right;  public Node(int item) {  key = item;  left = right = null;  } } class BinarySearchTree {  Node root;  // Constructor  BinarySearchTree() {  root = null;  }  // A utility function to insert  // a new node with given key in BST  Node insert(Node node, int key) {  // If the tree is empty, return a new node  if (node == null) {  node = new Node(key);  return node;  }  // Otherwise, recur down the tree  if (key < node.key)  node.left = insert(node.left, key);  else if (key>mezgls.atslēga) node.right = insert(mezgls.labais, atslēga);  // Atgriezt (nemainītā) mezgla rādītāja atgriešanas mezglu;  } // Lietderības funkcija atslēgas meklēšanai BST mezgla meklēšanā (mezgla sakne, int atslēga) // Pamata gadījumi: sakne ir null vai atslēga atrodas saknē if (root == null>
 Python 
# Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Atgriezt (nemainītu) mezgla rādītāja atgriešanas mezglu # Utilīta funkcija, lai meklētu atslēgu BST def meklēšanā (sakne, atslēga): # Pamata gadījumi: sakne ir Nulle vai atslēga atrodas saknē, ja sakne ir None vai root.key == atslēga: return root # Atslēga ir lielāka par saknes atslēgu, ja root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
 JavaScript 
// Javascript function to search a given key in a given BST class Node { constructor(key) {  this.key = key;  this.left = null;  this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) {  return new Node(key); } // Otherwise, recur down the tree if (key < node.key) {  node.left = insert(node.left, key); } else if (key>mezgls.atslēga) { mezgls.labais = ievietot(mezgls.labais, atslēga); } // Atgriezt (nemainītā) mezgla rādītāja atgriešanas mezglu; } // Lietderības funkcija atslēgas meklēšanai BST funkcijā search(root, key) { // Pamata gadījumi: sakne ir null vai atslēga atrodas saknē if (root === null || root.key === taustiņš ) { atgriezt sakni; } // Atslēga ir lielāka par saknes atslēgu if (root.key< key) {  return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
  
  
 
    2.         Ievietojiet mezglu BST         :     
Lapā vienmēr tiek ievietota jauna atslēga. Sāciet meklēt atslēgu no saknes līdz lapas mezglam. Kad lapas mezgls ir atrasts, jaunais mezgls tiek pievienots kā lapas mezgla bērns.
 
  
 
    Kods:    
 
Tālāk ir parādīta viena mezgla ievietošanas ieviešana binārajā meklēšanas kokā:
C++ 
// Given Node Structure struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp = (struct node*)malloc(  sizeof(struct node));  temp->atslēga = prece;  temp->pa kreisi = temp->pa labi = NULL;  atgriešanās temperatūra; } // Funkcija jauna mezgla ievietošanai ar // doto atslēgu BST struct node* insert(struct node* node, int key) { // Ja koks ir tukšs, atgriež jaunu mezglu if (node ​​== NULL) return newNode(atslēga);  // Pretējā gadījumā atkārtojiet lejup pa koku if (atslēga< node->atslēga) { mezgls->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);  } else if (atslēga> mezgls->atslēga) { mezgls->pa labi = ievietot(mezgls->labais, atslēga);  } // Return the node pointer return node; }>
 C 
// Given Node Structure struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->atslēga = prece;  temp->pa kreisi = temp->pa labi = NULL;  atgriešanās temperatūra; } // Funkcija jauna mezgla ievietošanai ar // doto atslēgu BST struct node* insert(struct node* node, int key) { // Ja koks ir tukšs, atgriež jaunu mezglu if (node ​​== NULL) return newNode(atslēga);  // Pretējā gadījumā atkārtojiet lejup pa koku if (atslēga< node->atslēga) { mezgls->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);  } else if (atslēga> mezgls->atslēga) { mezgls->pa labi = ievietot(mezgls->labais, atslēga);  } // Return the node pointer return node; }>
 Java 
class GFG {  // Given Node Structure  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>mezgls.atslēga) { mezgls.labais = ievietot(mezgls.labais, atslēga);  } // Return the node return node;  } }>
 Python3 
# Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Atgriezt mezgla rādītāju return node>
 Javascript 
// Given Node Structure class Node {  constructor(key){  this.key = key;  this.left = null;  this.right = null;  } } // Function to insert a new node with // given key in BST function insert(node, key) {    // If the tree is empty, return a new node  if (node == null)  return new Node(key);  // Otherwise, recur down the tree  if (key < node.key)  {  node.left = insert(node.left, key);  }  else if (key>mezgls.atslēga) { mezgls.labais = ievietot(mezgls.labais, atslēga);  } // Return the node pointer return node; }>
  
    Laika sarežģītība:    O(N), kur N ir BST mezglu skaits  
    Palīgtelpa:    O(1)
 
    3.          Dzēst BST mezglu     :
To izmanto, lai no BST dzēstu mezglu ar noteiktu atslēgu un atgrieztu jauno BST.
 
Dažādi mezgla dzēšanas scenāriji:
 
    Dzēšams mezgls ir lapas mezgls       :    
Tas ir vienkārši, jūs varat to vienkārši atcelt.
kas ir darbvirsmas ini
  
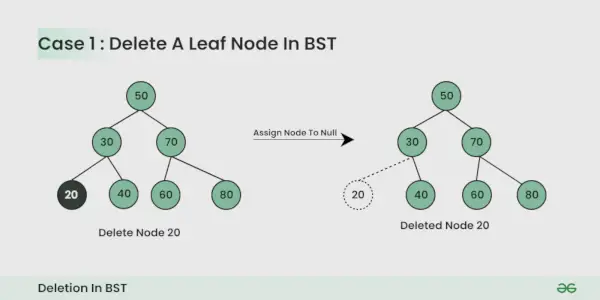
    Dzēšamajam mezglam ir viens bērns       :     
Jūs varat vienkārši aizstāt mezglu ar bērnu mezglu.
  
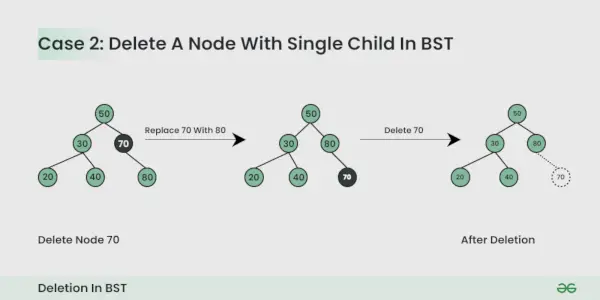
    Dzēšamajam mezglam ir divi bērni       :     
Šeit mums tas ir jādara    mezgla dzēšana ir tāda, ka iegūtais koks atbilst BST īpašībām.    Viltība ir atrast mezgla nepareizo pēcteci. Kopējiet secības pēcteces saturu uz mezglu un izdzēsiet kārtas pēcteci.
  
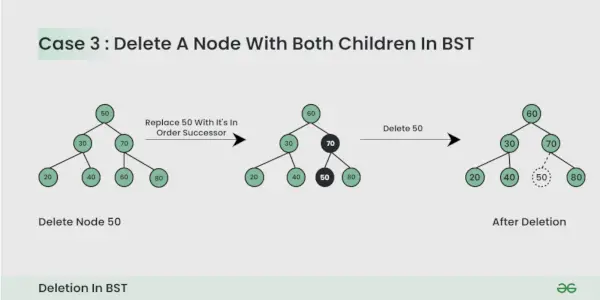
Dzēšot BST mezglu, ievērojiet šādas lietas:
 
Jāizdomā, kāda būs dzēšamā mezgla aizstāšana.
Vēlaties minimālus traucējumus esošajai koka struktūrai
Var ņemt nomaiņas mezglu no dzēstajiem mezgliem pa kreisi vai pa labi.
Ja ņemam no kreisā apakškoka, mums ir jāņem lielākā vērtība kreisajā apakškokā.
Ja ņemam no labā apakškoka, mums ir jāņem mazākā vērtība labajā apakškokā.
    Kods:    
 
Tālāk ir norādīta dzēšanas ieviešana BST:
C++ 
// C++ program to delete // a node of BST // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->atslēga = prece;  temp->pa kreisi = temp->pa labi = NULL;  atgriešanās temperatūra; } // Funkcija jauna mezgla ievietošanai ar // doto atslēgu BST struct node* insert(struct node* node, int key) { // Ja koks ir tukšs, atgriež jaunu mezglu if (node ​​== NULL) return newNode(atslēga);  // Pretējā gadījumā atkārtojiet lejup pa koku if (atslēga< node->atslēga) { mezgls->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);  } else if (atslēga> mezgls->atslēga) { mezgls->pa labi = ievietot(mezgls->labais, atslēga);  } // Return the node pointer return node; } // Funkcija, kas atgriež mezglu ar minimālo // šajā kokā atrasto atslēgas vērtību struct node* minValueNode(struct node* node) { struct node* current = node;  // Cilpu uz leju, lai atrastu vistālāk kreiso lapu, kamēr (pašreizējais && strāva->kreisais != NULL) pašreizējais = pašreizējais->kreisais;  atgriešanās strāva; } // Funkcija, kas dzēš atslēgu un // atgriež jauno saknes struct node* deleteNode(struct node* root, int key) { // base Case if (root == NULL) return root;  // Ja dzēšamā atslēga ir // mazāka par saknes atslēgu, // tad tā atrodas kreisajā apakškokā if (taustiņa< root->taustiņš) { sakne->pa kreisi = deleteNode(root->left, key);  } // Ja dzēšamā atslēga ir // lielāka par saknes atslēgu, // tad tā atrodas labajā apakškokā else if (key> root->key) { root->right = deleteNode(root-> pa labi, atslēga);  } // Ja atslēga ir tāda pati kā root's atslēga, // tad šis ir mezgls //, kas jādzēš. Cits { // Mezgls tikai ar vienu bērnu // vai bez bērna, ja (root->left == NULL) { struct node* temp = root->right;  brīvs(sakne);  atgriešanās temperatūra;  } else if (root->right == NULL) { struct node* temp = root->left;  brīvs(sakne);  atgriešanās temperatūra;  } // Mezgls ar diviem bērniem: // Iegūstiet kārtas pēcteci (mazākais // labajā apakškokā) struct node* temp = minValueNode(root->right);  // Kopēt secības pārņēmēja // saturu šajā mezglā root->key = temp->key;  // Dzēst secības pēcteci root->right = deleteNode(root->right, temp->key);  } atgriezties sakne; }>
 C 
// C program to delete // a node of BST // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->atslēga = prece;  temp->pa kreisi = temp->pa labi = NULL;  atgriešanās temperatūra; } // Funkcija jauna mezgla ievietošanai ar // doto atslēgu BST struct node* insert(struct node* node, int key) { // Ja koks ir tukšs, atgriež jaunu mezglu if (node ​​== NULL) return newNode(atslēga);  // Pretējā gadījumā atkārtojiet lejup pa koku if (atslēga< node->atslēga) { mezgls->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);  } else if (atslēga> mezgls->atslēga) { mezgls->pa labi = ievietot(mezgls->labais, atslēga);  } // Return the node pointer return node; } // Funkcija, kas atgriež mezglu ar minimālo // šajā kokā atrasto atslēgas vērtību struct node* minValueNode(struct node* node) { struct node* current = node;  // Cilpu uz leju, lai atrastu vistālāk kreiso lapu, kamēr (pašreizējais && strāva->kreisais != NULL) pašreizējais = pašreizējais->kreisais;  atgriešanās strāva; } // Funkcija, kas dzēš atslēgu un // atgriež jauno saknes struct node* deleteNode(struct node* root, int key) { // base Case if (root == NULL) return root;  // Ja dzēšamā atslēga ir // mazāka par saknes atslēgu, // tad tā atrodas kreisajā apakškokā if (taustiņa< root->taustiņš) { sakne->pa kreisi = deleteNode(root->left, key);  } // Ja dzēšamā atslēga ir // lielāka par saknes atslēgu, // tad tā atrodas labajā apakškokā else if (key> root->key) { root->right = deleteNode(root-> pa labi, atslēga);  } // Ja atslēga ir tāda pati kā root's atslēga, // tad šis ir mezgls //, kas jādzēš. Cits { // Mezgls tikai ar vienu bērnu // vai bez bērna, ja (root->left == NULL) { struct node* temp = root->right;  brīvs(sakne);  atgriešanās temperatūra;  } else if (root->right == NULL) { struct node* temp = root->left;  brīvs(sakne);  atgriešanās temperatūra;  } // Mezgls ar diviem bērniem: // Iegūstiet kārtas pēcteci (mazākais // labajā apakškokā) struct node* temp = minValueNode(root->right);  // Kopēt secības pārņēmēja // saturu šajā mezglā root->key = temp->key;  // Dzēst secības pēcteci root->right = deleteNode(root->right, temp->key);  } atgriezties sakne; }>
 Java 
// Java program for Delete a Node of BST class GFG {  // Given Node node  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>mezgls.atslēga) { mezgls.labais = ievietot(mezgls.labais, atslēga);  } // Return the node return node;  } // Funkcija, kas atgriež mezglu ar minimālo // šajā koka statiskajā mezglā atrasto atslēgas vērtību minValueNode(node ​​node) { node current = node;  // Veiciet cilpu uz leju, lai atrastu galējo kreiso lapu, kamēr (current != null && current.left != null) current = current.left;  atgriešanās strāva;  } // Funkcija, kas dzēš atslēgu un // atgriež jauno saknes statisko mezglu deleteNode(node ​​root, int key) { // base Case if (root == null) return root;  // Ja dzēšamā atslēga ir // mazāka par saknes atslēgu, // tad tā atrodas kreisajā apakškokā if (taustiņa< root.key) {  root.left = deleteNode(root.left, key);  }  // If the key to be deleted is  // greater than the root's key,  // then it lies in right subtree  else if (key>root.key) { root.right = deleteNode(root.right, key);  } // Ja atslēga ir tāda pati kā root's atslēga, // tad šis ir mezgls //, kas jāizdzēš. else { // Mezgls ar tikai vienu bērnu // vai bez bērna if (root.left == null) { mezgla temp = root.right;  atgriešanās temperatūra;  } else if (root.right == null) { node temp = root.left;  atgriešanās temperatūra;  } // Mezgls ar diviem bērniem: // Iegūstiet secības pēcteci(vismazākais // labajā apakškokā) node temp = minValueNode(root.right);  // Kopēt secības pārņēmēja // saturu šajā mezglā root.key = temp.key;  // Dzēst secības pēcteci root.right = deleteNode(root.right, temp.key);  } atgriezties sakne;  }>
 Python 
# Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Atgriezt mezgla rādītāju return root # Funkcija, lai veiktu inorder šķērsošanu BST def inorder(root): if root: inorder(root.left) print(root. taustiņš, end=' ') inorder(root.right) # Funkcija, kas atgriež mezglu ar minimālo # atslēgas vērtību, kas atrasta šajā kokā def minValueNode(node): current = node # Veiciet cilpu uz leju, lai atrastu vistālāk esošo lapu, kamēr pašreizējā un current.left nav Nav: pašreizējais = current.left return current # Funkcija, kas izdzēš atslēgu un # atgriež jauno saknes def deleteNode(root, key): # pamatreģistrs, ja sakne ir Nav: return root # Ja atslēga ir dzēstais ir # mazāks par saknes atslēgu, # tad tas atrodas kreisajā apakškokā, ja atslēga< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Ja atslēga ir tāda pati kā root's atslēga, # tad šis ir mezgls #, kas jādzēš citādi: # Mezgls tikai ar vienu bērnu # vai bez bērna ja root.left ir Nav: temp = root.right root = Nav atgriešanās temp elif root.right ir Nav: temp = root.left root = Nav atgriešanās temp # Mezgls ar diviem bērniem: # Iegūstiet secības pēcteci (mazāko # labais apakškoks) temp = minValueNode(root.right) # Kopējiet secības pēcteča # saturu šajā mezglā root.key = temp.key # Dzēst kārtas pēcteci root.right = deleteNode(root.right, temp.key) atgriezt sakni>> 
    4.         Šķērsošana (BST secīga šķērsošana)         :    
Bināro meklēšanas koku (BST) gadījumā Inorder traversal dod mezglus nesamazināmā secībā. Vispirms apmeklējam kreiso bērnu, tad sakni un tad labo bērnu.
regexp_like mysql
 
Tālāk ir aprakstīts, kā veikt binārās meklēšanas koka šķērsošanu:
C++atslēga;  inorder(sakne->pa labi);  } } // Draivera kods int main() { /* Izveidosim šādu BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // BST saknes izveide = insert(root, 50);  ievietot(sakne, 30);  ievietot(sakne, 20);  ievietot(sakne, 40);  ievietot(sakne, 70);  ievietot(sakne, 60);  ievietot(sakne, 80);  // Funkcija Call inorder(root);  atgriezties 0; } // Šo kodu ir sagatavojis shivanisinghss2110>
 C 
// C program to implement // inorder traversal of BST #include  #include  // Given Node node struct node {  int key;  struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) {  struct node* temp  = (struct node*)malloc(  sizeof(struct node));  temp->atslēga = prece;  temp->pa kreisi = temp->pa labi = NULL;  atgriešanās temperatūra; } // Funkcija jauna mezgla ievietošanai ar // doto atslēgu BST struct node* insert(struct node* node, int key) { // Ja koks ir tukšs, atgriež jaunu mezglu if (node ​​== NULL) return newNode(atslēga);  // Pretējā gadījumā atkārtojiet lejup pa koku if (atslēga< node->atslēga) { mezgls->pa kreisi = ievietot(mezgls->pa kreisi, atslēga);  } else if (atslēga> mezgls->atslēga) { mezgls->pa labi = ievietot(mezgls->labais, atslēga);  } // Return the node pointer return node; } // Funkcija BST inorder traversal veikšanai void inorder(struct node* root) { if (root != NULL) { inorder(root->left);  printf('%d ', root->key);  inorder(sakne->pa labi);  } } // Draivera kods int main() { /* Izveidosim šādu BST 50 /  30 70 /  /  20 40 60 80 */ struct node* root = NULL;  // BST saknes izveide = insert(root, 50);  ievietot(sakne, 30);  ievietot(sakne, 20);  ievietot(sakne, 40);  ievietot(sakne, 70);  ievietot(sakne, 60);  ievietot(sakne, 80);  // Funkcija Call inorder(root);  atgriezties 0; }>
 Java 
import java.io.*; // Java program for Inorder Traversal class GFG {  // Given Node node  static class node {  int key;  node left, right;  };  // Function to create a new BST node  static node newNode(int item)  {  node temp = new node();  temp.key = item;  temp.left = temp.right = null;  return temp;  }  // Function to insert a new node with  // given key in BST  static node insert(node node, int key)  {  // If the tree is empty, return a new node  if (node == null)  return newNode(key);  // Otherwise, recur down the tree  if (key < node.key) {  node.left = insert(node.left, key);  }  else if (key>mezgls.atslēga) { mezgls.labais = ievietot(mezgls.labais, atslēga);  } // Return the node return node;  } // Funkcija BST inorder šķērsošanai static void inorder(mezgla sakne) { if (root != null) { inorder(root.left);  System.out.print(' ' + root.key);  inorder(root.right);  } } // Draivera kods public static void main(String[] args) { /* Izveidosim šādu BST 50 /  30 70 /  /  20 40 60 80 */ node root = null;  // ievietojot vērtību 50 sakne = insert(root, 50);  // ievietojot vērtību 30 insert(root, 30);  // ievietojot vērtību 20 insert(root, 20);  // ievietojot vērtību 40 insert(root, 40);  // ievietojot vērtību 70 insert(root, 70);  // ievietojot vērtību 60 insert(root, 60);  // ievietojot vērtību 80 insert(root, 80);  // izdrukāt BST inorder(root);  } } // Šo kodu ir sagatavojis abhijitjadhav1998>
 Python3 
# Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Atgriezt mezgla rādītāju return node # Funkcija, lai veiktu inorder šķērsošanu BST def inorder(root): if root: inorder(root.left) print(root. taustiņš, end=' ') inorder(root.right) # Draivera kods if __name__ == '__main__': # Izveidosim šādu BST # 50 # /  # 30 70 # /  /  # 20 40 60 80 sakne = None # BST saknes izveide = insert(root, 50) insert(root, 30) insert(root, 20) insert(root, 40) insert(root, 70) insert(root, 60) insert(root , 80) # Funkcija Call inorder(root) #Šo kodu sniedz japmeet01>
   
  Izvade  
 20 30 40 50 60 70 80>
 
    Laika sarežģītība:    O(N), kur N ir BST mezglu skaits  
    Palīgtelpa:    O(1)
 
    BST pielietojumi:    
    Grafiku algoritmi:    BST var izmantot, lai ieviestu grafiku algoritmus, piemēram, minimālo aptverošo koku algoritmos.
    Prioritārās rindas:    BST var izmantot prioritāro rindu ieviešanai, kur elements ar augstāko prioritāti atrodas koka saknē, bet elementi ar zemāku prioritāti tiek glabāti apakškokos.
    Pašbalansējošais binārais meklēšanas koks:    BST var izmantot kā pašbalansējošas datu struktūras, piemēram, AVL koks un sarkanmelnais koks.
    Datu glabāšana un izguve:    BST var izmantot, lai ātri uzglabātu un izgūtu datus, piemēram, datu bāzēs, kur konkrēta ieraksta meklēšanu var veikt logaritmiskā laikā.
    Priekšrocības:    
    Ātrā meklēšana:    Konkrētas vērtības meklēšanai BST ir vidējā laika sarežģītība O(log n), kur n ir mezglu skaits kokā. Tas ir daudz ātrāk nekā elementa meklēšana masīvā vai saistītajā sarakstā, kura laika sarežģītība sliktākajā gadījumā ir O(n).
    Pasūtījuma šķērsošana:    BST var šķērsot secībā, kas apmeklē kreiso apakškoku, sakni un labo apakškoku. To var izmantot datu kopas kārtošanai.
    Kosmosa efektīva:    BST ir vietas ziņā efektīvi, jo atšķirībā no masīviem un saistītajiem sarakstiem tie nesaglabā lieku informāciju.
    Trūkumi:    
    Šķībi koki:    Ja koks kļūst šķībs, meklēšanas, ievietošanas un dzēšanas operāciju laika sarežģītība būs O(n), nevis O(log n), kas var padarīt koku neefektīvu.
    Nepieciešams papildu laiks:    Pašbalansējošiem kokiem ir nepieciešams papildu laiks, lai saglabātu līdzsvaru ievietošanas un dzēšanas laikā.
    Efektivitāte:    BST nav efektīvas datu kopām ar daudziem dublikātiem, jo ​​tie tērēs vietu.
FAQ(Bieži uzdotie jautājumi)binārajā meklēšanas kokā:
    1. Kas ir binārais meklēšanas koks?    
 
Binārais meklēšanas koks (BST) ir    binārs koks, kurā katrs kreisā apakškoka mezgls ir mazāks par sakni un katrs labā apakškoka mezgls ir ar vērtību, kas ir lielāka par sakni    . Binārā meklēšanas koka īpašības ir rekursīvas: ja mēs uzskatām jebkuru mezglu par sakni, šīs īpašības paliks patiesas.
 
2. Kas ir binārā meklēšanas koka operācija?
 
Binārajā meklēšanas kokā ir trīs galvenās darbības:    1. Ievietošana, 2. Dzēšana, 3. Meklēšana.    Tā īpašību dēļ tā ir efektīva, lai meklētu jebkuru elementu binārajā meklēšanas kokā.
 
3. Kas ir binārās meklēšanas koks un AVL koks?
 
    Binārais meklēšanas koks       :    Binārais meklēšanas koks (BST) ir binārs koks, kurā katrs kreisā apakškoka mezgls ir mazāks par sakni un katrs labā apakškoka mezgls ir ar vērtību, kas ir lielāka par sakni.
 
    AVL koks       :    Binārie meklēšanas koki (BST), kas paši līdzsvaro un rotē automātiski, ir zināmi kā AVL koki.
 
4. Kādas ir binārās meklēšanas koka izmantošanas iespējas?
 
Bināros meklēšanas kokus var izmantot, lai ieviestu abstraktus datu tipus, piemēram,    dinamiskās kopas, uzmeklēšanas tabulas un prioritārās rindas,    un izmantots    šķirošanas algoritmi    piemēram, koku šķirošana.
 
5. Kāda ir atšķirība starp bināro meklēšanas koku un bināro koku?
 
Binārais meklēšanas koks ir koks, kas seko noteiktai secībai, lai sakārtotu elementus, turpretim binārais koks neseko nevienai secībai.
 
    Saistītie raksti:    
 
     BST pielietošana     
     Binārās meklēšanas koka lietojumprogrammas, priekšrocības un trūkumi     
     Ievietošana binārajā meklēšanas kokā (BST)     
     Meklēšana binārajā meklēšanas kokā (BST)     
     Dzēšana binārajā meklēšanas kokā (BST)