The Floida-Voršala algoritms , kas nosaukts tā veidotāju vārdā Roberts Floids un Stīvens Voršals , ir fundamentāls algoritms datorzinātnēs un grafu teorijā. To izmanto, lai atrastu īsākos ceļus starp visiem mezglu pāriem svērtā grafikā. Šis algoritms ir ļoti efektīvs un var apstrādāt grafikus ar abiem pozitīvs un n egatīvie malu svari , padarot to par daudzpusīgu rīku dažādu tīkla un savienojamības problēmu risināšanai.
Satura rādītājs
- Floida Voršala algoritms
- Ideja aiz Floida Voršala algoritma
- Floida Voršala algoritma algoritms
- Floida Voršala algoritma pseidokods
- Floida Voršala algoritma ilustrācija
- Floida Voršala algoritma sarežģītības analīze
- Kāpēc Floyd-Warshall algoritms ir labāks blīviem grafikiem, nevis retajiem grafikiem?
- Svarīgi intervijas jautājumi saistībā ar Floyd-Warshall
- Floida-Voršala algoritma reālās pasaules pielietojumi
Floida Voršala algoritms:
The Floida Voršala algoritms ir visu pāru īsākā ceļa algoritms atšķirībā no Dijkstra un Belmens Fords kas ir viena avota īsākā ceļa algoritmi. Šis algoritms darbojas gan režisēts un nevirzīts svērts grafiki. Taču tas nedarbojas grafikiem ar negatīviem cikliem (kurā cikla šķautņu summa ir negatīva). Tas seko Dinamiskā programmēšana pieeja, lai pārbaudītu visus iespējamos ceļus, kas iet caur katru iespējamo mezglu, lai aprēķinātu īsāko attālumu starp katru mezglu pāri.
atlasīt kā
Ideja aiz Floida Voršala algoritma:
Pieņemsim, ka mums ir grafiks G[][] ar IN virsotnes no 1 uz N . Tagad mums ir jānovērtē a shortestPathMatrix[][] kur ir hortestPathMatrix[i][j] apzīmē īsāko ceļu starp virsotnēm i un j .
Acīmredzot īsākais ceļš starp i uz j būs daži k starpmezglu skaits. Floyd Warshall algoritma ideja ir apstrādāt katru virsotni no 1 uz N kā starpmezgls pa vienam.
Nākamajā attēlā parādīta iepriekš minētā optimālā apakšstruktūras īpašība floyd Warshall algoritmā:
Floida Voršala algoritma algoritms:
- Vispirms inicializējiet risinājuma matricu tāpat kā ievades grafika matricu.
- Pēc tam atjauniniet risinājuma matricu, visas virsotnes uzskatot par starpvirsotni.
- Ideja ir izvēlēties visas virsotnes pa vienai un atjaunināt visus īsākos ceļus, kas ietver izvēlēto virsotni kā starppunktu īsākajā ceļā.
- Kad mēs izvēlamies virsotnes numuru k kā starpvirsotne mēs jau esam apsvēruši virsotnes {0, 1, 2, .. k-1} kā starpvirsotnes.
- Katram pārim (i, j) avota un galamērķa virsotnēm, ir divi iespējamie gadījumi.
- k nav starpvirsotne īsākā ceļā no i uz j . Mēs saglabājam vērtību dist[i][j] tā kā tas ir.
- k ir starpvirsotne īsākā ceļā no i uz j . Mēs atjauninām vērtību dist[i][j] kā dist[i][k] + dist[k][j], ja dist[i][j]> dist[i][k] + dist[k][j]
Floida Voršala algoritma pseidokods:>
Ja k = 0 līdz n - 1
Ja i = 0 līdz n - 1
Ja j = 0 līdz n – 1
Attālums[i, j] = min(attālums[i, j], attālums[i, k] + attālums[k, j])stacks javakur i = avota mezgls, j = galamērķa mezgls, k = starpmezgls
Floida Voršala algoritma ilustrācija:
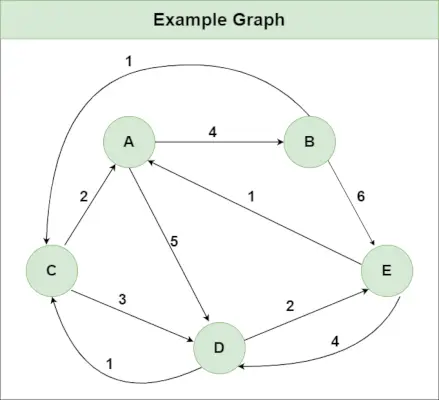
Ieteicamā prakse Izmēģiniet to!Pieņemsim, ka mums ir grafiks, kā parādīts attēlā:
1. darbība : Inicializējiet Distance[][] matricu, izmantojot ievades grafiku tā, lai attālums[i][j]= malas svars no i uz j , arī Attālums[i][j] = Bezgalība, ja nav malas no i uz j.
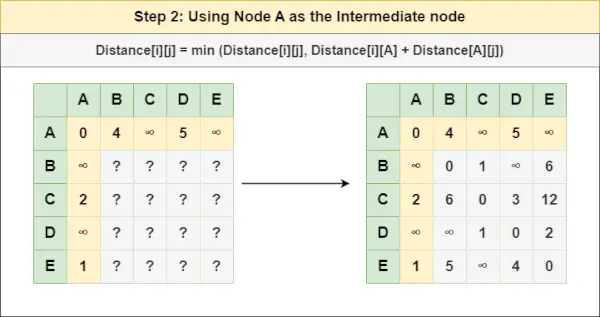
2. darbība : Apstrādājiet mezglu A kā starpmezglu un aprēķiniet attālumu[][] katram {i,j} mezglu pārim, izmantojot formulu:
= attālums[i][j] = minimālais (attālums[i][j], (attālums no i līdz A ) + (Attālums no A uz j))
= attālums[i][j] = minimālais (attālums[i][j], attālums[i][ A ] + attālums[ A ][j])3. darbība : Apstrādājiet mezglu B kā starpmezglu un aprēķiniet attālumu[][] katram {i,j} mezglu pārim, izmantojot formulu:
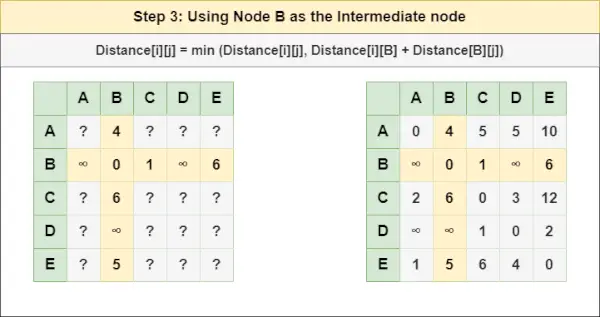
= attālums[i][j] = minimālais (attālums[i][j], (attālums no i līdz B ) + (Attālums no B uz j))
= attālums[i][j] = minimālais (attālums[i][j], attālums[i][ B ] + attālums[ B ][j])metodes ignorēšana Java4. darbība : Apstrādājiet mezglu C kā starpmezglu un aprēķiniet attālumu[][] katram {i,j} mezglu pārim, izmantojot formulu:
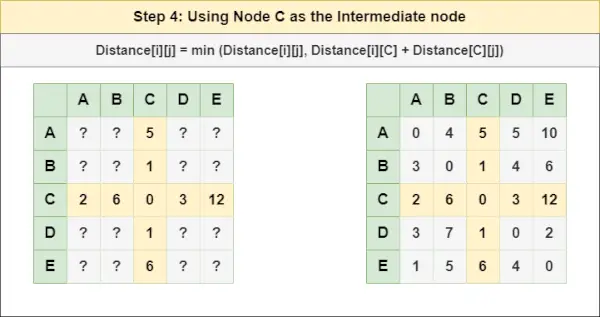
= attālums[i][j] = minimālais (attālums[i][j], (attālums no i līdz C ) + (Attālums no C uz j))
= attālums[i][j] = minimālais (attālums[i][j], attālums[i][ C ] + attālums[ C ][j])5. darbība : Apstrādājiet mezglu D kā starpmezglu un aprēķiniet attālumu[][] katram {i,j} mezglu pārim, izmantojot formulu:
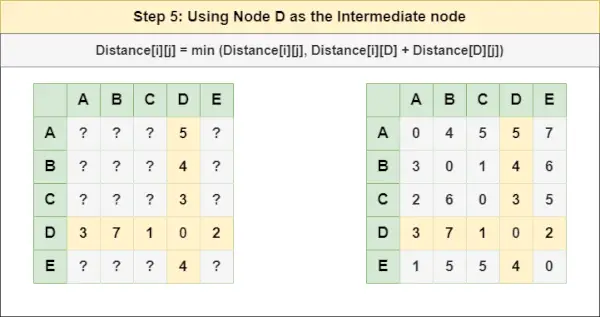
= attālums[i][j] = minimālais (attālums[i][j], (attālums no i līdz D ) + (Attālums no D uz j))
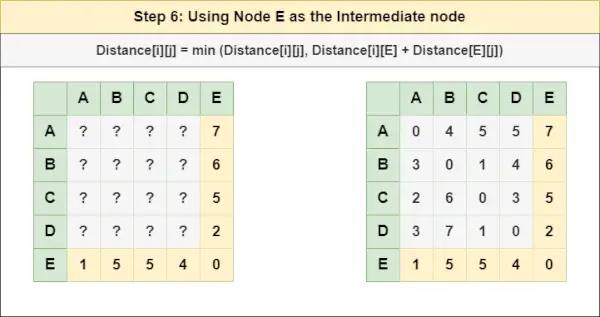
= attālums[i][j] = minimālais (attālums[i][j], attālums[i][ D ] + attālums[ D ][j])6. darbība : Apstrādājiet mezglu UN kā starpmezglu un aprēķiniet attālumu[][] katram {i,j} mezglu pārim, izmantojot formulu:
= attālums[i][j] = minimālais (attālums[i][j], (attālums no i līdz UN ) + (Attālums no UN uz j))
= attālums[i][j] = minimālais (attālums[i][j], attālums[i][ UN ] + attālums[ UN ][j])7. darbība : Tā kā visi mezgli ir uzskatīti par starpmezgliem, mēs tagad varam atgriezt atjaunināto Distance[][] matricu kā savu atbilžu matricu.
daļējs atvasinājuma simbols latekss
Tālāk ir aprakstīta iepriekš minētās pieejas īstenošana.
C++ // C++ Program for Floyd Warshall Algorithm #include using namespace std; // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value.This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Pirms iterācijas sākuma mums ir mazākie attālumi starp visiem virsotņu pāriem, lai mazākie attālumi uzskatītu tikai virsotnes kopā {0, 1, 2, .. k-1} kā starpvirsotnes. ----> Pēc iterācijas beigām virsotne Nr. k tiek pievienots starpvirtņu kopai, un kopa kļūst par {0, 1, 2, .. k} */ ja (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][j]>(dist[i][k] + dist[k][j]) && (dist[k][j] != INF && dist[i][k] != INF)) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Drukāt īsākā attāluma matricu printSolution(dist); } /* Lietderības funkcija risinājuma drukāšanai */ void printSolution(int dist[][V]) { cout<< 'The following matrix shows the shortest ' 'distances' ' between every pair of vertices
'; for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) cout << 'INF' << ' '; else cout << dist[i][j] << ' '; } cout << endl; } } // Driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int grafiks[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0} }; // Funkcijas izsaukums floydWarshall(graph); atgriezties 0; } // Šo kodu ir izstrādājis Mythri J L> C // C Program for Floyd Warshall Algorithm #include // Number of vertices in the graph #define V 4 /* Define Infinite as a large enough value. This value will be used for vertices not connected to each other */ #define INF 99999 // A function to print the solution matrix void printSolution(int dist[][V]); // Solves the all-pairs shortest path // problem using Floyd Warshall algorithm void floydWarshall(int dist[][V]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Pirms iterācijas sākuma mums ir mazākie attālumi starp visiem virsotņu pāriem, lai mazākie attālumi uzskatītu tikai virsotnes kopā {0, 1, 2, .. k-1} kā starpvirsotnes. ----> Pēc iterācijas beigām virsotne Nr. k tiek pievienots starpvirtņu kopai, un kopa kļūst par {0, 1, 2, .. k} */ ja (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path from // i to j, then update the value of // dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Print the shortest distance matrix printSolution(dist); } /* A utility function to print solution */ void printSolution(int dist[][V]) { printf( 'The following matrix shows the shortest distances' ' between every pair of vertices
'); for (int i = 0; i < V; i++) { for (int j = 0; j < V; j++) { if (dist[i][j] == INF) printf('%7s', 'INF'); else printf('%7d', dist[i][j]); } printf('
'); } } // driver's code int main() { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int grafiks[V][V] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0} }; // Funkcijas izsaukums floydWarshall(graph); atgriezties 0; }> Java // Java program for Floyd Warshall All Pairs Shortest // Path algorithm. import java.io.*; import java.lang.*; import java.util.*; class AllPairShortestPath { final static int INF = 99999, V = 4; void floydWarshall(int dist[][]) { int i, j, k; /* Add all vertices one by one to the set of intermediate vertices. --->Pirms iterācijas sākuma mums ir mazākie attālumi starp visiem virsotņu pāriem, lai mazākie attālumi uzskatītu tikai virsotnes kopā {0, 1, 2, .. k-1} kā starpvirsotnes. ----> Pēc iterācijas beigām virsotne Nr. k tiek pievienots starpvirtņu kopai, un kopa kļūst par {0, 1, 2, .. k} */ ja (k = 0; k< V; k++) { // Pick all vertices as source one by one for (i = 0; i < V; i++) { // Pick all vertices as destination for the // above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest path // from i to j, then update the value of // dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) dist[i][j] = dist[i][k] + dist[k][j]; } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int dist[][]) { System.out.println( 'The following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i][j] == INF) System.out.print('INF '); else System.out.print(dist[i][j] + ' '); } System.out.println(); } } // Driver's code public static void main(String[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int graph[][] = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0, 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = new AllPairShortestPath(); // Funkcijas izsaukums a.floydWarshall(graph); } } // Autors Aakash Hasija>>Python3Pirms iterācijas sākuma mums ir mazākie attālumi starp visiem virsotņu pāriem, lai mazākie attālumi uzskatītu tikai virsotnes no kopas {0, 1, 2, .. k-1} kā starpvirsotnes. ----> Pēc iterācijas beigām virsotne Nr. k tiek pievienots starpvirtņu kopai, un kopa kļūst par {0, 1, 2, .. k} ''' priekš k diapazonā (V): # izvēlieties visas virsotnes kā avotu pa vienai i in diapazons(V): # Izvēlieties visas virsotnes kā galamērķi # iepriekš atlasītajam avotam j diapazonā (V): # Ja virsotne k atrodas uz īsākā ceļa no # i līdz j, tad atjauniniet dist[i][ vērtību. j] dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j] ) printSolution(dist) # Lietderības funkcija risinājuma def printSolution drukāšanai (dist): print('Sekojošā matrica parāda īsākos attālumus starp katru virsotņu pāri') i diapazonā(V): j diapazonā(V): if(dist[i][j] == INF): print('%7s' % ('INF'), end=' ') else: print('%7d ' % (dist[i][j]), end=' ') if j == V-1: print() # Draivera kods if __name__ == '__main__': ''' 10 (0)------ ->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 grafiks = [[0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0 , 1], [INF, INF, INF, 0] ] # Funkciju izsaukums floydWarshall(graph) # Šo kodu sniedz Mythri J L> C# // C# program for Floyd Warshall All // Pairs Shortest Path algorithm. using System; public class AllPairShortestPath { readonly static int INF = 99999, V = 4; void floydWarshall(int[, ] graph) { int[, ] dist = new int[V, V]; int i, j, k; // Initialize the solution matrix // same as input graph matrix // Or we can say the initial // values of shortest distances // are based on shortest paths // considering no intermediate // vertex for (i = 0; i < V; i++) { for (j = 0; j < V; j++) { dist[i, j] = graph[i, j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Pirms iterācijas sākuma mums ir mazākie attālumi starp visiem virsotņu pāriem, lai mazākie attālumi uzskatītu tikai virsotnes kopā {0, 1, 2, .. k-1} kā starpvirsotnes. ---> Pēc iterācijas beigām virsotne Nr. k tiek pievienots starpvirtņu kopai, un kopa kļūst par {0, 1, 2, .. k} */ ja (k = 0; k< V; k++) { // Pick all vertices as source // one by one for (i = 0; i < V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i, k] + dist[k, j] < dist[i, j]) { dist[i, j] = dist[i, k] + dist[k, j]; } } } } // Print the shortest distance matrix printSolution(dist); } void printSolution(int[, ] dist) { Console.WriteLine( 'Following matrix shows the shortest ' + 'distances between every pair of vertices'); for (int i = 0; i < V; ++i) { for (int j = 0; j < V; ++j) { if (dist[i, j] == INF) { Console.Write('INF '); } else { Console.Write(dist[i, j] + ' '); } } Console.WriteLine(); } } // Driver's Code public static void Main(string[] args) { /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ int[, ] diagramma = { { 0, 5, INF, 10 }, { INF, 0, 3, INF }, { INF, INF, 0 , 1 }, { INF, INF, INF, 0 } }; AllPairShortestPath a = new AllPairShortestPath(); // Funkcijas izsaukums a.floydWarshall(graph); } } // Šī raksta autors // Abdul Mateen Mohammed> Javascript // A JavaScript program for Floyd Warshall All // Pairs Shortest Path algorithm. var INF = 99999; class AllPairShortestPath { constructor() { this.V = 4; } floydWarshall(graph) { var dist = Array.from(Array(this.V), () =>jauns Masīvs(this.V).fill(0)); var i, j, k; // Inicializēt risinājuma matricu // tāda pati kā ievades grafika matrica // Vai arī mēs varam teikt, ka sākotnējās // īsāko attālumu vērtības // ir balstītas uz īsākajiem ceļiem // neņemot vērā starpposma // virsotni priekš (i = 0; i< this.V; i++) { for (j = 0; j < this.V; j++) { dist[i][j] = graph[i][j]; } } /* Add all vertices one by one to the set of intermediate vertices. --->Pirms iterācijas sākuma mums ir mazākie attālumi starp visiem virsotņu pāriem, lai mazākie attālumi uzskatītu tikai virsotnes kopā {0, 1, 2, .. k-1} kā starpvirsotnes. ---> Pēc iterācijas beigām virsotne Nr. k tiek pievienots starpvirtņu kopai, un kopa kļūst par {0, 1, 2, .. k} */ ja (k = 0; k< this.V; k++) { // Pick all vertices as source // one by one for (i = 0; i < this.V; i++) { // Pick all vertices as destination // for the above picked source for (j = 0; j < this.V; j++) { // If vertex k is on the shortest // path from i to j, then update // the value of dist[i][j] if (dist[i][k] + dist[k][j] < dist[i][j]) { dist[i][j] = dist[i][k] + dist[k][j]; } } } } // Print the shortest distance matrix this.printSolution(dist); } printSolution(dist) { document.write( 'Following matrix shows the shortest ' + 'distances between every pair of vertices ' ); for (var i = 0; i < this.V; ++i) { for (var j = 0; j < this.V; ++j) { if (dist[i][j] == INF) { document.write(' INF '); } else { document.write(' ' + dist[i][j] + ' '); } } document.write(' '); } } } // Driver Code /* Let us create the following weighted graph 10 (0)------->(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ var grafiks = [ [0, 5, INF, 10], [INF, 0, 3, INF], [INF, INF, 0, 1] , [INF, INF, INF, 0], ]; var a = new AllPairShortestPath(); // Izdrukāt risinājumu a.floydWarshall(graph); // Šo kodu nodrošina rdtaank.>>PHP(3) | /| 5 | | | | 1 |/ | (1)------->(2) 3 */ $graph = masīvs(masīvs(0, 5, $INF, 10), masīvs($INF, 0, 3, $INF), masīvs($ INF, $INF, 0, 1), masīvs ($INF, $INF, $INF, 0)); // Funkcijas izsaukums floydWarshall($graph, $V, $INF); // Šo kodu sniedz Ryuga ?>>>
Izvade Floida Voršala algoritma sarežģītības analīze: - Laika sarežģītība: O(V3), kur V ir virsotņu skaits grafikā, un mēs izpildām trīs ligzdotas cilpas, kuru katra izmērs ir V
- Palīgtelpa: O(V2), lai izveidotu 2-D matricu, lai saglabātu īsāko attālumu katram mezglu pārim.
Piezīme : Iepriekš minētā programma drukā tikai īsākos attālumus. Mēs varam modificēt risinājumu, lai izdrukātu īsākos ceļus, arī saglabājot priekšgājēja informāciju atsevišķā 2D matricā.
Kāpēc Floyd-Warshall algoritms ir labāks blīviem grafikiem, nevis retajiem grafikiem?
Blīvs grafiks : grafiks, kurā malu skaits ir ievērojami lielāks par virsotņu skaitu.
Rets grafiks : grafiks, kurā malu skaits ir ļoti mazs.
Neatkarīgi no tā, cik malu ir grafikā Floida Voršala algoritms darbojas uz O(V3) reizes, tāpēc tas ir vislabāk piemērots Blīvi grafiki . Retu grafiku gadījumā Džonsona algoritms ir piemērotāks.
Svarīgi intervijas jautājumi saistībā ar Floyd-Warshall:
- Kā noteikt negatīvu ciklu grafikā, izmantojot Floida Voršala algoritmu?
- Kā Floida-Varšala algoritms atšķiras no Dijkstras algoritma?
- Kā Floida-Varšala algoritms atšķiras no Bellmana-Forda algoritma?
Floida-Voršala algoritma pielietojumi reālajā pasaulē:
- Datortīklos algoritmu var izmantot, lai atrastu īsāko ceļu starp visiem tīkla mezglu pāriem. To sauc par tīkla maršrutēšana .
- Lidojumu savienojamība Aviācijas nozarē, lai atrastu īsāko ceļu starp lidostām.
- ĢIS ( Ģeogrāfiskās informācijas sistēmas ) lietojumprogrammas bieži ietver telpisko datu, piemēram, ceļu tīklu, analīzi, lai atrastu īsākos ceļus starp vietām.
- Kleenes algoritms kas ir floyd warshall vispārinājums, var izmantot, lai atrastu regulāru izteiksmi regulārai valodai.