Sadaliet un iekarot ir algoritmisks modelis. Algoritmiskajās metodēs tiek izstrādāts strīds par milzīgu ievadi, sadalot ievadi mazākās daļās, izlemjot problēmu katrā mazajā daļā un pēc tam apvienot pa daļām risinājumus globālā risinājumā. Šo problēmas risināšanas mehānismu sauc par “Skaldi un iekaro” stratēģiju.

Sadalīšanas un iekarošanas algoritms sastāv no strīda, izmantojot šādas trīs darbības.

Sadalietsākotnējo problēmu apakšproblēmu kopumā.Iekarot:Atrisiniet katru apakšproblēmu atsevišķi, rekursīvi.Apvienot:Apkopojiet apakšproblēmu risinājumus, lai iegūtu visas problēmas risinājumu.

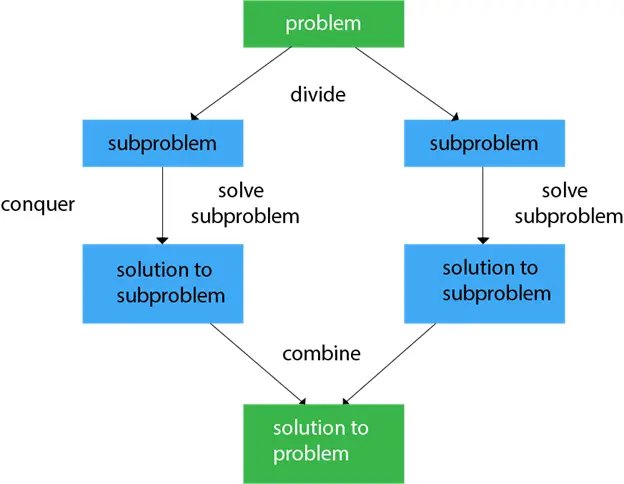
Parasti mēs varam sekot sadali un valdi pieeja trīs soļu procesā.

Piemēri: Konkrētie datoru algoritmi ir balstīti uz Divide & Conquer pieeju:

1. Maksimālā un minimālā problēma
2. Binārā meklēšana
3. Kārtošana (apvienot kārtošanu, ātrā kārtošana)
4. Hanojas tornis.

“Skaldi un valdi” stratēģijas pamati:

Ir divi “Skaldi un iekaro” stratēģijas pamatprincipi:

1. Relāciju formula
2. Apstāšanās nosacījums

1. Relāciju formula: Tā ir formula, ko mēs ģenerējam no dotās tehnikas. Pēc formulas ģenerēšanas mēs pielietojam D&C stratēģiju, t.i., mēs rekursīvi pārtraucam problēmu un atrisinām sadalītās apakšproblēmas.

2. Apstāšanās nosacījums: Kad mēs atrisinām problēmu, izmantojot stratēģiju Divide & Conquer, mums ir jāzina, ka uz cik ilgu laiku mums ir jāpiemēro sadalīt un iekarot. Tātad stāvoklis, kad nepieciešamība apturēt mūsu D&C rekursijas soļus, tiek saukta par apstāšanās nosacījumu.

Skaldi un valdi pieejas pielietojumi:

Tālāk minētie algoritmi ir balstīti uz sadalīšanas un iekarošanas tehnikas koncepciju:

Binārā meklēšana:Binārais meklēšanas algoritms ir meklēšanas algoritms, ko sauc arī par pusintervāla meklēšanu vai logaritmisko meklēšanu. Tas darbojas, salīdzinot mērķa vērtību ar sakārtotā masīvā esošo vidējo elementu. Pēc salīdzināšanas, ja vērtība atšķiras, puse, kurā nevar būt mērķis, galu galā tiks likvidēta, un pēc tam tiks turpināta meklēšana otrā pusē. Mēs vēlreiz apsvērsim vidējo elementu un salīdzināsim to ar mērķa vērtību. Process tiek atkārtots, līdz tiek sasniegta mērķa vērtība. Ja pēc meklēšanas beigām atradām otru pusi tukšu, tad var secināt, ka mērķa masīvā nav.Ātrā šķirošana:Tas ir visefektīvākais šķirošanas algoritms, kas pazīstams arī kā nodalījumu apmaiņas kārtošana. Tas sākas ar pagrieziena vērtības atlasi no masīva, kam seko pārējo masīva elementu sadalīšana divos apakšmasīvos. Sadalījums tiek izveidots, salīdzinot katru elementu ar pagrieziena vērtību. Tas salīdzina, vai elementam ir lielāka vai mazāka vērtība nekā rakursam, un pēc tam kārto masīvus rekursīvi.Sapludināt kārtot:Tas ir šķirošanas algoritms, kas sakārto masīvu, veicot salīdzinājumus. Tas sākas ar masīva sadalīšanu apakšmasīvā un pēc tam rekursīvi kārto katru no tiem. Kad šķirošana ir pabeigta, tās tiek apvienotas atpakaļ.Tuvākais punktu pāris:Tā ir skaitļošanas ģeometrijas problēma. Šis algoritms uzsver tuvākā punktu pāra noskaidrošanu metriskajā telpā, ņemot vērā n punktus, lai attālumam starp punktu pāriem jābūt minimāliem.Štrasena algoritms:Tas ir matricas reizināšanas algoritms, kas nosaukts Volkera Strassen vārdā. Tas ir izrādījies daudz ātrāks nekā tradicionālais algoritms, kad tas darbojas uz lielām matricām.Kūlija-Tūkija ātrās Furjē transformācijas (FFT) algoritms:Ātrās Furjē transformācijas algoritms ir nosaukts J. W. Cooley un John Turkey vārdā. Tas seko 'Skaldi un valdi' pieejai un uzliek O(nlogn) sarežģītību.Karatsuba algoritms ātrai reizināšanai:Tas ir viens no ātrākajiem tradicionālā laika reizināšanas algoritmiem, ko 1960. gada beigās izgudroja Anatolijs Karatsuba un publicēja 1962. gadā. Tas reizina divus n-ciparu skaitļus tādā veidā, samazinot to līdz viencipara skaitlim.

Skaldi un valdi priekšrocības

• “Skaldi un iekarot” mēdz veiksmīgi atrisināt vienu no lielākajām problēmām, piemēram, Hanojas torni, matemātisko mīklu. Ir grūti atrisināt sarežģītas problēmas, par kurām jums nav pamata ideju, taču ar skaldi un valdi pieejas palīdzību tas ir samazinājis pūles, jo tā strādā, sadalot galveno problēmu divās daļās un pēc tam tās atrisinot rekursīvi. Šis algoritms ir daudz ātrāks nekā citi algoritmi.
• Tas efektīvi izmanto kešatmiņu, neaizņemot daudz vietas, jo tas atrisina vienkāršas kešatmiņas apakšproblēmas, nevis piekļūst lēnākajai galvenajai atmiņai.
• Tas ir prasmīgāks nekā tā līdziniece Brute Force tehnika.
• Tā kā šie algoritmi kavē paralēlismu, tas neietver nekādas izmaiņas, un tos apstrādā sistēmas, kas ietver paralēlu apstrādi.

Skaldi un valdi trūkumi

• Tā kā lielākā daļa tā algoritmu ir izstrādāti, iekļaujot rekursiju, tāpēc ir nepieciešama augsta atmiņas pārvaldība.
• Izteikta kopa var pārmērīgi izmantot vietu.
• Tas pat var izraisīt sistēmas avāriju, ja rekursija tiek veikta stingri lielāka par CPU esošo steku.