A Skaitītājs ir ierīce, kas saglabā (un dažreiz parāda), cik reižu konkrēts notikums vai process ir noticis, bieži vien saistībā ar pulksteņa signālu. Skaitītāji tiek izmantoti digitālajā elektronikā skaitīšanas nolūkos, tie var uzskaitīt konkrētu notikumu, kas notiek ķēdē. Piemēram, UP skaitītājā skaitītājs palielina skaitu katrai pulksteņa pieaugošajai malai. Ne tikai skaitot, skaitītājs var sekot noteiktai secībai, pamatojoties uz mūsu dizainu, tāpat kā jebkura nejauša secība 0,1,3,2…. Tās var arī veidot ar flip flops palīdzību. Tos izmanto kā frekvences dalītājus, kur tiek sadalīta noteiktā impulsa viļņu formas frekvence. Skaitītāji ir secīga ķēde, kas skaita impulsu skaitu var būt vai nu binārā koda, vai BCD formā. Skaitītāja galvenās īpašības ir laika noteikšana, secība un skaitīšana. Skaitītājs darbojas divos režīmos
Uz augšu skaitītājs
Leju skaitītājs
Skaitītāja klasifikācija
Skaitītāji ir plaši sadalīti divās kategorijās
- Asinhronais skaitītājs
- Sinhronais skaitītājs
1. Asinhronais skaitītājs
Asinhronajā skaitītājā mēs neizmantojam universālo pulksteni, tikai pirmo flip flopu darbina galvenais pulkstenis, bet pārējās nākamās flip flopa pulksteņa ievadi vada iepriekšējo flip flopu izvade. Mēs to varam saprast, izmantojot šādu diagrammu-
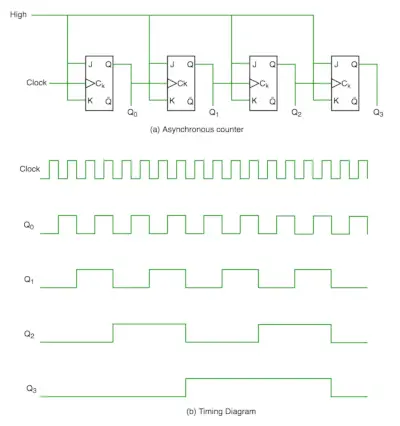
No laika diagrammas ir redzams, ka Q0 mainās, tiklīdz tiek sastapta pulksteņa impulsa pieaugošā mala, Q1 mainās, kad tiek sastapta Q0 augošā mala (jo Q0 ir kā pulksteņa impulss otrajam flip flopam) un tā tālāk. Tādā veidā viļņi tiek ģenerēti caur Q0, Q1, Q2, Q3, tāpēc to sauc arī RIPPLE skaitītājs un sērijas skaitītājs. Pulsācijas skaitītājs ir flip flop kaskādes izkārtojums, kurā viena flip flopa izvade virza nākamā flip flopa pulksteņa ievadi
2. Sinhronais skaitītājs
Atšķirībā no asinhronā skaitītāja, sinhronajam skaitītājam ir viens globālais pulkstenis, kas darbina katru flip flop, lai izvade mainās paralēli. Sinhronā skaitītāja viena priekšrocība salīdzinājumā ar asinhrono skaitītāju ir tā, ka tā var darboties ar augstāku frekvenci nekā asinhronais skaitītājs, jo tam nav kumulatīvās aizkaves, jo katram flip flopam tiek piešķirts viens un tas pats pulkstenis. To sauc arī par paralēlo skaitītāju.
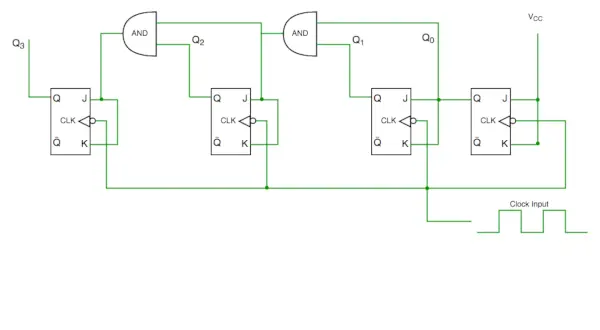
Sinhronā skaitītāja ķēde
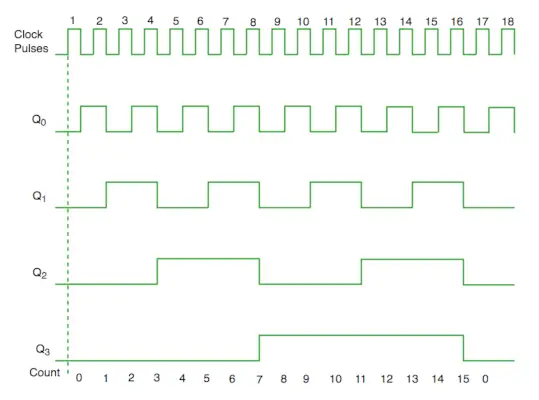
Laika diagrammas sinhronais skaitītājs
No shēmas shēmas mēs redzam, ka Q0 bits reaģē uz katru pulksteņa krītošo malu, savukārt Q1 ir atkarīgs no Q0, Q2 ir atkarīgs no Q1 un Q0, Q3 ir atkarīgs no Q2, Q1 un Q0.
Desmitgades skaitītājs
Desmitgades skaitītājs saskaita desmit dažādus stāvokļus un pēc tam atiestata sākotnējos stāvokļus. Vienkāršs desmitgades skaitītājs skaitīs no 0 līdz 9, bet mēs varam arī izveidot desmitgades skaitītājus, kas var iet cauri jebkuriem desmit stāvokļiem no 0 līdz 15 (4 bitu skaitītājam).
| Pulksteņa impulss | Q3 | Q2 | Q1 | Q0 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 0 | 0 | 0 |
Patiesības tabula vienkāršam desmitgades skaitītājam
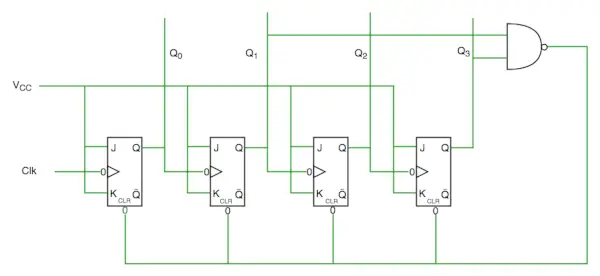
Desmitgades skaitītāja shēmas shēma
No shēmas diagrammas redzam, ka Q3 un Q1 esam izmantojuši nand gate un ievadījuši to, lai notīrītu ievades līniju, jo 10 binārais attēlojums ir -
1010. gads
Un mēs redzam, ka Q3 un Q1 šeit ir 1, ja mēs no šiem diviem bitiem piešķiram NAND, lai notīrītu ievadi, tad skaitītājs būs skaidrs pie 10 un atkal sāksim no sākuma.
Svarīgs punkts : Skaitītājā izmantoto flip flop skaits vienmēr ir lielāks par ( žurnāls2n ) kur n = stāvokļu skaits skaitītājā.
Dažu iepriekšējo gadu vārtu jautājumi vietnē Counters
Q1. Apsveriet daļēju 2 bitu skaitītāja ieviešanu, izmantojot T flip-flops pēc secības 0-2-3-1-0, kā parādīts zemāk.
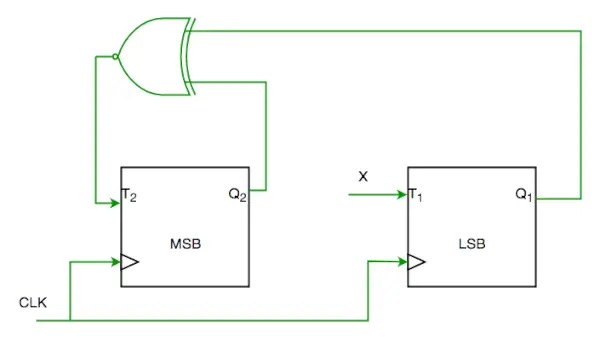
Lai pabeigtu ķēdi, ieejai X jābūt
(A) Q2?
(B) Q2 + Q1
(C) (Q1? Q2)”
(D) Q1? Q2 (GATE-CS-2004)
Risinājums:
No ķēdes mēs redzam
T1=XQ1’+X’Q1—-(1)
UN
T2=(Q2 ? Q1)'—-(2)
UN VĒLAMĀ IZEJA IR 00->10->11->01->00
TĀDĀM IR JĀBŪT X Q1 Q2'+Q1'Q2 APMIERINĀJUMS 1. UN 2.
SO ANS IS (D) DAĻA.
Q2. 4 bitu binārā skaitītāja vadības signāla funkcijas ir norādītas zemāk (kur X ir vienalga)
Skaitītājs ir savienots šādi:
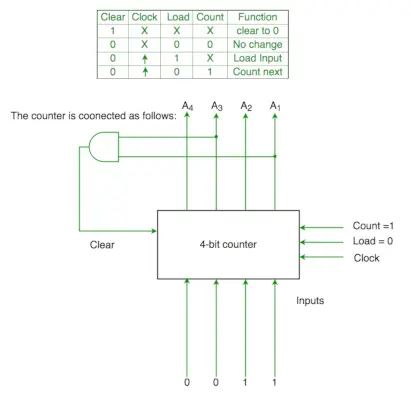
Pieņemsim, ka skaitītāja un vārtu aizkave ir nenozīmīga. Ja skaitītājs sākas ar 0, tas darbojas šādā secībā:
(A) 0,3,4
(B) 0,3,4,5
(C) 0,1,2,3,4
(D) 0,1,2,3,4,5 (GATE-CS-2007)
Risinājums:
Sākotnēji A1 A2 A3 A4 =0000
Clr=A1 un A3
Tātad, kad A1 un A3 abi ir 1, tas atkal pāriet uz 0000
Tādējādi 0000(sākotn.) -> 0001(A1 un A3=0)->0010 (A1 un A3=0) -> 0011(A1 un A3=0) -> 0100 ( A1 un A3=1 )[ skaidrs nosacījums apmierināts] ->0000(sākotn.), tātad tas iet cauri 0->1->2->3->4
Ans ir (C) daļa.
mikrolīts kodols
Viktorīna par digitālo loģiku
Raksta autors Anuj Batham,
