Kausa šķirošana ir šķirošanas tehnika, kas ietver elementu sadalīšanu dažādās grupās vai spainīšos. Šie spaiņi tiek veidoti, vienmērīgi sadalot elementus. Kad elementi ir sadalīti segmentos, tos var kārtot, izmantojot jebkuru citu šķirošanas algoritmu. Visbeidzot, sakārtotie elementi tiek apkopoti sakārtotā veidā.
Kausu kārtošanas algoritms:
Izveidot n iztukšojiet segmentus (Vai sarakstus) un veiciet tālāk norādītās darbības katram masīva elementam arr[i].
- Ievietojiet arr[i] spainī[n*masīvs[i]]
- Kārtojiet atsevišķus segmentus, izmantojot ievietošanas kārtošanu.
- Savienojiet visus sašķirotos spaiņus.
Kā darbojas kausu kārtošana?
Lai ievades masīvā lietotu kausa kārtošanu [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , mēs rīkojamies šādi:
1. darbība: Izveidojiet 10 izmēra masīvu, kurā katrs slots apzīmē spaini.

Spaiņu veidošana šķirošanai
2. darbība: Ievietojiet elementus segmentos no ievades masīva, pamatojoties uz to diapazonu.
Elementu ievietošana spaiņos:
kā pārvērst virkni par int
- Paņemiet katru elementu no ievades masīva.
- Reiziniet elementu ar kausa masīva lielumu (šajā gadījumā 10). Piemēram, elementam 0,23 mēs iegūstam 0,23 * 10 = 2,3.
- Konvertējiet rezultātu par veselu skaitli, kas dod mums segmenta indeksu. Šajā gadījumā 2.3 tiek pārveidots par veselu skaitli 2.
- Ievietojiet elementu spainī, kas atbilst aprēķinātajam indeksam.
- Atkārtojiet šīs darbības visiem ievades masīva elementiem.
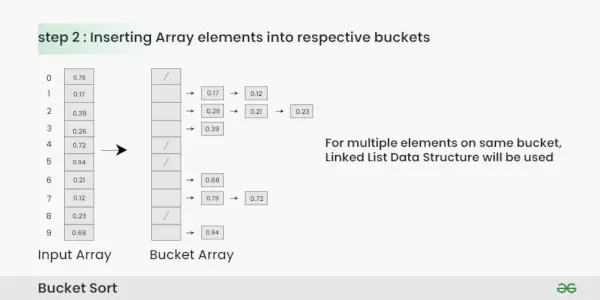
Masīva elementu ievietošana attiecīgajos kausos
3. darbība: Kārtojiet elementus katrā segmentā. Šajā piemērā mēs izmantojam ātro kārtošanu (vai jebkuru stabilu kārtošanas algoritmu), lai kārtotu elementus katrā segmentā.
Elementu kārtošana katrā segmentā:
- Izmantojiet stabilu kārtošanas algoritmu (piemēram, burbuļu kārtošana, sapludināšanas kārtošana), lai kārtotu elementus katrā segmentā.
- Elementi katrā segmentā tagad ir sakārtoti.
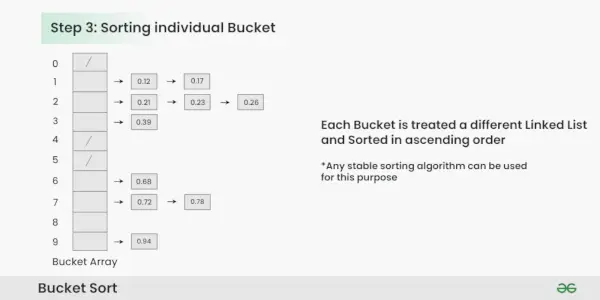
Atsevišķa spaiņa šķirošana
4. darbība: Apkopojiet elementus no katra kausa un ievietojiet tos atpakaļ sākotnējā masīvā.
Elementu vākšana no katra spaiņa:
- Atkārtojiet katru spaini secībā.
- Ievietojiet katru atsevišķu elementu no kausa sākotnējā masīvā.
- Kad elements ir nokopēts, tas tiek noņemts no kausa.
- Atkārtojiet šo procesu visiem spaiņiem, līdz visi elementi ir savākti.
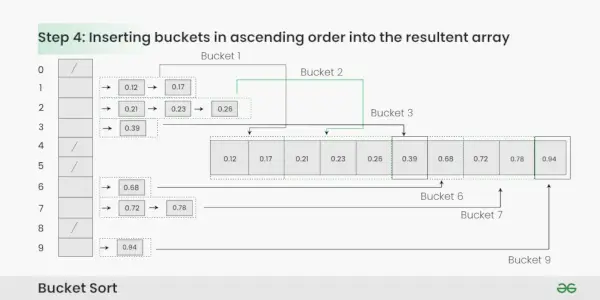
Segmentu ievietošana augošā secībā iegūtajā masīvā
5. darbība: Sākotnējais masīvs tagad satur sakārtotos elementus.
Galīgais sakārtotais masīvs, izmantojot segmentu kārtošanu dotajai ievadei, ir [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].

Atgrieziet sakārtoto masīvu
Kausu kārtošanas algoritma ieviešana:
Tālāk ir sniegta kārtošanas starp kauss ieviešana.
vai android var spēlēt gamepigeonC++
#include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& spainis) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && spainis[j]> taustiņš) { spainis[j + 1] = spainis[j]; j--; } spainis[j + 1] = atslēga; } } // Funkcija kārtot arr[] ar izmēru n, izmantojot kausa kārtošanu void bucketSort(float arr[], int n) { // 1) Izveidot n tukšu kausu vektorub[n]; // 2) Ievietojiet masīva elementus dažādos segmentos priekš (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listspainis) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && bucket.get(j)> taustiņš) { bucket.set(j + 1, bucket.get(j)); j--; } bucket.set(j + 1, taustiņš); } } // Funkcija kārtot arr[] ar izmēru n, izmantojot kausa kārtošanu public static void bucketSort(float[] arr) { int n = arr.length; // 1) Izveidojiet n tukšu spaiņu sarakstu[] spaiņi = jauns ArrayList[n]; for (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 un spainis[j]> taustiņš: spainis[j + 1] = spainis[j] j -= 1 spainis[j + 1] = taustiņš def bucket_sort(arr): n = len(arr) spaiņi = [[] for _ in range(n)] # Ievietojiet masīva elementus dažādos segmentos par num in arr: bi = int(n * num) buckets[bi].append(num) # Kārtot atsevišķus segmentus, izmantojot ievietošanas kārtošanu spaiņiem: insertion_sort (kopa) # Savienot visus segmentus arr[] indekss = 0 segmentam segmentos: skaitam segmentā: arr[indekss] = indeksa skaits += 1 arr = [0,897, 0,565, 0,656, 0,1234, 0,6365, ]0. (arr) print('Sakārtotais masīvs ir:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listspainis) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && spainis[j]> taustiņš) { spainis[j + 1] = spainis[j]; j--; } spainis[j + 1] = atslēga; } } // Funkcija kārtot arr[] ar izmēru n, izmantojot kausa kārtošanu static void BucketSort(float[] arr) { int n = arr.Length; // 1) Izveidojiet n tukšu spaiņu sarakstu[] spaiņi = jauns saraksts[n]; for (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Ievietojiet masīva elementus dažādos segmentos priekš (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && spainis[j]> taustiņš) { spainis[j + 1] = spainis[j]; j--; } spainis[j + 1] = atslēga; } } function bucketSort(arr) { let n = arr.length; let buckets = Array.from({garums: n}, () => []); // Ievietojiet masīva elementus dažādos segmentos priekš (lai i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Izvade
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Kausu kārtošanas algoritma sarežģītības analīze:
Laika sarežģītība: O(n2),
- Ja pieņemam, ka ievietošana spainī prasa O(1) laiku, tad iepriekšminētā algoritma 1. un 2. darbība nepārprotami prasa O(n) laiku.
- O(1) ir viegli iespējams, ja mēs izmantojam saistīto sarakstu, lai attēlotu segmentu.
- 4. darbība aizņem arī O(n) laiku, jo visos segmentos būs n vienumi.
- Galvenais analīzes solis ir 3. solis. Šis solis arī aizņem vidēji O(n) laiku, ja visi skaitļi ir vienmērīgi sadalīti.
Palīgtelpa: O(n+k)
