Leņķis starp diviem vektoriem ir leņķis starp to astēm, un šo leņķi var viegli atrast, izmantojot vektoru formulu krustojumu un punktu reizinājumu. Leņķis starp diviem vektoriem vienmēr ir no 0° līdz 180°.
Šajā rakstā mēs detalizēti uzzināsim par leņķi starp diviem vektoriem, definīcijām, formulām un piemēriem.
Kāds ir leņķis starp diviem vektoriem?
Leņķis starp diviem vektoriem ir leņķis, kas veidojas to astes krustpunktā. Leņķis starp diviem vektoriem var būt akūts, taisns vai neass, atkarībā no vektoru virziena.
Leņķi starp diviem vektoriem nosaka, izmantojot divas formulas:
- Vektoru punktu produkta izmantošana
- Vektoru šķērsprodukta izmantošana
Tas ir izskaidrots zemāk esošajā formulā.
Leņķis starp divām vektoru formulām
Leņķis starp diviem vektoriem ir viegli un visbiežāk atrodams, izmantojot vektoru skalāro reizinājumu.

Divi vektori A un B
Punktu produkts A un B ir dota ar,
vec{A}.vec{B} = |A| |B| cosθ.
Īpaši gadījumi
- Ja leņķis starp vektoriem ir 0 grādi.
Tas ir θ = 0°
⇒ |A| |B| cosθ
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Ja leņķis starp vektoriem ir 180 grādi.
⇒ |A| |B| cosθ
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Ja leņķis starp vektoriem ir 90 grādi.
⇒ |A| |B| cosθ
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0
Formula leņķim starp diviem vektoriem
Leņķa kosinuss starp diviem vektoriem ir vienāds ar divu vektoru atsevišķo sastāvdaļu reizinājuma summu, kas dalīta ar abu vektoru lieluma reizinājumu.
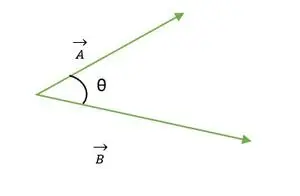
Divi vektori A un B
cosθ=
θ= cos-1
python saraksta inicializācija
Dekarta formā,
A = Axi + Aunj+AArk
B = Bxi + Bunj+BArk
cos θ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})}
Dot produkta īpašības
- Punktu produkts ir komutatīvais
vec{A}.vec{B}=vec{B}.vec{A}
- Dot produkts ir izplatīšanas līdzeklis
vec{A}.(vec{B}+vec{C})=(vec{A}.vec{B}+vec{A}.vec{C}) c++ prototipa funkcija
Leņķis starp diviem vektoriem ir starp 0 ≤ θ ≤ 180. Ja abu vektoru astes vai galviņas sakrīt, tad aprēķina leņķi starp vektoriem.
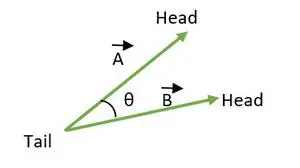
Aste sakrīt
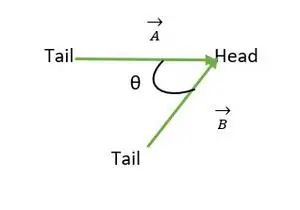
Galva Sakrīt
Problēmu paraugs Leņķis starp diviem vektoriem Formula
1. uzdevums: atrodiet leņķi starp vektoriem (ja tie veido vienādmalu trīsstūri)
- a un b vektori
- b un c vektori
- a un c vektori
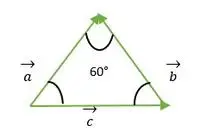
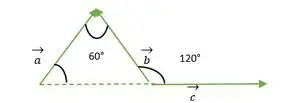
Vienādmalu trīsstūris, ko veido a, b, c vektors
Risinājums:
- a un b vektori
Vektoriem a un b abu vektoru gals sakrīt viens ar otru, tāpēc leņķis starp a un b vektoru ir tāds pats kā leņķis starp vienādmalu trīsstūra divām malām = 60°.
- b un c vektori:
No iepriekš redzamā attēla redzam, ka b un c vektora galva vai aste nesakrīt viens ar otru.
Tātad, izmantojot īpašību - vektors paliek nemainīgs, ja tas tiek pārraidīts paralēli sev.
Vektors c ir nobīdīts paralēli pats sev
Tagad mēs redzam, ka vektoru b un c aste sakrīt viens ar otru, tāpēc ir tāds pats kā ārējais leņķis ar vienādmalu trīsstūri = 120°.
- a un c vektori
A un c aste sakrīt
Vektoriem a un c abu vektoru aste sakrīt viens ar otru, tāpēc leņķis starp a un c vektoru ir tāds pats kā leņķis starp vienādmalu trīsstūra divām malām = 60°.
2. uzdevums: atrodiet leņķus starp vektoriem, ja tie veido vienādsānu taisnleņķa trīsstūri.
- a un b vektors
- b un c vektors
- a un c vektori
Risinājums:
- a un b vektors
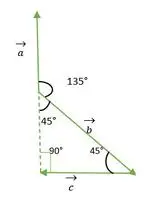
Taisns leņķis Vienādsānu trīsstūris
No iepriekš redzamā attēla redzam, ka a un b vektora galva vai aste nesakrīt viens ar otru. Tātad, izmantojot īpašību - vektors paliek nemainīgs, ja tas tiek pārraidīts paralēli sev.
vektors tiek nobīdīts paralēli pats sev
Tagad a un b vektoru astes sakrīt viena ar otru un veido tādu pašu leņķi kā taisnleņķa vienādsānu trīsstūra ārējais leņķis = 135°.
- b un c vektors
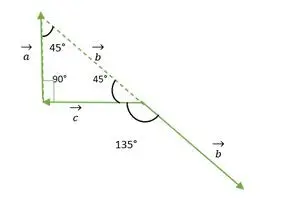
Taisns leņķis vienādsānu trīsstūris
No iepriekš minētā attēla, b un c vektora galva vai astes nesakrīt viens ar otru. Tātad, izmantojot īpašību, vektors paliek nemainīgs, ja tas tiek pārraidīts paralēli pats sev.
b vektors tiek nobīdīts paralēli pats sev
Tagad b un c vektoru astes sakrīt viena ar otru un veido tādu pašu leņķi kā taisnleņķa vienādsānu trīsstūra ārējais leņķis = 135°.
- a un c vektori
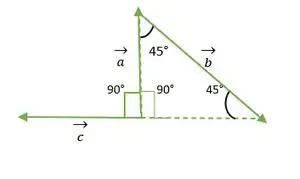
Taisns leņķis Vienādsānu trīsstūris
No iepriekš redzamā attēla a un c vektora galva vai astes nesakrīt viens ar otru. Tātad, izmantojot īpašību - vektors paliek nemainīgs, ja tas tiek pārraidīts paralēli sev.
c vektors tiek pārvietots paralēli sev
Tagad a un c vektoru astes sakrīt viena ar otru un veido tādu pašu leņķi kā vienādsānu trijstūra taisnais leņķis = 90°.
3. uzdevums: Atrodiet leņķi starp vektoriem A = i + j + k un vektoru B = -2i – 2j – 2k.
Risinājums:
No formulas,
A = Axi + Aunj+AArk
B = Bxi + Bunj+BArk
cosθ=
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Šeit, Dotajā jautājumā,
A= i + j + k
B= -2i -2j -2k
Formulā esošo vērtību aizstāšana
⇒ cosθ =
frac{(1.(-2)+1.(-2)+1.(-2))}{(sqrt{1^2+1^2+1^2}×sqrt{(-2)^2+(-2)^2+(-2)^2})} stīgas c⇒ cosθ =
frac{(-2-2-2)}{(sqrt{1+1+1}×sqrt{4+4+4})} ⇒ cosθ =
frac{-6}{(sqrt{3}×sqrt{12})} ⇒ cosθ =
frac{-6}{(sqrt{36})} ⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°
4. uzdevums: atrodiet leņķi starp vektoru A = 3i + 4j un B = 2i + j
Risinājums:
A = Axi + Aunj+AArk
B = Bxi + Bunj+BArk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Šeit ņemot vērā,
A= 3i + 4j + 0k
B= 2i + j + 0k
Formulā esošo vērtību aizstāšana,
⇒ cosθ =
frac{(3.2+4.1+0.0)}{(sqrt{3^2+4^2+0^2}×sqrt{2^2+1^2+0^2})} ⇒ cosθ =
frac{(6+4+0)}{(sqrt{9+16+0}×sqrt{4+1+0})} ⇒ cosθ =
frac{(10)}{(sqrt{25}×sqrt{5})} ⇒ cosθ =
frac{(10)}{(sqrt{125})} ⇒ θ = cos-1(
frac{(10)}{5.(sqrt{5})} )⇒ θ = cos-1(
frac{2}{(sqrt{5})} )
5. uzdevums: atrodiet leņķi starp vektoru A = i + j un vektoru B = j + k.
Risinājums:
No formulas,
A = Axi + Aunj+AArk
B = Bxi + Bunj+BArk
cosθ =
frac{(Ax.Bx+Ay.By+Az.Bz)}{(sqrt{Ax^2+Ay^2+Az^2}×sqrt{Bx^2+By^2+Bz^2})} Šeit, Dotajā jautājumā,
⇒ A = i + j
Salman Khan vecums⇒ B = j + k
⇒ cosθ =
frac{(1.0+1.1+0.1)}{(sqrt{1^2+1^2+0^2}×sqrt{0^2+1^2+1^2})} ⇒ cosθ =
frac{(1)}{(sqrt{1+1+0}×sqrt{0+1+1})} ⇒ cosθ =
frac{1}{(sqrt{2}×sqrt{2})} ⇒ θ = cos-1(1/2)
⇒ θ = 60°