Polinoma nulles ir reālas, iedomātas vai sarežģītas vērtības, ja tās tiek ievietotas polinomā, nevis mainīgā, rezultāts kļūst par nulli (kā arī nosaukums norāda uz nulli). Polinomi tiek izmantoti, lai modelētu dažas fiziskas parādības, kas notiek reālajā dzīvē, tie ir ļoti noderīgi, aprakstot situācijas matemātiski.

Polinoma nulles ir visas x vērtības, kas padara polinomu vienādu ar nulli. Polinoma nulles norāda uz polinoma grafika x-pārtvērumiem. Šajā rakstā mēs apspriedīsim par polinoma nulles, kā tās atrast, faktoru teorēma utt.

Satura rādītājs

• Kas ir polinomu nulles?
• Polinomu formulas nulles
• Kā atrast polinoma nulli?
• Lineāram polinomam
• Kvadrātiskajam polinomam
• Kubiskā polinomam
• Faktoru teorēma
• Attiecība starp nullēm un koeficientu
• Attiecība starp nullēm un koeficientu kvadrātvienādojumam
• Kubiskā vienādojuma nulles un koeficienta saistība
• Vienādojuma veidošana ar polinoma nullēm
• Nulles polinomu grafikā
• Lineārās algebras pamatteorēma
• Saknes daudzveidība
• Raksti, kas saistīti ar polinomu nullēm
• Problēmu paraugi uz polinoma nullēm
• Praktizējiet polinoma nulles

Kas ir polinomu nulles?

Polinomam P(x) mēs sakām, ka x = a ir polinoma nulle, ja P(a) = 0, un visas šādas polinoma nulles parasti sauc par polinoma nullēm. Piemēram, apsveriet f(x) = 3x – 12. Tagad polinomā ievietojiet x = 4, t.i., f(4) = 3×4 – 12 = 0. Tādējādi x = 4 ir polinoma f( x) = 3x – 12.

Piemērs: Ja f(x) = x ³ - 6x ² + 11x – 6, vai x = 1 ir nulle?

Risinājums:

Lai pārbaudītu, vai, ja x = 1 ir nulle no f(x) = x³- 6x²+ 11x – 6 vai nē, ievietojiet x = 1 collā (x)

f(1) = (1)³– 6 × (1)²+ 11×(1) – 6

⇒ f(1) = 1–6 + 11–6 = 12–12 = 0

Tādējādi x = 1 ir f(x) nulle.

Polinomu formulas nulles

Lineāram polinomam, kura forma ir ax + b, tā nulli nosaka ar x = -b/a.

Kvadrātiskajam polinomam ar formu ax²+ bx + c, tā nulle ir dota ar x = {- b ± √D}/2a kur D ir diskriminants, ko dod b²– 4ac.

Kā atrast polinoma nulli?

Mēs varam atrast polinoma nulles dažādu veidu polinomiem, izmantojot dažādas metodes, kas ir apskatītas tālāk.

• Lineāram polinomam
• Kvadrātiskajam polinomam
• Kubiskā polinomam

Lineāram polinomam

Lineārajiem polinomiem nulles atrašana ir visvieglāk. jo ir tikai viena nulle, un to var arī aprēķināt, vienkārši pārkārtojot polinoma pēc pielīdzināšanas polinoma ar 0.

Piemēram, atrodiet nulli lineāram polinomam f(x) = 2x – 7.

Risinājums:

Lai atrastu f(x) nulli, pielīdziniet f(x) ar 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Kvadrātiskajam polinomam

Ir dažādas metodes, lai atrastu kvadrātiskā polinoma saknes vai nulles, piemēram, sadalot vidējo vārdu, kvadrātformulu, kas pazīstama arī kā Šrī Dharačarjas formula, un pabeigt kvadrātu, kas ir nedaudz līdzīgs kvadrātformulai, jo tiek iegūta kvadrātiskā formula. no vispārējā kvadrātvienādojuma kvadrāta pabeigšanas.

Uzziniet vairāk par kvadrātvienādojumu risināšana vai polinomi un kā tos atrisināt. Sekojošie piemēri detalizēti parāda kvadrātpolinomu nulles atrašanas metodi.

1. piemērs: noskaidrojiet nulles P(x) = x ² + 2x – 15.

Atbilde:

x²+ 2x – 15 = 0

⇒ x²+ 5x - 3x - 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

2. piemērs. Atrodiet nulles P(x) = x ² – 16x + 64.

Atbilde:

x²– 16x + 64 = 0

Salīdzinot ar cirvi²+ bx + c = 0,

mēs iegūstam, a = 1, b = -16 un c = 64.

Tādējādi

⇒ x = 8, 8

Kubiskā polinomam

Lai atrastu kubiskā nulles, ir daudz veidu, piemēram, racionālas saknes teorēma un garā dalīšana kopā. Viena no metodēm, kā atrast kubiskā vai jebkura augstākas pakāpes polinoma saknes, ir šāda:

1. darbība: Izmantojiet racionālās saknes teorēmu, lai atrastu iespējamās saknes. i., ja polinomam ir racionāla sakne, tai jābūt p/q dalījumam, kur p ir vesela skaitļa konstante un q ir vadošais koeficients.

2. darbība: Pēc vienas saknes atrašanas sadaliet polinomu ar koeficientu, ko veido šī sakne, izmantojot garo dalīšanu, un ierakstiet polinomu kā koeficienta un dividendes reizinājumu.

3. darbība: Ja koeficients ir kvadrātveida izteiksme, atrisiniet to ar iepriekš minētajām metodēm kvadrātveida polinomiem. Ja tas nav 2. pakāpes polinoms, atkārtojiet 1. un 2. darbību, līdz koeficients kļūst par polinomu ar 2. pakāpi.

4. darbība: 3. darbības rezultāts ir nepieciešamie faktori, un, pielīdzinot koeficientu 0, mēs varam atrast polinoma nulles.

Piemērs: Atrodiet kubiskā polinoma p(x) = x nulles ³ + 2x ² - 5x - 6.

Risinājums:

p(x) = x³+ 2x²- 5x - 6

Tā kā p/q = -6

Pēc racionālās saknes teorēmas visas iespējamās polunoma racionālās saknes ir p/q dalītāji.

Tādējādi dalītāji = ±1, ±2, ±3, ±6

x = -1, p(x), mēs iegūstam

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 - 6 = 0

Tādējādi pēc koeficienta teorēmas x + 1 ir koeficients p(x).

Tādējādi x³+ 2x²– 5x – 6 = (x+1) (x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1) (x-2) (x+3)

Nulles p(x) = 0,

P(x) nulles ir x = -1, x = 2 un x = -3.

Faktoru teorēma

Polinomam P(x) faktoru teorēma nosaka, ka, ja x =a ir P(X) nulle, ja f x – a ir P(x) koeficients. i., abiem tālāk minētajiem nosacījumiem ir jābūt spēkā.

• Ja a ir P(x) nulle, tad x-a būs P(x) koeficients.
• Ja x−a ir P(x) koeficients, tad a būs P(x) nulle

To var pārbaudīt, aplūkojot iepriekšējos piemērus. Faktoru teorēma var novest pie dažiem interesantiem rezultātiem, kas ir šādi:

1. rezultāts: Ja P(x) ir n pakāpes polinoms un r ir P(x) nulle, tad P(x) var uzrakstīt šādā formā:

P(x) = (x – r) Q(x)

Kur Q(x) ir n-1 pakāpes polinoms, un to var noskaidrot, dalot P(x) ar (x – r).

2. rezultāts: Ja P(x) = (x-r)Q(x) un x = t ir Q(x) nulle, tad x = t arī būs P(x) nulle.

Lai pārbaudītu iepriekš minēto faktu,

Pieņemsim, ka t ir nulle Q (x), kas nozīmē, ka Q (t) = 0.

Mēs zinām, ka r ir polinoma P(x) nulle, kur P(x) = (x – r) Q(x),

Tātad mums ir jāpārbauda, ​​vai x = t ir arī P(x) nulle, ieliksim x = t P(x)

⇒ P(t) = (t – r) Q(t) = 0

Tātad, x = t ir arī nulle P(x).

Līdz ar to pierādīts.

Attiecība starp nullēm un koeficientu

Saistība starp nullēm un kvadrātvienādojuma un kubiskā vienādojuma koeficientu ir aplūkota turpmāk.

Attiecība starp nullēm un koeficientu kvadrātvienādojumam

Formas ax kvadrātvienādojumam²+ bx + c = 0, ja kvadrātvienādojuma divas nulles ir α un β, tad

• Saknes summa = α + β = -b/a
• Sakņu reizinājums = α × β = c/a

Kubiskā vienādojuma nulles un koeficienta saistība

Ja α, β un γ ir kubiskā polinoma asis sakne³+ bx²+ cx + d = 0, tad attiecību starp tā nullēm un koeficientiem uzrāda šādi:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Vienādojuma veidošana ar polinoma nullēm

• Kvadrātiskajam polinomam ar nullēm α un β kvadrātisko polinomu nosaka ar

x ² – (a + b)x + ab .

• Kubiskajam polinomam ar trim nullēm α, β un γ kubiskā polinomu aprēķina ar

x ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

Nulles polinomu grafikā

Jebkura polinoma grafikā y = f(x) reālās nulles ir punkts, kurā grafiks krustojas vai pieskaras x asij. (kā grafiks ar iedomātu nulli nekad negriež x asi). Citiem vārdiem sakot, ja kubiskajam polinomam ir 3 reāli risinājumi, tad šī kubiskā polinoma grafiks trīs reizes krustojas ar x asi, bet, ja kādam kubiskajam polinomam ir tikai viens reāls risinājums, tad tas grafs griež tikai x asi. vienreiz.

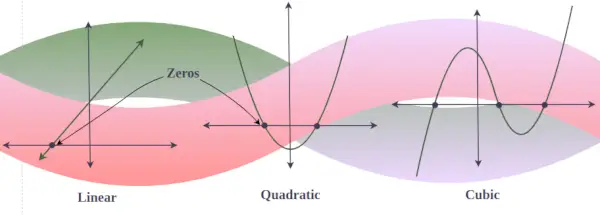
Lineārās algebras pamatteorēma

Ja P(x) ir n pakāpes polinoms, tad P(x) būs tieši n nulles, no kurām dažas var atkārtoties.

Tas nozīmē, ka, ja mēs uzskaitām visas nulles un katru vienu k reizes, kad k ir tās daudzkārtība. Sarakstā mums būs tieši n skaitļi. Tas var būt noderīgi, jo tas var sniegt mums priekšstatu par to, cik nullēm vajadzētu būt polinomā. Tātad mēs varam beigt meklēt nulles, kad esam sasnieguši vajadzīgo nulles skaitu.

Saknes daudzveidība

Pieņemsim, ka mums ir polinoms P(x) = 0, kas faktorizējas

P(x) = (x – r) ^k (x–a) ^m

Ja r ir polinoma nulle un tā vārda eksponents, kas radīja sakni, ir k, tad mēs sakām, ka r ir daudzkārtība k . Bieži tiek sauktas nulles ar reizinājumu 1 vienkārši nulles un nulles ar reizinājumu 2 sauc par polinoma dubultsaknēm.

Piemērs: P(x) ir 5. pakāpes polinoms, kas jums ir faktorizēts. Uzskaitiet saknes un to daudzveidību.

P(x) = 5x ⁵ -20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x–2) ³

Risinājums:

Dots, P(x) = 5(x+1)²(x–2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Lai atrastu nulles, P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Ņemiet vērā, ka -1 notiek divas reizes kā nulle, tāpēc tā reizinājums ir 2, bet nulles reizinājums 2 ir 3.

Raksti, kas saistīti ar polinomu nullēm

• Polinoms
• Kvadrātvienādojuma saknes
• Algebriskā izteiksme

Problēmu paraugi uz polinoma nullēm

1. uzdevums: ņemot vērā, ka x = 2 ir nulle no P(x) = x ³ +2x ² −5x−6. Atrodiet pārējās divas nulles.

Risinājums:

No fundamentālās teorēmas, kuru mēs pētījām iepriekš, mēs varam teikt, ka P(x) būs 3 nulles, jo tas ir trīs grādu polinoms. Viens no tiem ir x = 2.

Tātad mēs varam pārrakstīt P (x),

P(x) = (x – 2) Q(x)

Lai atrastu pārējās divas nulles, mums ir jānoskaidro Q (x).

Q(x) var uzzināt, dalot P(x) ar (x-2).

Pēc dalīšanas Q(x) izrādās,

Q(x) = x²+ 4x + 3

Atlikušās divas nulles var uzzināt no tā,

Q(x) = x²+ 3x + x + 3

⇒ x(x+3)+1(x+3)

ja vēl paziņojums java

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Tādējādi pārējās divas nulles ir x = -1 un x = -3.

2. uzdevums: ņemot vērā, ka x = r ir polinoma nulle, uzziniet pārējās polinoma nulles.

P(x) = x ³ -6x ² −16x; r = −2

Risinājums:

Mēs zinām, ka x = -2 ir nulle,

Tātad P(x) var pārrakstīt šādi: P(x) = (x + 2) Q(x) {izmantojot dalīšanas algoritmu}

Tagad, lai atrastu Q(x), mēs darām to pašu, ko darījām iepriekšējā jautājumā, sadalām P(x) ar (x + 2).

Mēs saņemam,

Q(x) = x²- 8x

Tagad, lai atrastu pārējās divas nulles, koeficientu Q(x)

Q(x) = x (x – 8) = 0

Tātad nulles ir x = 0, 8.

Tādējādi mums ir trīs nulles, x = -2, 0, 8.

3. uzdevums: atrodiet polinoma nulles, 4x ³ -3x ² -25x-6 = 0

Risinājums:

Triks, lai atrisinātu polinoma vienādojumus ar 3. pakāpi,

Atrodiet mazāko veselo skaitli, kas var padarīt polinoma vērtību 0, sāciet ar 1, -1, 2 un tā tālāk...

mēs atklājam, ka pie x = -2 izteiksmes vērtība ir nulle.

Tādējādi viena no saknēm ir -2.

Saskaņā ar faktoru teorēmu, ja a ir viena no polinoma nullēm, tātad (x-a) ir dotā polinoma faktors.

Tādējādi pēc šī {x – (-2)} = (x+2) ir koeficients pof virs polinoma.

Mēs iegūstam kvadrātvienādojumu un tur jau ir nulles.

(4x²-11x-3) (x+2) = 0

Faktorizēt kvadrātvienādojumu,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

4. uzdevums: atrodiet polinoma nulles, 4x ⁶ - 16x ⁴ = 0

Risinājums:

Polinomam ir līdz 6. pakāpei, tātad pastāv 6 polinoma nulles.

4x⁴(x²-4) = 0

4x⁴(x²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Tāpēc x= 0, 0, 0, 0, 2, -2

5. uzdevums: Atrodiet polinoma funkcijas f(x) = x nulles ³ - 2x ² – 5x + 6

Risinājums:

Lai atrastu šī polinoma nulles, mēs iestatām f(x) = 0 un atrisinām x:

f(x) = x³- 2x²– 5x + 6 = 0

Tā kā d/a = 6

Saskaņā ar racionālās saknes teorēmu visas iespējamās polunoma racionālās saknes ir:

d/a dalītāji = ±1, ±2, ±3, ±6

x = 1, p(x), mēs iegūstam

f(1) = (1)³– 2(1)²– 5 (1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Tādējādi pēc faktoru teorēmas x – 1 ir koeficients p(x).

Tādējādi x³+ 2x²– 5x – 6 = (x-1) (x²-x - 6)

x³+ 2x²– 5x – 6 = (x-1) (x+2) (x-3)

Nulles p(x) = 0,

P(x) nulles ir x = 1, x = -2 un x = 3.

Praktizējiet polinoma nulles

1. Atrodiet visas polinoma f(x) = x nulles ³ - 6x ² + 11x – 6

2. Noteikt visas polinoma nulles g(x) = 2x ⁴ - 7x ³ + 3x ² + 4x - 4

3. Atrodiet polinoma h(x) = x nulles ⁵ - 3x ⁴ + 2x ³ - 6x ² + x + 2

4. Noteikt visas polinoma nulles p(x) = 3x ⁴ - 16x ³ + 18x ² + 16x – 12.

Bieži uzdotie jautājumi par polinoma nullēm

Kas ir polinoma nulles?

Šīs reālās vērtības polinoma vērtībai kļūst par 0, t.i., ja p(x) ir polinoms un p(a) = 0, tad x = a ir p(x) nulle.

Kā atrast polinoma nulles?

Ir dažādas metodes dažādiem polinomiem, lai atrastu nulles, piemēram, vidējā termiņa kvadrātiskā izliešana un kvadrātiskā formula. Lineārai, vienkāršai mainīgo pārkārtošanai un kubiskajai mēs izmantojam racionālās saknes teorēmas, garās dalīšanas, faktoru teorēmas un atlikuma teorēmas kombināciju.

Vai polinomā var būt vairāk nekā viena nulle?

Jā, polinomā var būt vairāk nekā viena nulle, patiesībā n grādu polinomā var būt ne vairāk kā n reālas nulles.

Kāda ir polinoma nulles daudzkārtība?

Faktorizācijas procesā polinoma viens faktors vai viena nulle pēc tam vairākas reizes sanāca faktors vai nulle, ko sauc par šīs saknes daudzveidību.

Kas ir algebras pamatteorēma?

Algebras stāvokļu pamatteorēma Ja P(x) ir n pakāpes polinoms, tad P(x) būs tieši n nulles, no kurām dažas var atkārtoties.

Vai polinomam ar grādu n vienmēr ir n īstās saknes?

Nē, polinomam ar pakāpi n ne vienmēr ir n reālas saknes, jo dažas saknes var būt iedomāti vai kompleksi skaitļi.

Kas ir nulles polinoma pakāpe?

Nulles polinoma pakāpe ir nulle.