Z-SCORE STATISTIKĀ - DATU ZINĀTNE

Z-Score statistikā ir mērījums, cik standarta novirzes datu punktam ir no sadalījuma vidējā. Atradīsim z punktu statistikā. Z-rezultāts 0 norāda, ka datu punkta rezultāts ir tāds pats kā vidējais rezultāts. Pozitīvs z rādītājs norāda, ka datu punkts ir virs vidējā, savukārt negatīvs z rādītājs norāda, ka datu punkts ir zem vidējā.

Z-punkta aprēķināšanas formula ir šāda: z = (x – μ)/ p

Kur:

x: ir testa vērtība
m: ir vidējais
pie: ir standarta vērtība

Šajā rakstā mēs apspriedīsim šādus jēdzienus:

Satura rādītājs

Kas ir Z-Score?
Kā aprēķināt Z rezultātu?
Z-score raksturojums
Aprēķiniet novirzes, izmantojot Z score vērtību
Z-Score ieviešana Python
Z-score pielietojums
Z rezultāti salīdzinājumā ar standarta novirzi
Kāpēc Z rezultātus sauc par standarta rādītājiem?

Kas ir Z-Score?

Z-rezultāts, kas pazīstams arī kā standarta rādītājs, parāda datu punkta novirzi no vidējā, izsakot to kā standarta novirzes virs vai zem vidējā. Tas sniedz mums priekšstatu par to, cik tālu datu punkts ir no vidējā. Tādējādi Z-score mēra kā standarta novirzi no vidējā. Piemēram, Z rezultāts 2 norāda, ka vērtība ir 2 standarta novirzes attālumā no vidējās vērtības. Lai izmantotu z rezultātu, mums jāzina populācijas vidējais rādītājs (μ) un arī populācijas standartnovirze (σ).

Z-score formula

Z-rezultātu var aprēķināt, izmantojot šādu formulu.

z = (X – μ) / p

kur,

z = Z rezultāts
X = elementa vērtība
μ = iedzīvotāju vidējais rādītājs
σ = populācijas standartnovirze

Kā aprēķināt Z rezultātu?

Mums ir dots populācijas vidējais (μ), populācijas standartnovirze (σ) un novērotā vērtība (x) problēmas paziņojumā, aizstājot to pašu Z-score vienādojumā, iegūst Z-score vērtību. Atkarībā no tā, vai dotais Z-score ir pozitīvs vai negatīvs, mēs varam izmantot pozitīva Z-tabula vai negatīva Z tabula pieejams tiešsaistē vai statistikas mācību grāmatas aizmugurē pielikumā.

1. piemērs:

Jūs kārtojat GATE eksāmenu un iegūstat 500 punktus. Vidējais GATE punktu skaits ir 390, un standarta novirze ir 45. Cik labi jūs uzrādījāt testu salīdzinājumā ar vidējo testa kārtotāju?

Risinājums:

Iepriekš minētajā jautājuma paziņojumā ir viegli pieejami šādi dati

Neapstrādāts rezultāts/novērotā vērtība = X = 500

Vidējais rezultāts = μ = 390

Standarta novirze = σ = 45

Izmantojot z rezultāta formulu,

ja vēl bash

z = (X – μ) / p

z = (500–390) / 45

z = 110/45 = 2,44

Tas nozīmē, ka jūsu z rezultāts ir 2.44 .

Tā kā Z rezultāts ir pozitīvs 2,44, mēs izmantosim pozitīvo Z tabulu.

Tagad apskatīsim Z tabula (CC-BY), lai uzzinātu, cik labi jūs ieguvāt punktus salīdzinājumā ar citiem testa dalībniekiem.

Izpildiet tālāk sniegtos norādījumus, lai tabulā atrastu varbūtību.

Šeit, z rezultāts = 2,44, kuras i norāda, ka datu punkts ir par 2,44 standarta novirzēm virs vidējā.

Pirmkārt, kartējiet pirmos divus ciparus 2.4 uz Y ass.
Tad pa X asi karte 0.04
Savienojiet abas asis. Abu krustpunkts sniegs jums kumulatīvo varbūtību, kas saistīta ar jūsu meklēto Z rezultāta vērtību

[Šī varbūtība apzīmē laukumu zem standarta normālās līknes pa kreisi no Z punkta]

gimp aizstāt krāsu

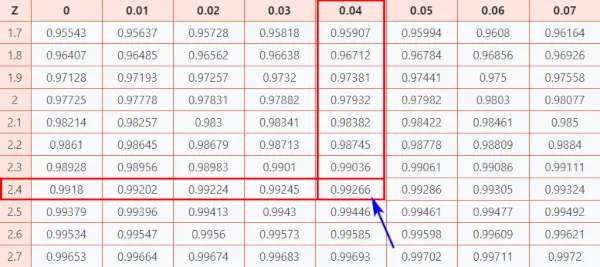
Normāla sadalījuma tabula

Tā rezultātā jūs iegūsit galīgo vērtību, kas ir 0,99266 .

Tagad mums ir jāsalīdzina mūsu sākotnējais rezultāts 500 GATE eksāmenā ar vidējo partijas punktu skaitu. Lai to izdarītu, mums ir jāpārvērš kumulatīvā varbūtība, kas saistīta ar Z rezultātu, par procentuālo vērtību.

0,99266 × 100 = 99,266%

Visbeidzot, jūs varat teikt, ka esat veicis labāk nekā gandrīz 99% citiem testa kārtotājiem.

2. piemērs : Kāda ir iespējamība, ka skolēns iegūs punktus no 350 līdz 400 (ar vidējo punktu skaitu μ 390 un standarta novirzi σ 45)?

Risinājums:

Minimālais rezultāts = X₁= 350

Maksimālais rezultāts = X₂= 400

Izmantojot z rezultāta formulu,

Ar₁= (X1 – m) / p

Ar₁= (350–390) / 45

Ar₁= -40/45 = -0,88

Ar₂= (X₂– m) / lpp

z2 = (400–390) / 45

Ar₂= 10/45 = 0,22

Tā kā z1 ir negatīvs, mums būs jāaplūko negatīvs Z-tabula un atklāj, ka kumulatīvā varbūtība p1, pirmā varbūtība, ir 0,18943 .

Ar₂ir pozitīvs, tāpēc mēs izmantojam pozitīvu Z tabulu, kas iegūst kumulatīvo varbūtību p₂no 0,58706 .

Galīgo varbūtību aprēķina, no p atņemot p1₂:

p = p₂– lpp₁

p = 0,58706 – 0,18943 = 0,39763

Varbūtība, ka skolēns iegūs punktus no 350 līdz 400, ir 39,763% (0,39763 * 100).

Z-score raksturojums

Z rādītāja lielums atspoguļo to, cik tālu datu punkts ir no vidējā standarta novirzes izteiksmē.
Elements, kura z-rezultāts ir mazāks par 0, norāda, ka elements ir mazāks par vidējo.
Z-scores ļauj salīdzināt datu punktus no dažādiem sadalījumiem.
Elements, kura z-rezultāts ir lielāks par 0, norāda, ka elements ir lielāks par vidējo.
Elements, kura z-rezultāts ir vienāds ar 0, norāda, ka elements ir vienāds ar vidējo.
Elements, kura z-rezultāts ir vienāds ar 1, norāda, ka elements ir par 1 standarta novirzi lielāka par vidējo; z-rezultāts, kas vienāds ar 2, 2 standarta novirzes, kas ir lielākas par vidējo, un tā tālāk.
Elements, kura z-rezultāts ir vienāds ar -1, norāda, ka elements ir par 1 standarta novirzi mazāks par vidējo; z rezultāts, kas vienāds ar -2, 2 standarta novirzes mazākas par vidējo, un tā tālāk.
Ja elementu skaits dotajā kopā ir liels, tad aptuveni 68% elementu z-rezultāts ir no -1 līdz 1; apmēram 95% z-rezultāts ir no -2 līdz 2; aptuveni 99% gadījumu z-rezultāts ir no -3 līdz 3. Tas ir pazīstams kā empīriskais likums, un tas norāda datu procentuālo daļu, kas atbilst noteiktām standarta novirzēm no vidējā normālā sadalījumā, kā parādīts tālāk esošajā attēlā.

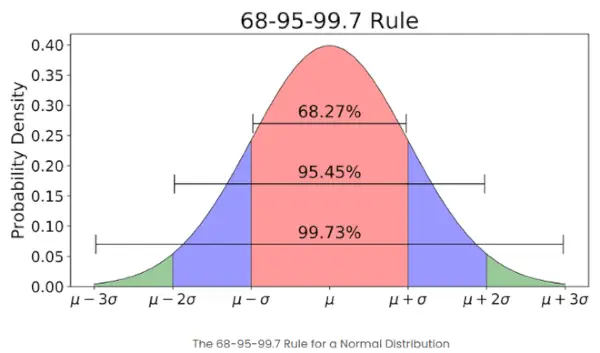
Empīriskais noteikums normālā sadalījumā

Aprēķiniet novirzes, izmantojot Z score vērtību

Mēs varam aprēķināt izņēmumus datos, izmantojot datu punktu z-score vērtību. Darbības, kas jāveic, lai ņemtu vērā izņēmuma datu punktu, ir šādas:

Sākumā mēs apkopojam datu kopu, kurā vēlamies redzēt novirzes
Mēs aprēķināsim datu kopas vidējo un standarta novirzi. Šīs vērtības tiks izmantotas, lai aprēķinātu katra datu punkta z-score vērtību.
Mēs aprēķināsim z-score vērtību katram datu punktam. Z-score vērtības aprēķināšanas formula būs tāda pati kā
Z = frac{{X – mu}}{{sigma}}
kur X būs datu punkts, μ ir datu vidējais lielums un σ ir datu kopas standarta novirze.
Mēs noteiksim z-score robežvērtību, pēc kuras datu punktu varētu uzskatīt par novirzi. Šī robežvērtība ir hiperparametrs, ko mēs izlemjam atkarībā no mūsu projekta.
Datu punkts, kura z score vērtība ir lielāka par 3, nozīmē, ka datu punkts nepieder datu kopas 99,73 % punktam.
Jebkurš datu punkts, kura z rādītājs ir lielāks par mūsu noteikto robežvērtību, tiks uzskatīts par novirzi.

Pārbaudiet: Z rezultāts izņēmuma noteikšanai

Z-Score ieviešana Python

Mēs varam izmantot Python, lai aprēķinātu datu kopas datu punktu z-score vērtību. Mēs arī izmantosim numpy bibliotēku, lai aprēķinātu datu kopas vidējo un standarta novirzi.

Python3

 import numpy as np def calculate_z_score(data): # Mean of the dataset mean = np.mean(data) # Standard Deviation of tha dataset std_dev = np.std(data) # Z-score of tha data points z_scores = (data - mean) / std_dev return z_scores # Example dataset dataset = [3,9, 23, 43,53, 4, 5,30, 35, 50, 70, 150, 6, 7, 8, 9, 10] z_scores = calculate_z_score(dataset) print('Z-Score :',z_scores) # Data points which lies outside 3 standard deviatioms are outliers # i.e outside range of99.73% values outliers = [data_point for data_point,  z_score in zip(dataset, z_scores) if z_score>3] print(f'
Izvirzes datu kopā ir {outliers}')>

Izvade:

Z rezultāts : [-0,7574907 -0,59097335 -0,20243286 0,35262498 0,6301539 -0,72973781
-0,70198492 -0,00816262 0,13060185 0,54689523 1,10195307 3,32218443
-0,67423202 -0,64647913 -0,61872624 -0,59097335 -0,56322046]
Ārpuse datu kopā ir [150]

Z-score pielietojums

Z rezultātus bieži izmanto funkciju mērogošanai, lai dažādas funkcijas apvienotu vienā mērogā. Funkcijas normalizēšana nodrošina, ka tām ir nulles vidējā un vienību dispersija, kas var būt noderīga noteiktiem mašīnmācīšanās algoritmiem, īpaši tiem, kas paļaujas uz attāluma mērījumiem.
Z rādītājus var izmantot, lai datu kopā identificētu novirzes. Datu punktus, kuru Z rezultāti pārsniedz noteiktu slieksni (parasti 3 standarta novirzes no vidējā), var uzskatīt par novirzēm.
Z rādītājus var izmantot anomāliju noteikšanas algoritmos, lai identificētu gadījumus, kas ievērojami atšķiras no paredzamās darbības.
Z-vērtējumus var izmantot, lai pārveidotu šķībo sadalījumu normālākos sadalījumos.
Strādājot ar regresijas modeļiem, var analizēt atlikuma Z punktus, lai pārbaudītu homoskedasticitāti (pastāvīgu atlikumu dispersiju).
Z-vērtējumus var izmantot funkciju mērogošanā, aplūkojot to standarta novirzes no vidējā.

Z rezultāti salīdzinājumā ar standarta novirzi

Z- Rezultāts	Standarta novirze
Pārveidojiet neapstrādātus datus standartizētā mērogā.	Mēra variāciju vai izkliedes apjomu vērtību kopā.
Atvieglo dažādu datu kopu vērtību salīdzināšanu, jo tās atņem sākotnējās mērvienības. runas in powershell	Standarta novirze saglabā sākotnējās mērvienības, padarot to mazāk piemērotu tiešiem datu kopu salīdzinājumiem ar dažādām vienībām.
Norādiet, cik tālu datu punkts ir no vidējā standarta novirzes izteiksmē, nodrošinot datu punkta relatīvās pozīcijas mērījumu sadalījumā.	Izteikts tajās pašās vienībās kā sākotnējie dati, nodrošinot absolūtu mērījumu par to, cik vērtības ir sadalītas ap vidējo

Z- Rezultāts

Standarta novirze

Pārveidojiet neapstrādātus datus standartizētā mērogā.

Mēra variāciju vai izkliedes apjomu vērtību kopā.

Atvieglo dažādu datu kopu vērtību salīdzināšanu, jo tās atņem sākotnējās mērvienības.

runas in powershell

Standarta novirze saglabā sākotnējās mērvienības, padarot to mazāk piemērotu tiešiem datu kopu salīdzinājumiem ar dažādām vienībām.

Norādiet, cik tālu datu punkts ir no vidējā standarta novirzes izteiksmē, nodrošinot datu punkta relatīvās pozīcijas mērījumu sadalījumā.

Izteikts tajās pašās vienībās kā sākotnējie dati, nodrošinot absolūtu mērījumu par to, cik vērtības ir sadalītas ap vidējo

Pārbaudiet: Z rezultātu tabula

Kāpēc Z rezultātus sauc par standarta rādītājiem?

Z rezultātus sauc arī par standarta rādītājiem, jo tie standartizē nejaušā mainīgā lieluma vērtību. Tas nozīmē, ka standartizēto punktu saraksta vidējais rādītājs ir 0 un standarta novirze 1,0. Z rezultāti arī ļauj salīdzināt dažādu veidu mainīgo lielumus. Tas ir tāpēc, ka viņi izmanto relatīvo stāvokli, lai vienādotu dažādu mainīgo vai sadalījumu rezultātus.

Z-rādītājus bieži izmanto, lai salīdzinātu mainīgo ar standarta normālo sadalījumu (ar μ = 0 un σ = 1).

Z-Score statistikā — FAQ

Kāda ir pozitīvo un negatīvo Z punktu nozīme?

Pozitīvie Z rezultāti norāda vērtības, kas pārsniedz vidējo, savukārt negatīvie Z scores norāda vērtības, kas ir zemākas par vidējo. Zīme atspoguļo novirzes virzienu no vidējā.

Ko nozīmē Z-rezultāts 0?

Z-score 0 norāda, ka datu punkta vērtība ir precīzi datu kopas vidējā vērtībā. Tas liecina, ka datu punkts nav ne virs, ne zem vidējā.

Kāds ir noteikums 68-95-99.7 attiecībā uz Z-scores?

Noteikums 68-95-99.7, kas pazīstams arī kā empīriskais noteikums, nosaka, ka:

Apmēram 68% datu ir 1 standarta novirzes robežās no vidējā.
Apmēram 95% ietilpst 2 standarta novirzēs.
Apmēram 99,7% ietilpst 3 standartnoviržu robežās.

Vai Z-scores var izmantot neparastiem sadalījumiem?

Z-scores ir balstītas uz pieņēmumu, ka dati atbilst normālam sadalījumam. Tomēr praksē Z-scores ir izdevīgi datiem, kas atbilst normālam sadalījumam. Lai gan Z-scores var aprēķināt jebkuram sadalījumam, to interpretācija kļūst mazāk uzticama un vienkārša, ja tiek apstrādāti dati, kas nav izplatīti.

Kā Z-scores var izmantot reālās dzīves situācijās?

Z-Scores ir dažādas lietojumprogrammas, piemēram, finansēs portfeļa analīzei, izglītība standartizētai testēšanai, veselība klīniskiem novērtējumiem un daudz ko citu. Tie nodrošina standartizētu pasākumu datu salīdzināšanai un interpretācijai.