Prizma ir trīsdimensiju cieta figūra ar diviem identiskiem galiem. To veido plakanas malas, līdzīgas pamatnes un vienādi šķērsgriezumi. Tās skaldnes ir paralelogrami vai taisnstūri bez pamatnēm. Tādu prizmu, kurai ir trīs taisnstūra skaldnes un divas paralēlas trīsstūra pamatnes, sauc par trīsstūrveida prizmu. Trīsstūrveida pamatnes ir savienotas ar sānu virsmām, kas atrodas paralēli viena otrai.

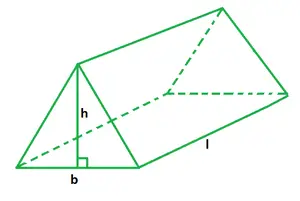
Trīsstūrveida prizmas formulas tilpums

Trīsstūrveida prizmas tilpums tiek definēts kā telpa tajā vai tās aizpildītā telpa. Lai aprēķinātu tās tilpumu, ir tikai jāzina trīsstūrveida prizmas pamatlaukums un augstums. Trīsstūrveida prizmas tilpums ir vienāds ar pamatnes laukuma un prizmas augstuma reizinājumu, ko sauc arī par prizmas garumu. Trīsstūra prizmas pamatlaukums ir vienāds ar pusi no trīsstūra pamatnes un tās augstuma reizinājuma.

Formula

V = (1/2) × b × h × l

kur,

b ir trīsstūra pamatne,

h ir prizmas augstums,

l ir prizmas garums.

Problēmu paraugi

1. uzdevums. Atrodiet trīsstūrveida prizmas tilpumu, ja tās pamatne ir 6 cm, augstums ir 8 cm un garums ir 12 cm.

Risinājums:

Mums ir b = 6, h = 8 un l = 12.

java garš līdz virknei

Izmantojot formulu, kas mums ir,

V = (1/2) × b × h × l

= (1/2) × 6 × 8 × 12

= 3 × 8 × 12

= 288 kub. cm

2. uzdevums. Atrodiet trīsstūrveida prizmas tilpumu, ja tās pamatne ir 5 cm, augstums ir 7 cm un garums ir 8 cm.

Risinājums:

Mums ir b = 5, h = 7 un l = 8.

Izmantojot formulu, kas mums ir,

V = (1/2) × b × h × l

= (1/2) × 5 × 7 × 8

= 5 × 7 × 4

= 140 cu. cm

3. uzdevums. Atrodiet trīsstūra prizmas garumu, ja tās pamatne ir 6 cm, augstums ir 9 cm un tilpums ir 98 cu. cm.

Risinājums:

ko nozīmē xd

Mums ir b = 6, h = 9 un V = 98.

Izmantojot formulu, kas mums ir,

V = (1/2) × b × h × l

=> 98 = (1/2) × 6 × 9 × l

reakcijas tabula

=> 196 = 27l

=> l = 196/27

=> l = 7,25 cm

4. uzdevums. Atrodiet trīsstūrveida prizmas augstumu virs jūras līmeņa, ja tās pamatne ir 8 cm, garums ir 14 cm un tilpums ir 504 cu. cm.

Risinājums:

Mums ir b = 8, l = 14 un V = 504.

Izmantojot formulu, kas mums ir,

V = (1/2) × b × h × l

=> 504 = (1/2) × 8 × h × 14

=> 504 = 56h

=> h = 504/56

=> h = 9 cm

5. uzdevums. Atrodiet trīsstūra prizmas pamatnes laukumu, ja tās garums ir 18 cm, augstums ir 10 cm un tilpums ir 450 cu. cm.

Risinājums:

dfa piemēri

Mums ir l = 18, h = 10 un V = 450.

Izmantojot tilpuma formulu, kas mums ir,

V = (1/2) × b × h × l

=> 450 = (1/2) × b × 10 × 18

=> 450 = 90b

=> b = 450/90

=> b = 5 cm

Tādējādi trīsstūrveida pamatnes laukums ir,

A = (1/2) × b × h

= (1/2) × 5 × 10

= 25 kv.cm