- DFA attiecas uz deterministiskiem galīgiem automātiem. Deterministisks attiecas uz aprēķina unikalitāti. Galīgos automātus sauc par deterministiskiem galīgiem automātiem, ja iekārta nolasa ievades virkni pa vienam simbolam.
- Pakalpojumā DFA ir tikai viens ceļš konkrētai ievadei no pašreizējā stāvokļa uz nākamo stāvokli.
- DFA nepieņem nulles pārvietošanu, t.i., DFA nevar mainīt stāvokli bez ievades rakstzīmes.
- DFA var ietvert vairākus galīgos stāvokļus. To izmanto kompilatora leksiskajā analīzē.
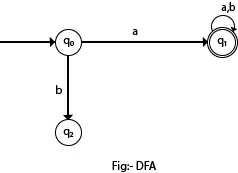
Nākamajā diagrammā redzams, ka no stāvokļa q0 ievadei a ir tikai viens ceļš, kas ved uz q1. Tāpat no q0 ir tikai viens ceļš ievadei b, kas dodas uz q2.
Formālā DFA definīcija
DFA ir 5 korpusu kolekcija, tāpat kā mēs aprakstījām FA definīcijā.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Pārejas funkciju var definēt šādi:
δ: Q x ∑→Q
DFA grafiskais attēlojums
DFA var attēlot ar digrāfiem, ko sauc par stāvokļa diagrammu. Kurā:
- Valsts tiek attēlota ar virsotnēm.
- Loka, kas apzīmēta ar ievades rakstzīmi, parāda pārejas.
- Sākotnējais stāvoklis ir atzīmēts ar bultiņu.
- Galīgo stāvokli apzīmē ar dubultu apli.
1. piemērs:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} Risinājums:
Pārejas diagramma:

Pārejas tabula:
| Pašreizējais stāvoklis | Nākamais statuss ievadei 0 | Nākamais 1. ievades stāvoklis |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
2. piemērs:
DFA ar ∑ = {0, 1} pieņem visu, kas sākas ar 0.
Risinājums:

Paskaidrojums:
- Iepriekš redzamajā diagrammā redzams, ka, ja ir dota 0 kā DFA ievade stāvoklī q0, DFA maina stāvokli uz q1 un vienmēr pāriet uz galīgo stāvokli q1, kad sākas ievade 0. Tā var pieņemt 00, 01, 000, 001... utt. Tā nevar pieņemt nevienu virkni, kas sākas ar 1, jo tā nekad nenonāks uz galīgo stāvokli virknē, kas sākas ar 1.
3. piemērs:
DFA ar ∑ = {0, 1} pieņem visus, kas beidzas ar 0.
Risinājums:

Paskaidrojums:
Iepriekš redzamajā diagrammā redzams, ka 0 kā DFA ievade stāvoklī q0, DFA maina stāvokli uz q1. Tas var pieņemt jebkuru virkni, kas beidzas ar 0, piemēram, 00, 10, 110, 100... utt. Tā nevar pieņemt nevienu virkni, kas beidzas ar 1, jo tā nekad nenonāks gala stāvoklī q1 1 ievadē, tāpēc virkne, kas beidzas ar 1, netiks pieņemta vai tiks noraidīta.
