Topoloģiskā šķirošana priekš Režisēts aciklisks grafiks (DAG) ir lineāra virsotņu secība, lai katrai virzītai malai u-v virsotne iekšā nāk pirms iekšā pasūtījumā.
Piezīme: Topoloģiskā kārtošana grafam nav iespējama, ja grafs nav a DIENA .
Piemērs:
Ieteicamā prakseDFS balstīts risinājums, lai atrastu topoloģisko šķirošanu jau ir apspriests.Ievade: Grafiks:
Piemērs
Izvade: 5 4 2 3 1 0
Paskaidrojums: Topoloģiskās šķirošanas pirmā virsotne vienmēr ir virsotne ar 0 grādu (virsotne bez ienākošām malām). Sekojošā grafika topoloģiskā šķirošana ir 5 4 2 3 1 0. Grafam var būt vairāk nekā viena topoloģiskā šķirošana. Vēl viena nākamā diagrammas topoloģiskā šķirošana ir 4 5 2 3 1 0.
Topoloģiskā secība var nebūt unikāla:
Topoloģiskā šķirošana ir atkarības problēma, kurā viena uzdevuma pabeigšana ir atkarīga no vairāku citu uzdevumu izpildes, kuru secība var atšķirties. Ļaujiet mums saprast šo jēdzienu, izmantojot piemēru:
Pieņemsim, ka mūsu uzdevums ir sasniegt mūsu skolu un, lai tur nokļūtu, mums vispirms ir jāsaģērbjas. Atkarības no apģērba valkāšanas ir parādītas zemāk esošajā atkarību grafikā. Piemēram, jūs nevarat valkāt apavus, pirms valkājat zeķes.
No iepriekš redzamā attēla jūs jau būtu sapratuši, ka pastāv vairāki veidi, kā ģērbties, zemāk esošajā attēlā ir parādīti daži no tiem.
java vesels skaitlis uz virkniVai varat uzskaitīt visa iespējamā topoloģiskā secība ģērbties atbilstoši iepriekšminētajam atkarības grafikam?
Algoritms topoloģiskās šķirošanas, izmantojot DFS:
Tālāk ir sniegts soli pa solim algoritms topoloģiskai šķirošanai, izmantojot pirmo dziļuma meklēšanu (DFS):
- Izveidojiet grafiku ar n virsotnes un m -virzītas malas.
- Inicializējiet kaudzīti un apmeklēto izmēru masīvu n .
- Katrai diagrammas neapmeklētajai virsotnei veiciet tālāk norādītās darbības.
- Izsauciet funkciju DFS ar virsotni kā parametru.
- Funkcijā DFS atzīmējiet virsotni kā apmeklētu un rekursīvi izsauciet DFS funkciju visiem neapmeklētajiem virsotnes kaimiņiem.
- Kad visi kaimiņi ir apmeklēti, uzspiediet virsotni uz kaudzes.
- Galu galā virsotnes ir apmeklētas, izvelciet elementus no steka un pievienojiet tos izvades sarakstam, līdz kaudze ir tukša.
- Iegūtais saraksts ir diagrammas topoloģiski sakārtotā secība.
Ilustrācijas topoloģiskās šķirošanas algoritms:
Zemāk redzamajā attēlā ir parādīta iepriekš minētās pieejas ilustrācija:

Kopējā topoloģiskās šķirošanas darbplūsma
1. darbība:
- Mēs sākam DFS no mezgla 0, jo tajā nav neviena ienākošā mezgla
- Mēs nospiežam mezglu 0 kaudzē un pārejam uz nākamo mezglu ar minimālo blakus esošo mezglu skaitu, t.i., mezglu 1.
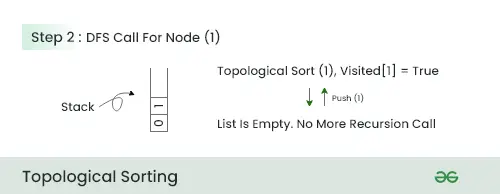
2. darbība:
- Šajā darbībā, jo šim mezglam nav blakus, iespiediet 1. mezglu kaudzē un pārejiet uz nākamo mezglu.
3. darbība:
- Šajā solī mēs izvēlamies mezglu 2, jo tam ir minimālais blakus esošo mezglu skaits pēc 0 un 1.
- Mēs izsaucam 2. mezgla DFS un nospiežam visus mezglus, kas tiek šķērsoti no 2. mezgla, apgrieztā secībā.
- Tātad nospiediet 3, tad nospiediet 2.
4. darbība:
- Tagad mēs saucam DFS mezglam 4
- Tā kā 0 un 1 jau ir stekā, mēs vienkārši nospiežam 4. mezglu kaudzē un atgriežamies.
sql izvēlieties no vairākām tabulām5. darbība:
- Tā kā visi blakus esošie 5. mezgli jau atrodas kaudzē, šajā darbībā mēs iespiežam 5. mezglu kaudzē un atgriežamies.
6. darbība: Šis ir pēdējais topoloģiskās kārtošanas solis, kurā mēs izvelkam visu elementu no kaudzes un izdrukājam to šādā secībā.
Tālāk ir aprakstīta iepriekš minētās pieejas īstenošana.
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, vektors & apmeklēja, kaudze & Stack) { // Atzīmēt pašreizējo mezglu kā apmeklētu apmeklēts[v] = true; // Atkārtot visām blakus esošajām virsotnēm for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Nospiediet pašreizējo virsotni uz steku, kas saglabā rezultātu Stack.push(v); } // Funkcija topoloģiskās kārtošanas veikšanai void topologicalSort(vector>& adj, int V) { kaudze Kaudze; // Sakraut, lai saglabātu rezultātu vektoru apmeklēts(V, false); // Izsauciet rekursīvo palīgfunkciju, lai saglabātu // Topoloģiskā kārtošana, sākot no visām virsotnēm pa vienam // pa vienam for (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> malas = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Grafiks attēlots kā blakus esošo saraksta vektors> adj(V); for (auto i : malas) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, Būla [] apmeklēts, Stack kaudze) { // Atzīmēt pašreizējo mezglu kā apmeklētu apmeklēts[v] = true; // Atkārtot visām blakus esošajām virsotnēm for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, visited, steck); } // Nospiediet pašreizējo virsotni uz steku, kas saglabā // rezultātu stack.push(v); } // Funkcija topoloģiskās kārtošanas veikšanai statiskā void topologicalSort(List> adj, int V) { // Salikt, lai saglabātu rezultātu kaudze = new Stack(); Būla [] apmeklēja = jauns Būla [V]; // Izsauciet rekursīvo palīgfunkciju, lai saglabātu // Topoloģiskā kārtošana, sākot no visām virsotnēm pa vienai // pa vienam for (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> malas = new ArrayList(); malas.add(Masīvi.asList(0, 1)); edges.add(Masīvi.asList(1, 2)); edges.add(Masīvi.asList(3, 1)); malas.add(Arrays.asList(3, 2)); // Grafiks attēlots kā blakus esošo sarakstu saraksts> adj = jauns ArrayList(V); for (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : malas) { adj.get(i.get(0)).add(i.get(1)); } topoloģiskā Kārtot(adj, V); } }>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] apmeklēja, Stack kaudze) { // Atzīmēt pašreizējo mezglu kā apmeklētu apmeklēts[v] = true; // Atkārtot visām blakus esošajām virsotnēm foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, steck); } // Nospiediet pašreizējo virsotni uz steku, kas saglabā // rezultātu steku. Push(v); } // Funkcija topoloģiskās kārtošanas veikšanai statiskā void TopologicalSort(List> adj, int V) { // Salikt, lai saglabātu rezultātu kaudze = jauns kaudze (); bool[] apmeklēts = jauns bool[V]; // Izsauciet rekursīvo palīgfunkciju, lai saglabātu // Topoloģiskā kārtošana, sākot no visām virsotnēm pa vienai // pa vienam for (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(steck.Pop() + ' '); } } // Draivera kods static void Main(string[] args) { // Mezglu skaits int V = 4; // Malu saraksts> malas = jauns saraksts>{ jauns saraksts {0, 1}, jauns saraksts {1, 2}, jauns saraksts {3, 1}, jauns saraksts {3, 2}}; // Grafs attēlots kā blakus esošo sarakstu saraksts> adj = jauns saraksts>(); for (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Saraksts i malās) { adj[i[0]].Pievienot(i[1]); } Topoloģiskā kārtošana(adj, V); } }>
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(steck.pop() + ' '); } } // Draivera kods (() => { // Mezglu skaits const V = 4; // Malu const malas = [[0, 1], [1, 2], [3, 1], [3, 2]] // Grafiks, kas attēlots kā blakus saraksts const adj = Array.from ({ garums: V }, () => []) { adj[i[0]] (i[1]); } topologicalSort(adj, V })();>>
Izvade Topological sorting of the graph: 3 0 1 2>
Laika sarežģītība: O(V+E). Iepriekš minētais algoritms ir vienkārši DFS ar papildu steku. Tātad laika sarežģītība ir tāda pati kā DFS
Palīgtelpa: O(V). Papildu vieta ir nepieciešama kaudzītei
filtrēšanas python
Topoloģiskā šķirošana, izmantojot BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Rādītājs uz masīvu, kurā ir // blakus saraksti public: Graph(int V); // Konstruktors void addEdge(int v, int w); // Funkcija malas pievienošanai grafikam void topologicalSort(); // izdrukā // visa grafika topoloģisko šķirošanu }; Grafs::Grafs(int V) { this->V = V; adj = jauns saraksts [V]; } void Graph::pievienotEdge(int v, int w) { adj[v].push_back(w); // Pievienojiet w v sarakstam. } // Funkcija topoloģiskās kārtošanas veikšanai void Graph::topologicalSort() { // Izveidojiet vektoru, lai saglabātu visu virsotņu vektoru pakāpē in_gree(V, 0); // Pārvietojiet blakus sarakstus, lai aizpildītu // virsotņu in_degree (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; for (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Pa vienai svītrot virsotnes no rindas un rindas // blakus esošās virsotnes, ja blakus esošās pakāpes vērtība kļūst par 0, kamēr (!q.empty()) { // Izvilkt rindas priekšpusi (vai izpildīt rindas noņemšanu) // un pievienot to topoloģiskā secība int u = q.front(); q.pop(); top_order.push_back(u); // Atkārtojiet visus blakus esošos mezglus // no rindas izslēgtā mezgla u un samaziniet to pakāpi // par 1 sarakstu ::iterators itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Ja in-gree kļūst par nulli, pievienojiet to rindai if (--in_gree[*itr ] == 0) q.push(*itr); skaitīt++; } // Pārbaudiet, vai ir bijis cikls if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Blakusparādību saraksts // grafika // attēlojums // Konstruktors Graph(int V) { this.V = V; adj = jauns ArrayList[V]; for (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = jauns LinkedList(); for (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = new ArrayList(); // Pa vienai rindas virsotnes izņem no rindas un // sarindo blakus virsotnes, ja // blakus esošās pakāpes kļūst par 0, kamēr (!q.isEmpty()) { // Izvilkt rindas priekšpusi un pievienot to // topoloģiskā secībā int u = q.poll(); topOrder.add(u); skaitīt++; // Atkārtojiet visus blakus esošos // izslēgtā mezgla u mezglus un samaziniet to pakāpi // par 1 for (int w : adj[u]) { // Ja pakāpe kļūst par nulli, pievienojiet to // rindai if (--inDegree[w] == 0) q.add(w); } } // Pārbaudiet, vai ir bijis cikls if (count != V) { System.out.println('Grafs satur ciklu'); atgriešanās; } // Drukāt topoloģisko secību priekš (int i : topOrder) System.out.print(i + ' '); } } // Draivera kods public class Main { public static void main(String[] args) { // Izveidojiet grafiku, kas norādīts iepriekš diagrammā Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println('Sekojošā ir dotā grafika topoloģiskā šķirošana'); g.topologicalSort(); } }> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Izvade
Grafa konstruēšanas laika sarežģītība ir O(V + E), kur V ir virsotņu skaits un E ir malu skaits.
Laika sarežģītība topoloģiskās šķirošanas veikšanai, izmantojot BFS, arī ir O(V + E), kur V ir virsotņu skaits un E ir malu skaits. Tas ir tāpēc, ka katra virsotne un katra mala tiek apmeklēta vienu reizi BFS šķērsošanas laikā.
Kosmosa sarežģītība:
Telpas sarežģītība grafa saglabāšanai, izmantojot blakus esošo sarakstu, ir O(V + E), kur V ir virsotņu skaits un E ir malu skaits.
Papildu vieta tiek izmantota virsotņu pakāpes glabāšanai, kam nepieciešama O(V) telpa.
BFS šķērsošanai tiek izmantota rinda, kurā var būt ne vairāk kā V virsotnes. Tādējādi rindas telpas sarežģītība ir O(V).
Kopumā algoritma telpas sarežģītība ir O(V + E), jo tiek glabāts grafiks, pakāpeniskais masīvs un rinda.
Rezumējot, sniegtās realizācijas laika sarežģītība ir O(V + E), un telpas sarežģītība arī ir O(V + E).
Piezīme: Šeit mēs varam izmantot arī masīvu, nevis steku. Ja tiek izmantots masīvs, izdrukājiet elementus apgrieztā secībā, lai iegūtu topoloģisko šķirošanu.
Topoloģiskās šķirošanas priekšrocības:
- Palīdz plānot uzdevumus vai notikumus, pamatojoties uz atkarībām.
- Atklāj ciklus virzītā grafikā.
- Efektīva, lai atrisinātu problēmas ar prioritātes ierobežojumiem.
Topoloģiskās šķirošanas trūkumi:
- Piemērots tikai virzītiem acikliskiem grafikiem (DAG), nav piemērots cikliskām diagrammām.
- Nevar būt unikāls, var pastāvēt vairāki derīgi topoloģiskie sakārtojumi.
- Neefektīvi lieliem grafikiem ar daudziem mezgliem un malām.
Topoloģiskās šķirošanas pielietojumi:
- Uzdevumu plānošana un projektu vadība.
- Atkarības risināšana pakotņu pārvaldības sistēmās.
- Kompilācijas secības noteikšana programmatūras veidošanas sistēmās.
- Strupceļa noteikšana operētājsistēmās.
- Kursu plānošana augstskolās.
Saistītie raksti:
- Kāna algoritms topoloģiskajai šķirošanai
- Visi virzīta acikliskā grafika topoloģiskie veidi