Prizmas virsmas laukums: Matemātikā prizma ir būtisks daudzskaldņu saimes loceklis, un to definē kā trīsdimensiju formu, kurā ir divi identiski daudzstūri, kas ir vērsti viens pret otru un ir savienoti ar taisnstūrveida vai paralelogrammu virsmām. Identiski daudzstūri var būt trīsstūri, kvadrāti, taisnstūri, piecstūri vai jebkurš cits n-šķautņu daudzstūris, un tos sauc par prizmas pamatnēm. Pārējās prizmas skaldnes ir paralelogrami vai taisnstūri.

Šajā rakstā mēs apspriedīsim dažāda veida prizmas un prizmu formulas virsmas laukums ar piemēriem un prakses problēmām.

Satura rādītājs

• Kāds ir prizmas virsmas laukums?
• Dažādi prizmu veidi
• Trīsstūrveida prizma
• Taisnstūra prizma
• Kvadrātveida prizma
• Piecstūra prizma
• Sešstūra prizma
• Prizmas formulas virsmas laukums
• Prizmas virsmas laukums Atrisinātie piemēri
• Praktizējiet problēmas uz prizmas virsmas

Kāds ir prizmas virsmas laukums?

Prizmas virsmas laukums tiek saukts par kopējo laukumu, ko aptver visas tās virsmas. Lai noteiktu prizmas virsmas laukumu, mums jāaprēķina katras tās skaldnes laukumi un pēc tam jāpievieno iegūtie laukumi. Prizmai ir divu veidu virsmas laukumi, proti, sānu virsmas laukums un kopējais virsmas laukums. Laukumu, ko aizņem prizmas virsmas, izņemot abas paralēlās virsmas (prizmas pamatnes), sauc par tās sānu virsmas laukumu.

Prizmas sānu virsmas laukums = [Pamatnes perimetrs × augstums] kvadrātvienības

Tagad prizmas kopējais virsmas laukums ir tās divu pamatu laukumu un sānu virsmas laukumu summa.

Vispārējā formula jebkura veida labās prizmas kopējās virsmas aprēķināšanai ir:

Prizmas kopējais virsmas laukums = [2 (bāzes laukums) + (pamatnes perimetrs × augstums)] kvadrātvienības

Dažādi prizmu veidi

Ir dažādi prizmu veidi, kuru pamatā ir prizmas pamatnes forma, piemēram,

• Trīsstūrveida prizmas,
• Kvadrātveida prizmas,
• Taisnstūra prizmas,
• Piecsstūru prizmas,
• Sešstūra prizmas,
• Astoņstūra prizmas.

Trīsstūrveida prizma

Prizmu ar trīsstūrveida pamatni sauc par trīsstūrveida prizmu. Trīsstūrveida prizma sastāv no trim slīpām taisnstūra virsmām un divām paralēlām trīsstūra pamatnēm. Pieņemsim, ka H ir trīsstūra prizmas augstums; a, b un c ir malu garums, un h ir trīsstūrveida pamatu augstums.

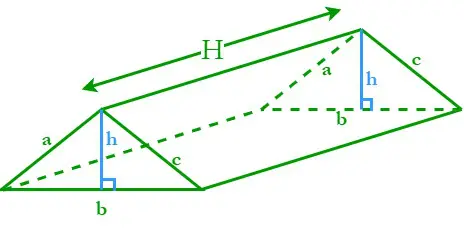
Trīsstūra pamatnes perimetrs (P) = tā trīs malu summa = a + b + c

Trīsstūrveida pamatnes laukums (A) = ½ × pamatne × augstums = ½ bh

Mēs zinām, ka vispārējā formula Taisnās prizmas sānu virsmas laukums ir L. S. A. = PH, kur P ir bāzes perimetrs un A ir pamatlaukums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam ,

Trīsstūrveida prizmas sānu virsmas laukums = (a + b +c)H kvadrātvienības

kur,

a, b, c ir trīsstūra pamatnes malas

H ir trīsstūrveida prizmas augstums

Mēs zinām, ka taisnās prizmas kopējās virsmas laukuma vispārējā formula ir T. S. A. = PH+2A, kur P ir bāzes perimetrs, A ir pamatlaukums un H ir prizmas augstums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam

Trīsstūrveida prizmas kopējais virsmas laukums = (a + b + c)H + 2 × (½ bh)

Trīsstūrveida prizmas kopējais virsmas laukums = (a + b + c)H + bh kvadrātvienības

kur,

a, b, c ir trīsstūra pamatnes malas

H ir trīsstūrveida prizmas augstums

h ir trīsstūra augstums

Taisnstūra prizma

Prizmu ar taisnstūra pamatni sauc par taisnstūra prizmu. Taisnstūra prizma sastāv no četrām taisnstūra virsmām un divām paralēlām taisnstūrveida pamatnēm. Lai prizmas augstums ir h un tās taisnstūra pamatnes garums un platums ir attiecīgi l un w .

Taisnstūra pamatnes perimetrs (P) = tā četru malu summa = 2 (l + w)

Taisnstūra pamatnes laukums (A) = garums × platums = l × w

Mēs zinām, ka taisnās prizmas sānu virsmas laukuma vispārējā formula ir L. S. A. = PH, kur P ir bāzes perimetrs un A ir pamatlaukums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam ,

Taisnstūra prizmas sānu virsmas laukums = 2h(l + w) kvadrātvienības

kur,

l ir garums

w ir platums

h ir augstums

Mēs zinām, ka taisnās prizmas kopējās virsmas laukuma vispārējā formula ir T. S. A. = PH+2A, kur P ir pamatnes perimetrs, A ir pamatlaukums un H ir prizmas augstums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam

Taisnstūra prizmas kopējais virsmas laukums = 2h(l + w) + 2(l × w)

= 2 lh + 2 wh + 2 lw

Taisnstūra prizmas kopējais virsmas laukums = 2 (lh + wh + lw) kvadrātvienības

kur,

l ir garums

w ir platums

h ir augstums

Kvadrātveida prizma

Prizmu ar kvadrātveida pamatni sauc par kvadrātveida prizmu. Kvadrātveida prizma sastāv no četrām taisnstūrveida virsmām un divām paralēlām kvadrātveida pamatnēm. Lai prizmas augstums ir h un tās kvadrātveida pamatnes garums ir s.

Kvadrātveida pamatnes perimetrs (P) = tā četru malu summa = s + s + s + s = 4s

Kvadrātveida pamatnes laukums (A) = (malas garums)²= s²

Mēs zinām, ka taisnās prizmas sānu virsmas laukuma vispārējā formula ir L. S. A. = PH, kur P ir bāzes perimetrs un A ir pamatlaukums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam,

Kvadrātveida prizmas sānu virsmas laukums = 4 kvadrātvienības

kur,

s ir kvadrātveida pamatnes puse

h ir kvadrātveida prizmas augstums

Mēs zinām, ka taisnās prizmas kopējās virsmas laukuma vispārējā formula ir T.S.A. = PH+2A, kur P ir bāzes perimetrs, A ir pamatnes laukums, un H ir prizmas augstums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam

Kvadrātveida prizmas kopējais virsmas laukums = [4sh + 2s ² ] kvadrātvienības

kur,

s ir kvadrātveida pamatnes puse

h ir kvadrātveida prizmas augstums

Piecstūra prizma

Prizmu ar piecstūra pamatni sauc par piecstūra prizmu. Piecstūra prizma sastāv no piecām slīpām taisnstūra virsmām un divām paralēlām piecstūra pamatnēm. Lai h ir piecstūra prizmas augstums; a un b ir piecstūra pamatņu apotēma garums un sānu garumi.

Piecstūra pamatnes perimetrs (P) = tā piecu malu summa = 5b

Piecstūra pamatnes laukums (A) = 5/2 x (apotēmas garums) x (malas garums) = 5ab

Mēs zinām, ka taisnās prizmas sānu virsmas laukuma vispārējā formula ir L. S. A. = PH, kur P ir bāzes perimetrs un A ir pamatlaukums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam,

Piecstūra prizmas sānu virsmas laukums = 5bh kvadrātvienības

kur,

b ir piecstūra pamatnes mala

h ir piecstūra prizmas augstums

Mēs zinām, ka taisnās prizmas kopējās virsmas laukuma vispārējā formula ir T. S. A. = PH+2A, kur P ir pamatnes perimetrs, A ir pamatlaukums un H ir prizmas augstums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam,

Piecstūra prizmas kopējais virsmas laukums = [5bh + 5ab] kvadrātvienības

kur,

b ir piecstūra pamatnes mala

a ir apotēma garums.

h ir piecstūra prizmas augstums

Sešstūra prizma

Prizmu ar sešstūra pamatni sauc par sešstūra prizmu. Sešstūra prizma sastāv no sešām slīpām taisnstūra virsmām un divām paralēlām sešstūra pamatnēm. Lai h ir sešstūra prizmas augstums; a ir sešstūra pamatņu sānu garumi.

Sešstūra pamatnes perimetrs (P) = tā sešu malu summa = 6a

Sešstūra pamatnes laukums (A) = 6 x (vienādmalu trīsstūra laukums)

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

Mēs zinām, ka taisnās prizmas sānu virsmas laukuma vispārējā formula ir L. S. A. = PH, kur P ir bāzes perimetrs un A ir pamatlaukums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam,

Sešstūra prizmas sānu virsmas laukums = 6ah kvadrātvienības

kur,

a ir sešstūra pamatnes puse

h ir sešstūra pamatnes augstums

Mēs zinām, ka taisnās prizmas kopējās virsmas laukuma vispārējā formula ir T. S. A. = PH+2A, kur P ir pamatnes perimetrs, A ir pamatlaukums un H ir prizmas augstums.

Aizvietojot visas vērtības vispārējā formulā, mēs iegūstam

Sešstūra prizmas kopējais virsmas laukums = [6ah +3√3a²] kvadrātvienības

kur,

a ir sešstūra pamatnes puse

h ir sešstūra pamatnes augstums:

Prizmas formulas virsmas laukums

Tālāk sniegtajā tabulā ir sniegta formula dažādu veidu prizmām:

Prizmas virsmas laukums Atrisinātie piemēri

1. uzdevums: Kāds ir prizmas augstums, kuras pamatlaukums ir 36 kvadrātvienības, pamatnes perimetrs ir 24 vienības un kopējā virsmas laukums ir 320 kvadrātvienības?

Risinājums:

Dotie dati,

Pamata platība = 36 kvadrātvienības

Bāzes perimetrs = 24 vienības

Prizmas kopējā virsmas laukums = 320 kvadrātvienības

Mums ir,

Prizmas kopējais virsmas laukums = (2 × pamatnes laukums) + (pamatnes perimetrs × augstums)

⇒ 320 = (2 × 36) + (24 × h)

⇒ 24h = 248 ⇒ h = 10,34 vienības

Tādējādi dotās prizmas augstums ir 10,34 vienības.

2. uzdevums: Atrodiet kvadrātveida prizmas kopējo virsmas laukumu, ja prizmas augstums un kvadrātveida pamatnes malas garums ir attiecīgi 13 cm un 4 cm.

Risinājums:

Dotie dati,

Kvadrātveida prizmas augstums (h) = 13 cm

Kvadrātveida pamatnes malas garums (a) = 4 cm

Mēs to zinām,

Kvadrātveida prizmas kopējais virsmas laukums = 2a²+ 4h

= 2 × (4)²+ 4 × 4 × 13

= 32 + 208 = 240 cm²

Līdz ar to dotās prizmas kopējā virsmas laukums ir 240 kv.cm.

3. uzdevums: nosakiet piecstūra prizmas pamatnes garumu, ja tās kopējā platība ir 100 kvadrātvienības un augstums un apotēmas garums ir attiecīgi 8 vienības un 5 vienības.

Risinājums:

Dotie dati,

Piecstūra prizmas kopējais virsmas laukums = 100 kvadrātvienības

Prizmas augstums (h) = 8 vienības

Apotēmas garums (a) = 5 vienības

Mēs to zinām,

Piecstūra prizmas kopējais virsmas laukums = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b (5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 vienības

Tādējādi bāzes garums ir 1,54 vienības

4. problēma: Nosakiet taisnstūra prizmas augstumu un taisnstūra prizmas kopējo laukumu, ja tās sānu virsmas laukums ir 540 kv.cm un pamatnes garums un platums ir attiecīgi 13 cm un 7 cm.

Risinājums:

Dotie dati,

Taisnstūra pamatnes garums (l) = 13 cm

Taisnstūra pamatnes platums (w) = 7 cm

Prizmas sānu virsmas laukums = 540 kv.cm

Mums ir,

Prizmas sānu virsmas laukums = bāzes perimetrs × augstums

⇒ 540 = 2 (l + w) h

⇒ 2 (13 + 7) h = 540

⇒ 2 (20) h = 540 ⇒ h = 13,5 cm

Mēs to zinām,

reliģiju saraksts

Taisnstūra prizmas kopējais laukums = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

= 2 × (91 + 94,5 + 175,5) = 722 kv. cm

Tādējādi dotās taisnstūra prizmas augstums un kopējais virsmas laukums ir attiecīgi 13,5 cm un 722 kv.cm.

5. uzdevums: nosakiet regulāras sešstūra prizmas virsmas laukumu, ja prizmas augstums ir 12 collas un pamatnes malas garums ir 5 collas.

Risinājums:

Dotie dati,

Prizmas augstums (h) = 12 collas

Pamatnes malas garums (a) = 6 collas

Regulāras sešstūra prizmas virsmas laukums = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3(5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 kv.collas

Tādējādi dotās prizmas virsmas laukums ir 489,9 kv.collas.

6. uzdevums. Aprēķiniet sānu un kopējo virsmas laukumu trīsstūrveida prizmai, kuras pamatnes perimetrs ir 25 collas, trijstūra pamatnes garums un augstums ir 9 collas un 10 collas, bet prizmas augstums ir 14 collas.

Risinājums:

Dotie dati,

Prizmas augstums (H) = 14 collas

Prizmas pamata perimetrs (P) = 25 collas

Trijstūra pamatnes garums = 9 collas

Trijstūra augstums = 10 collas

Mēs to zinām,

Prizmas sānu virsmas laukums = bāzes perimetrs × augstums

= 25 × 14 = 350 kvadrātcollas

Trīsstūrveida pamatnes laukums (A) = ½ × pamatne × augstums = 1/2 × 9 × 10 = 45 kv.col.

Trīsstūrveida prizmas kopējais virsmas laukums = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 kvadrātcollas

Tādējādi prizmas sānu un kopējās virsmas laukums ir attiecīgi 350 kv.collas un 440 kv.collas.

Praktizējiet problēmas uz prizmas virsmas

1. Dota taisnstūra prizma ar izmēriem:

• Garums = 6 cm
• Platums = 4 cm
• Augstums = 5 cm

Aprēķiniet kopējo virsmas laukumu.

2. Apsveriet trīsstūrveida prizmu ar izmēriem:

• Trijstūra pamatne = 8 cm
• Trīsstūra augstums = 6 cm
• Prizmas garums = 10 cm

Atrodiet kopējo virsmas laukumu.

3. Nosakiet regulāras piecstūra prizmas virsmas laukumu ar:

• Pamatnes sānu garums = 7 cm
• Prizmas augstums = 9 cm.

4. Aprēķiniet sešstūra prizmas virsmas laukumu ar:

• Parastās sešstūra pamatnes sānu garums = 10 cm
• Prizmas augstums = 12 cm.

Prismas virsmas laukums – FAQ

Kas ir prizma ģeometrijā?

Prizma ir trīsdimensiju forma ar divām kongruentām paralēlām pamatnēm un taisnstūrveida vai paralelogrammas sānu malām, kas tās savieno. Prizmām ir dažādas formas, piemēram, taisnstūra prizmas, trīsstūrveida prizmas un piecstūra prizmas, katrai no tām ir unikālas īpašības.

Kā atrast prizmas virsmas laukumu?

Lai atrastu prizmas virsmas laukumu, aprēķiniet visu tās skaldņu laukumus un pēc tam tos summējiet. Taisnstūra prizmai virsmas laukuma formula ir 2lw + 2lh + 2wh, kur l ir garums, w ir platums un h ir augstums. Citu veidu prizmām, piemēram, trīsstūrveida vai piecstūra prizmām, var būt nepieciešamas papildu formulas pamatlaukumam un sānu laukumam.

Kādas ir prizmas īpašības?

Prizmām ir vairākas galvenās īpašības:

• Viņiem ir divas kongruentas paralēlas bāzes.
• Visas sānu virsmas ir paralelogrammas.
• Augstums (augstums) ir perpendikulārs attālums starp abām bāzēm.
• Pamatnes pēc formas un izmēra ir identiskas.
• Pamatiem paralēlais šķērsgriezums vienmēr ir tādas pašas formas un izmēra kā pamatnēm.

Kādi ir prizmu reāli piemēri?

Prizmas var atrast dažādos ikdienas priekšmetos un konstrukcijās. Piemēri:

• Taisnstūra prizmas: ēkas, labības kastes, grāmatas.
• Trīsstūrveida prizmas: māju jumti, ķīļveida objekti.
• Piecstūras prizmas: daži kolonnu veidi, noteiktas arhitektūras struktūras.
• Sešstūra prizmas: noteikti kristālu veidi, daži iepakojuma konteineri.

Kāpēc virsma ir svarīga prizmās?

Virsmas laukumam ir izšķiroša nozīme prizmās, jo tas atspoguļo visu prizmas virsmu (virsmu) kopējo laukumu. Virsmas laukuma izpratne palīdz dažādos praktiskos pielietojumos, piemēram, aprēķinot materiāla daudzumu, kas nepieciešams prizmas formas objekta uzbūvēšanai vai pārklāšanai, siltuma pārneses ātruma noteikšanā un iepakojuma dizaina optimizēšanā.