Spēcīgi savienoti komponenti (SCC) ir grafu teorijas un algoritmu pamatjēdziens. Virzītā grafikā a Stingri savienots komponents ir virsotņu apakškopa, kurā katra apakškopas virsotne ir sasniedzama no katras citas virsotnes tajā pašā apakškopā, šķērsojot virzītās malas. Meklējot SCC diagramma var sniegt svarīgu ieskatu diagrammas struktūrā un savienojamībā ar lietojumiem dažādās jomās, piemēram, sociālo tīklu analīze, tīmekļa pārmeklēšana un tīkla maršrutēšana . Šajā apmācībā tiks izpētīta definīcija, rekvizīti un efektīvi algoritmi cieši saistītu komponentu identificēšanai grafiku datu struktūrās.

c++ pāris

Satura rādītājs

• Kas ir stingri savienoti komponenti (SCC)?
• Kāpēc stingri savienoti komponenti (SCC) ir svarīgi?
• Atšķirība starp savienotiem un stingri savienotiem komponentiem (SCC)
• Kāpēc parasto DFS metodi nevar izmantot, lai atrastu cieši saistītus komponentus?
• Divu cieši savienotu komponentu savienošana ar vienvirziena malu
• Brutāla spēka pieeja, lai atrastu cieši saistītus komponentus
• Efektīva pieeja cieši saistītu komponentu (SCC) atrašanai
• 1. Kosaraju algoritms:
• 2. Tarjana algoritms:
• Secinājums

Kas ir stingri savienoti komponenti (SCC)?

A cieši savienota sastāvdaļa virzīta grafa ir maksimālais apakšgrāfs, kurā katrs virsotņu pāris ir savstarpēji sasniedzams. Tas nozīmē, ka jebkuriem diviem mezgliem A un B šajā apakšgrafikā ir ceļš no A uz B un ceļš no B uz A.

Piemēram: Zemāk esošajā grafikā ir divi cieši saistīti komponenti {1,2,3,4} un {5,6,7}, jo tajā pašā cieši saistītā komponentā ir ceļš no katras virsotnes uz katru otro virsotni.

Stingri savienots komponents

Kāpēc stingri savienoti komponenti (SCC) ir svarīgi?

Izpratne par SCC ir ļoti svarīga dažādām lietojumprogrammām, piemēram:

• Tīkla analīze : Cieši savstarpēji saistītu mezglu kopu identificēšana.
• Tīmekļa rāpuļprogrammu optimizēšana : Tīmekļa diagrammas daļu noteikšana, kas ir cieši saistītas.
• Atkarības izšķirtspēja : Programmatūrā saprotot, kuri moduļi ir savstarpēji atkarīgi.

Atšķirība starp savienotiem un cieši savienotiem komponentiem ( SCC)

Savienojamība a nevirzīts grafiks attiecas uz to, vai divas virsotnes ir sasniedzamas viena no otras. Tiek uzskatīts, ka divas virsotnes ir savienotas, ja starp tām ir ceļš. Tikmēr Spēcīgi saistīts attiecas tikai uz virzīti grafiki . Virzīta grafa apakšgrāfs tiek uzskatīts par an Cieši saistīti komponenti (SCC) tad un tikai tad, ja katram virsotņu pārim A un B , pastāv ceļš no A uz B un ceļš no B uz A . Apskatīsim, kāpēc standarta dfs metode, lai atrastu savienotos komponentus grafikā nevar izmantot, lai noteiktu cieši saistītus komponentus.

Apsveriet šādu grafiku:

mysql pa kreisi pievienoties

Tagad sāksim a dfs zvaniet no 1. virsotnes, lai apmeklētu citas virsotnes.

Kāpēc parasto DFS metodi nevar izmantot cieši saistīto komponentu atrašanai?

Visas virsotnes var sasniegt no 1. virsotnes. Taču virsotnes 1 un 5,6,7 nevar atrasties vienā un tajā pašā cieši saistītā komponentā, jo nav virzīta ceļa no 5., 6. vai 7. virsotnes uz 1. virsotni. Grafam ir divi spēcīgi. savienotie komponenti {1,2,3,4} un {5,6,7}. Tāpēc parasto dfs metodi nevar izmantot, lai atrastu cieši saistītos komponentus.

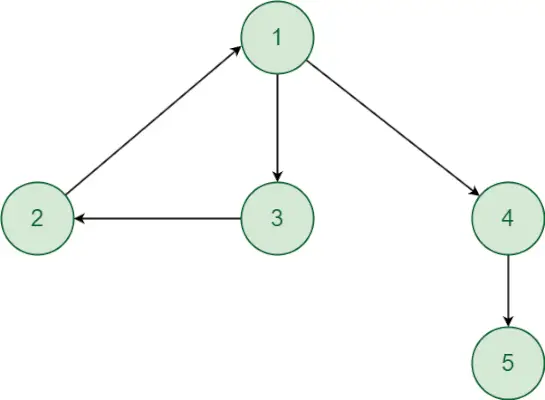
Divu cieši savienotu komponentu savienošana ar vienvirziena malu

Divas dažādas savienotas sastāvdaļas kļūst par vienu komponentu, ja tiek pievienota mala starp virsotni no viena komponenta līdz otra komponenta virsotnei. Bet tas tā nav stingri savienotos komponentos. Divas cieši savienotas sastāvdaļas nekļūst par vienu cieši saistītu komponentu, ja ir tikai vienvirziena mala no viena SCC uz otru SCC.

mākslīgais neironu tīkls

Brutāla spēka pieeja, lai atrastu cieši saistītus komponentus

Vienkāršā metode ir tāda, ka katrai virsotnei i (kas nav nevienas spēcīgas komponentes daļa) jāatrod virsotnes, kuras būs tā stipri saistītā komponenta daļa, kas satur virsotni i. Divas virsotnes i un j atradīsies vienā cieši saistītā komponentā, ja tām ir virzīts ceļš no virsotnes i uz virsotni j un otrādi.

Sapratīsim pieeju, izmantojot šādu piemēru:

• Sākot ar virsotni 1. Ir ceļš no 1. virsotnes uz virsotni 2 un otrādi. Līdzīgi ir ceļš no 1. virsotnes uz virsotni 3 un otrādi. Tātad virsotne 2 un 3 būs tajā pašā cieši saistītā komponentā kā virsotne 1. Lai gan ir virzīts ceļš no 1. virsotnes uz virsotni 4 un virsotni 5. Bet nav virzīta ceļa no virsotnes 4,5 uz virsotni 1, tāpēc virsotne 4 un 5 nebūs tajā pašā stingri savienotā komponentā kā virsotne 1. Tādējādi virsotne 1, 2 un 3 veido cieši savienotu komponentu.
• Virsotnei 2 un 3 jau ir noteikts stingri savienots komponents.
• Virsotnei 4 ir ceļš no 4. virsotnes uz 5. virsotni, bet nav ceļa no 5. virsotnes uz 4. virsotni. Tātad 4. un 5. virsotne neatradīsies vienā un tajā pašā cieši saistītā komponentā. Tātad gan Vertex 4, gan Vertex 5 būs daļa no Single Strongly Connected Component.
• Tādējādi būs 3 cieši saistīti komponenti {1,2,3}, {4} un {5}.

Tālāk ir aprakstīta iepriekš minētās pieejas īstenošana:

#include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, vektors & vis) { // Ja curr mezgls ir galamērķis return true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Lai noteiktu, vai ir ceļš no avota uz // galamērķa bool isPath(int src, int des, vektors>& adj) { vektors vis(adj.size() + 1, 0);  return dfs(src, des, adj, vis);  } // Funkcija, lai atgrieztu visas diagrammas cieši saistītās // komponentes.  vektors> atrast SCC(int n, vektors>& a) { // Saglabā visus cieši savienotos komponentus.  vektors> ans;  // Saglabā, vai virsotne ir daļa no jebkura Strongly // Connected Component vektora is_scc(n + 1, 0);  vektors> adj(n + 1);  for (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> malas { { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vektors> ans = obj.findSCC(V, malas);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>

import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, saraksts vis) { // Ja curr mezgls ir galamērķis return true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Lai noteiktu, vai ir ceļš no avota uz // galamērķis Būla isPath(int src, int des, List> adj) { Saraksts vis = jauns ArrayList(adj.size() + 1);  for (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> atrast SCC(int n, saraksts> a) { // Saglabā visus cieši savienotos komponentus.  Saraksts> ans = new ArrayList();  // Saglabā to, vai virsotne ir daļa no jebkura Strongly // Connected Component List is_scc = jauns ArrayList(n + 1);  for (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = new ArrayList();  for (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List mala : a) { adj.get(mala.get(0)).add(edge.get(1));  } // Pārbraucot visas virsotnes priekš (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = jauns ArrayList();  scc.add(i);  for (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> malas = new ArrayList();  edges.add(new ArrayList(saraksts(1, 3)));  edges.add(new ArrayList(saraksts(1, 4)));  edges.add(new ArrayList(saraksts(2, 1)));  edges.add(new ArrayList(saraksts(3, 2)));  edges.add(new ArrayList(saraksts(4, 5)));  Saraksts> ans = obj.findSCC(V, malas);  System.out.println('Stingri saistīti komponenti ir:');  priekš (Saraksts x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // Šo kodu ir sagatavojis shivamgupta310570>>Python

using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, saraksts vis) { // Ja curr mezgls ir galamērķis, atgriež true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } return false;  } // Lai noteiktu, vai ir ceļš no avota līdz galamērķim public bool IsPath(int src, int des, List> adj) { var parādīt = jauns saraksts (adj.Count + 1);  for (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> FindSCC(int n, saraksts> a) { // Saglabā visus cieši saistītos komponentus var ans = new List>();  // Saglabā to, vai virsotne ir daļa no jebkura cieši saistīta komponenta var isScc = new List (n + 1);  for (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  for (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } for (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Pievienot(i);  for (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> malas = jauns saraksts> { jauns saraksts {1, 3}, jauns saraksts {1, 4}, jauns saraksts {2, 1}, jauns saraksts {3, 2}, jauns saraksts {4, 5}};  Saraksts> ans = obj.AtrastSCC(V, malas);  Console.WriteLine('Stingri saistīti komponenti ir:');  foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // Šo kodu ir sagatavojis shivamgupta310570>>Javascript

Strongly Connected Components are: 1 2 3 4 5>

Laika sarežģītība: O(n * (n + m)), jo katram virsotņu pārim mēs pārbaudām, vai starp tām pastāv ceļš.
Palīgtelpa: O(N)

kā pārvērst no virknes uz int

Efektīva pieeja cieši saistītu komponentu (SCC) atrašanai

Lai grafikā atrastu SCC, mēs varam izmantot tādus algoritmus kā Kosaraju algoritms vai Tarjana algoritms . Izpētīsim šos algoritmus soli pa solim.

1. Kosaraju algoritms :

Kosaraju algoritms ietver divas galvenās fāzes:

1. Sākotnējā diagrammā tiek veikta pirmā dziļuma meklēšana (DFS). :
   • Vispirms veicam DFS oriģinālajā diagrammā un reģistrējam mezglu beigu laikus (t.i., laiku, kurā DFS pabeidz mezgla pilnīgu izpēti).
2. DFS veikšana transponētajā diagrammā :
   • Pēc tam mēs mainām visu grafa malu virzienu, lai izveidotu transponēto grafiku.
   • Pēc tam transponētajam grafikam veicam DFS, ņemot vērā mezglus dilstošā secībā pēc to pirmajā fāzē reģistrētajiem finiša laikiem.
   • Katrs DFS šķērsojums šajā fāzē mums dos vienu SCC.

Šeit ir vienkāršota Kosaraju algoritma versija:

1. DFS oriģinālajā diagrammā : ieraksta beigu laikus.
2. Transponējiet grafiku : apgriezt visas malas.
3. DFS transponētajā diagrammā : apstrādājiet mezglus saīsinātā beigu laika secībā, lai atrastu SCC.

2. Tarjāna algoritms :

Tarjana algoritms ir efektīvāks, jo tas atrod SCC vienā DFS caurlaidē, izmantojot steku un papildu grāmatvedību:

1. DFS šķērsošana : DFS laikā saglabājiet indeksu katram mezglam un mazāko indeksu (zemas saites vērtību), ko var sasniegt no mezgla.
2. Kaudze : sekojiet līdzi mezgliem, kas pašlaik atrodas rekursijas kaudzē (daļa no pašreizējā SCC tiek pētīta).
3. SCC identificēšana : Ja mezgla zemās saites vērtība ir vienāda ar tā indeksu, tas nozīmē, ka esam atraduši SCC. Izspiediet visus mezglus no kaudzes, līdz mēs sasniedzam pašreizējo mezglu.

Šeit ir vienkāršots Tarjana algoritma izklāsts:

1. Palaistindex>uz 0.
2. Katram neapmeklētam mezglam veiciet DFS.
   • Iestatiet mezgla indeksu un zemās saites vērtību.
   • Nospiediet mezglu uz kaudzes.
   • Katram blakus esošajam mezglam vai nu veiciet DFS, ja tas nav apmeklēts, vai atjauniniet zemās saites vērtību, ja tas ir kaudzē.
   • Ja mezgla zemās saites vērtība ir vienāda ar tā indeksu, izvelciet mezglus no steka, lai izveidotu SCC.

Secinājums

Izpratne un atrašana cieši savienotas sastāvdaļas virzītā grafikā ir būtiska daudziem datorzinātņu lietojumiem. Kosaraju's un Tarjāna algoritmi ir efektīvi veidi, kā identificēt SCC, un katram ir sava pieeja un priekšrocības. Apgūstot šos jēdzienus, jūs varat labāk analizēt un optimizēt sarežģītu tīklu struktūru un uzvedību.